Frågor och svar
NCM får då och då frågor från lärare och andra som besöker vår webbplats/känner till vår verksamhet. Vi publicerar här ett urval av frågorna och svaren. Allteftersom vi får nya frågor uppdateras spalten.
Se denna webbsida: http://ls.idpp.gu.se
Frågor om terminologi
8/21 – åtta tjugoendelar, åtta tjugoförstedelar eller åtta tjugoförstadelar?
13/41 – trettioen fyrtioandradelar, trettioen fyrtiotvådelar eller trettioen fyrtiotvåondelar?
Svar: Jag vet inte riktigt vad språkkonventionerna säger, men från en didaktisk synpunkt menar jag att det är bäst att säga åtta tjugoendelar eftersom det på det tydligast möjliga låter höra talet tjugoett. Man skulle rent av kunna säga åtta tjugoettdelar, eller i alla fall låta de som vill säga så.
I själva verket är den gängse bråkbenämningskonventionen lite olycklig, dvs att man tex säger tredje-del. Tredje är ju termen för ordningstalet medan tredjedel snarare har att göra med en uppdelning i tre stycken delar, dvs har att göra med antalet tre. Men detta kan vi knappast göra mycket åt.
En annan sak som jag alltid tar chansen att påpeka när den erbjuds. Bråktal, liksom decimaltal, är termer man aldrig bör använda. Ibland slinter även min tunga, men det är viktigt att hålla isär vad som är talområden, som t ex rationella tal eller reella tal, och vad som är representationsformer som t ex 1/4 eller 0.25. 0.25 och 1/4 är samma (rationella) tal (som även är ett reellt tal eftersom de reella tallen innehåller de rationella). 1/4 är dock skrivet (representerat) på bråkform och 0.25 på decimalform. Pi/6 är också skrivet på bråkform, men är inget rationellt tal.
En anekdot: När jag var lite lyssnade jag på Dan Hylander. Det fanns en låt som hette 21/3. Tjugoen tredjedelar. Jag tyckte det var ett skumt namn, särskilt när jag hade insett att 21/3 = 7. Inte förrän decennier senare när jag återigen hörde låten och lyssnade på texten insåg jag att 21/3 representerade vårens första dag, tjugoförsta mars, i Hylanders lyrik.
Ola Helenius
Svar: En omkrets är en längd (hos en sluten kurva, som t ex en cirkel eller rektangel). När man tänker på omkretsen som en längd (vilket är bra att man gör) så är det naturligt att säga att omkretsen är lång.
En längd anges dock med ett tal. När man pratar om tals storlek säger man aldrig lång. Däremot används ofta termen stor – ett stort tal. När man säger ”en stor omkrets” kan man dessutom mena att t ex den geometriska figuren som man refererar till är stor, på ett rent intuitivt plan. Så att säga en stor omkrets har så att säga en dubbelt relevant referens, till det underliggande geometriska objektet som man vill mäta omkretsen av, samt till talet som anger omkretsen.
Sammanfattningsvis skulle jag rekommendera att växelvis använda både stor och lång. Det är bra att använda stor i samband med att man poängterar själva kvantifieringen, dvs att omkretsen är ett tal. Det är bra att använda lång för anknyta till den geometriska aspekten: att det faktiskt är längden av en kurva som är det vi mäter.
Ola Helenius
Svar: Jag skulle vilja säga att båda uttrycken är korrekta. Tal är abstrakta men används ju för att beskriva olika saker och därför skapas vad vi kallar olika metaforer för tal.
När vi pratar om antal känns det naturligt att prata om små tal och stora tal för att vi tänker på små mängder och stora mängder.
När vi pratar om mätetal är det mer naturligt att prata om låga tal och höga tal eftersom vi kanske tänker på en skala där ett lågt värde är litet och ett högt är stort.
Tal kan därför både vara låga/höga och små/stora.
När man kommer in på negativa tal blir det ibland komplicerat med begreppen små och stora eftersom exempelvis -8 är mindre än -2 samtidigt som det är lätt hänt att det beskrivs som ett ”större negativt tal” eftersom absolutbeloppet är större (8>2). Då kan det vara mer begripligt att säga ett -8 är ett lägre tal än -2.
Det kan ju vara bra att hålla sig inom samma metafor vid samma tillfälle så att man inte ställer det lägsta värdet mot det största eller det minsta mot det högsta utan håller sig till jämförelsen:
lägsta/högsta eller minsta/största.
Cecilia Kilhamn
Fråga: Min fundering: I Tyskland (och även i andra länder) läses decimaltalet 3,14 som “tre komma ett fyra” och inte som “tre komma fjorton” som här i Sverige. Enligt min uppfattning så underlättar sättet jag lärde mig förståelsen för positionerna, t.ex. om man vill jämföra 3,7 med 3,14. Forskningen och erfarenheten visar att många elever i Sverige uppfattar att tre komma fjorton är större än tre komma sju (eftersom 14 > 7). Jag läste också om förslaget att läsa decimaltal med tiondelar och hundradelar, som 3,14 är tre och 1 tiondel och 4 hundradelar. Visserligen underlättar det förståelsen, men samtidigt är det rätt krångligt att läsa och jämföra decimaltal.
Jag hittade inget ställningstagande över att läsa decimaltal som jag lärde mig i Tyskland så jag är nyfiken på er åsikt. Kan eller bör man läsa decimaltal som 3,14 som tre komma ett fyra?
Svar: Det är en intressant fråga du lyfter. Man ser ofta varningar för att säga exempelvis ”tre komma fjorton”, och med all rätt. Precis som du skriver är det en väldokumenterad missuppfattning som kan uppstå. I ett första inlärningsskede föreslås därför att man, som du också påpekar, säger ”tre hela, en tiondel och fyra hundradelar” för att betona vad det är för talsorter man har. Detta blir krångligt att fortsätta med och då finns det två vägar att gå. Antingen att uttala varje siffra för sig: ”tre komma ett fyra”, eller att sätta samman decimalerna och uttala dem som en klump: ”tre komma fjorton”.
I Sverige är vi inte konsekventa. Fråga en som har lärt sig många decimaler på pi så kommer du att se att hen tar en siffra i taget. Ingen skulle utläsa 3,14592 som ”tre komma fjortontusenfemhundranittiotvå”. Nej, så fort det blir mer än tre decimaler skulle jag nog vilja säga att vi, även i Sverige, uttalar varje siffra för sig. Ett intressant fenomen är också att vi har en tendens att gruppera siffrorna två och två. Många skulle utläsa 3,1415 som ”tre komma fjorton femton”. Vad det beror på vet jag inte, men det är samma fenomen som med telefonnummer, där de flesta säger siffrorna parvis.
Är det två decimaler (och ibland tre) utläser vi dem alltså ofta ihop eller parvis.
Nu gissar jag bara, men jag tror att det finns en förklaring till varför vi gör så. I Sverige är matematiken av tradition ett tillämpat ämne. Fokus i läroplanen är mer på användning av matematik än på matematik som abstrakt vetenskap. Även i högre utbildning syns denna tendens. Vid Göteborgs universitet är institutionen för matematiska vetenskaper ett samarbete med Chalmers tekniska högskola. Matematik, som på antikens tid var ett filosofiskt ämne, betraktas här som ett tekniskt ämne. Vad spelar det för roll då?
Jo, i alla tillämpningar representerar tal ofta mätvärden, där vi vanligtvis växlar till en mindre enhet när det blir mindre än en hel.
Exempelvis är 3,14 meter detsamma som 3 meter och 14 centimeter. 3,14 kronor är 3 kronor och 14 öre.
Jag skulle kunna tänka mig att det är den här användning av decimaltal som ligger bakom att det känns mer naturligt att säga som vi gör.
En annan förklaring kan manhitta om man tittar i gamla skolböcker där decimaltal infördes som decimalbråk. I en bok från 1916 hittar jag exempelvis många uppgifter av den här typen:
Teckna med användning av decimalkomma:
45 tiondelar
63 hundradelar
875 hundradelar
55 tusendelar
4 367 tusendelar
Jag tror att det är viktigt att man vet vad det är för sorts tal man har att räkna med och att man kan omvandla mellan talsorter.
0,14 kan utläsas som ”en tiondel och fyra hundradelar” eller som ”fjorton hundradelar”. Vill man säga hur många tusendelar det är blir det 0,140 det vill säga ”etthundrafyrtio tusendelar.” I det sammanhanget är det rimligt att säga att det är ”noll komma fjorton hela”.
Efter denna långa utläggning kommer jag fram till att det inte finns ”ett rätt sätt” att säga decimaler på utan att det beror på situationen hur vi gör. En bra ingång i undervisningen är därför att be eleverna uttrycka samma tal på olika sätt. När det handlar om enhetslösa tal, som exempelvis pi, skulle jag själv föredra att säga ”tre komma ett fyra”. Har jag många decimaler skulle jag absolut göra det.
Cecilia Kilhamn
Svar: Termer för matematikundervisning – ett stödmaterial för undervisning i matematik och studiehandledning på olika språk. skolverket.se/skolutveckling/inspiration-och-stod-i-arbetet/stod-i-arbetet/resurser-for-undervisning-i-modersmal
Fråga:
Term + term = summa
Term – term = differens
Men vad kallas ”svaret” om man blandar räknesätten?
Svar:
Du ställer en bra och relevant fråga.
I boken Matematiktermer i skolan av Kiselman och Mouwitz står det så här:
summa
definition
resultat av en addition
kommentar
Termen summa används även för additionsuttrycket eller för ett kombinerat additions- och subtraktionsuttryck.
Man använder alltså ordet summa om det finns flera termer i en additiv struktur.
Jag skulle tro att förklaringen hänger samman med hur räknesätten definieras rent matematiskt där subtraktion är en del av en additiv struktur och kan definieras som addition av inversen: 7 – 3 = 7 + (-3)
På samma sätt kan man säga produkt om ett multiplikationsuttryck även när det innehåller en division eftersom divisionen kan ses som en multiplikation med inversen: 6 · 7 / 2 = 6 · 7 · ½
// Cecilia Kilhamn
Fråga: På min skola har jag ofta hört lärare säga till eleverna, “Ni ska skriva ner ett tal där svaret blir 2.”
Jag har lagt märke till att många elever blir förvirrade när de hör lärare säga att ett “tal” är något som består av siffror, samtidigt som de lär sig om begrepp som jämna tal, udda tal, hela tal, och så vidare. Eleverna förväntas kunna skriva ner ett “tal” där svaret är 2, vilket kan skapa förvirring eftersom till exempel talet 103 inte ger svaret 2.
Hur bör lärare formulera sig under matematikundervisningen för att undvika denna förvirring? Ska man använda ordet “tal” i olika sammanhang med två olika betydelser, eller finns det ett bättre sätt att kommunicera dessa begrepp?
Svar: Svaret är enkelt. Lärare bör inte använda termen ”tal” när det refererar till en uppgift, t ex en uppgift i boken (trots att det i det ibland görs så i vardagsspråk). Som du skriver är det gravt förvirrande för eleverna.
Det är mycket bättre att vara terminologiskt specifik och fråga efter det man är ute efter. Till exempel:
- Skriv en beräkning med svaret 2
- Skriv en addition med svaret 2
- Skriv en subtraktion med svaret 2
- Skriv ett uttryck som innehåller alla fyra räknesätt och som är lika med 2.
- Beskriv en händelse som leder till en beräkning med svaret 2.
- Hitta på en uppgift med svaret 2.
Frågor om undervisningsmetodik och material
Svar: Idag finns en hel del att läsa på svenska. Jag känner inte till vem som arbetar med det i skolorna, men jag kan hjälpa dig på traven med en del att läsa.
Tidigare arbetade jag i lärarutbildningen och där bildade vi en grupp som arbetade med vad vi kallade ROMB (Reflekterande Och Matematiserande Barn). Vi genomförde ett tvåårigt projekt där vi testade en hel del av Mathematics in the Citys saker i svensk kontext. Vi skrev ett antal Nämnaren artiklar om arbetet, se länkar längst ner. De personer som arbetade med ROMB var förutom mig även Britt Holmberg, Christina Skodras och Susanne Frisk. Om du vill kontakta någon som fortfarande har kurser med dessa inslag i lärarutbildningen föreslår jag att du kontaktar Christina Skodras.
En fortsättning på ROMB blev ett kursutvecklingsprojekt där vi försökte omsätta en del av de idéer vi fått oss till dels genom MitC. Detta projekt resulterade i en hel del nya inslag i våra kurser i lärarutbildningen och en bok med titel Matematiska samtal i klassrummet – vägar till elevers lärande, liber.se/produkt/matematiska-samtal-i-klassrummet.
Under denna tid har vi också översatt en hel del material från MitC som nu finns på svenska och i viss mån anpassat till svensk skola.
Dessa böcker är utgivna av Studentlitteratur i en serie som kallas Unga matematiker i arbete. Där finns tre huvudböcker som behandlar undervisning i åk F-6 (främst taluppfattning och aritmetik och lite algebra). Dessutom finns två temaområden med direkt lektionsplaneringar översatta: T-shirtfabriken och Organisera och inventera.
Eftersom jag är ganska inspirerad av MitC själv har jag låtit en hel del av deras idéer komma med i de texter jag skrivit för skolverkets moduler. Vi håller på med en revidering av modulerna för Taluppfattning och tals användning. Texterna för åk 1-3 finns tillgängliga, övriga kommer till vårterminen 2022. Du hittar till exempel en text som tar upp lärandelandskapet redan i del 1.
I flera av de andra delarna återkommer andra delar, exempelvis serier sammanlänkade uppgifter, så kallade ”strings”, och användning av modeller såsom tallinjen och rektanglar i undervisningen.
Jag hoppas att detta kan inspirera dig att arbeta vidare. Om du hittar några kollegor att arbeta tillsammans med skulle jag rekommendera ett ni tillsammans börjar med att läsa den första huvudboken.
Nämnarenartiklar:
ncm.gu.se/wp-content/uploads/2020/07/1319_16_2.pdf
ncm.gu.se/wp-content/uploads/2020/07/0812_16_4.pdf
ncm.gu.se/wp-content/uploads/2020/07/0914_16_3.pdf
ncm.gu.se/wp-content/uploads/2020/07/1317_18_1.pdf
ncm.gu.se/wp-content/uploads/2020/07/1414_19_2.pdf
ncm.gu.se/wp-content/uploads/2021/03/3541_19_4.pdf
ncm.gu.se/wp-content/uploads/2021/03/0712_20_1.pdf
Cecilia Kilhamn
Fråga: Vi är några lärare som sitter och utvärderar elevernas resultat av testerna Förstå och använda tal. Vi märker att våra elever succesivt från åk 7 till åk 9 blir sämre och sämre på den sista delen som handlar om skriftliga beräkningar av de fyra räknesätten.
Vi vet att eleverna tränar mycket uppställning i åk 4 – 6 medan vi i åk 7 – 9 oftast låter våra elever använda miniräknare vid liknande beräkningar.
Vi dumförklarar kanske oss själva nu 🙂 men borde vi låta eleverna fortsätta träna uppställningar? På vilket sätt ökar det elevernas taluppfattning? Alltså varför har ni valt att ha med dem i testet? Det vi ser av elevernas svar är att de försöker komma ihåg metoderna för de fyra räknesätten, men lyckas inte. Kikar man på gamla nationella prov åk 6 så ser man att de också lägger stor vikt vid att eleverna ska kunna just metoderna för uppställning. Vad är det vi missar som ni ser?
Vi är medvetna om att eleverna i Förstå och använda tal inte måste använda uppställningar, men det är trots allt det som de försöker göra eftersom det är så viktigt på mellanstadiet.
Svar: Era frågor är rätt djupa, faktisk och berör flera av de komplexiteter som är associerade med skolmatematiken och dess undervisning och lärande. Jag ska försöka dela upp frågan i vissa delfrågor och besvara dem var för sig.
1. Behöver elever kunna utföra beräkningar med de fyra räknesätten för hand?
Den här frågan kan man se från två håll. Dels kan man försöka kolla vad kursplanen säger. Där nämns för 7-9 hududräkning och skriftlig beräkning. Visserligen specificeras tal i bråk- eller decimalform, men här tycker jag att det i decimalform också är rimligt att inkludera (flersiffriga) heltal. Redan för 4-6 nämns ju också explicit metoder för beräkningar (med de fyra räknesätten) med naturliga tal och det vore orimligt att anta att eleverna inte längre ska kunna detta.
Men en delvis annan fråga är varför det testas i Förstå & använda tal (FAT) som ju inte i första hand är framtagen för att testa det som våra kursplaner specificerar utan det som rent allmänt är viktiga kunskaper inom den grundläggande aritmetiken. Men även här är helt enkelt slutsatsen att vissa matematiska egenskaper som utnyttjas vid beräkningar faktiskt är så viktiga att de bör vara med. Om man analyserar uppgifterna i testerna 7, 8 och 9 (de sista i varje test) som detta gäller så ser man att alla faktiskt går att hantera med kunskap om positionssystemet och vissa andra saker som t ex distributiva lagen. Talen i uppgifterna är valda så att sådana resonemang ska fungera. Naturligtvis kan man även lösa dem med standardalgoritmer (och då räcker det att man kan algoritmerna) men det är inte nödvändigt, exakt som ni själva redan har observerat.
2. Varför blir era elever sämre?
Även detta har ni ju i princip redan svarat på själva, så jag ska bara bena ut det lite till. De blir sämre för att ni inte undervisar dem i de kunskaper som man behöver för att med säkerhet hantera de uppgifter det gäller. De får inte stöd i att underhålla och befästa de kunskaper de har, eftersom de istället för använda räknare. Då är det självklart att de kommer att bli sämre. Det är en missuppfattning att man kommer ihåg saker om man en gång har lärt sig det ordentligt, så även många av de som en gång var säkra på den här sortens uppgifter (lösta med uppställningar eller på anat sätt) kommer helt enkelt att glömma.
3. Så hur ska ni göra då?
Om man accepterar punkt 1 (och 2) så blir slutsatsen att ni är behöver undervisa om lösning av den här sortens beräkningsuppgifter. Man kan välja att fortsätta att undervisa om uppställningarna eller fokusera på andra metoder eller båda och. Jag tror personligen inte alls att det räcker att låte eleverna träna. De som kommer till er med bra kunskaper i detta kanske klarar att upprätthålla dem om de får träna på det ibland, men det kommer inte att hjälpa de andra. Det måste (som vanligt) till specifik undervisning.
Mitt förslag skulle vara att då och då ha specifika pass om detta och dela upp dem i två kategorier. För algoritmerna skulle jag (lite kontroversiellt kanske) fokusera på att kunna utföra dem snabbt och helt utan fel. Inte genom att träna på massor med exempel utan genom att specifikt träna på ”inställningen”, dvs arbeta med metakognitiva strategier för hur man ska tänka när man väljer att ställa upp och utföra en uppställning. Det här tror jag ska utföras i helklass kombinerat med smarta gruppindelningar där Ala jobbar med samma uppgift och där fokus är ”hur kan jag lösa denna med en uppställning och vara HELT säjer på att jag gör rätt”. Den här undervisningen bör rimligen inkludera att gå igenom de vanligaste feltyperna för varje uppställning. Om man undantar elever som överhuvudtaget har svårt att följa och tillgodogöra sig undervisningen (kan vara olika skäl) så finns det enligt den kunskap jag har (efter at ha läst forskning om matematiksvårigheter) huvudsaken en kategori som kan ha svårt att bli säker på uppställningar och det har med vissa svagheter i den visuospatiella precisionen att göra. Det är helt enkelt svårt att skriva rätt saker på rätt ställen. Men även för dessa tor jag att det hjälper med den metakognitiva strategi som jag stakade ut ovan.
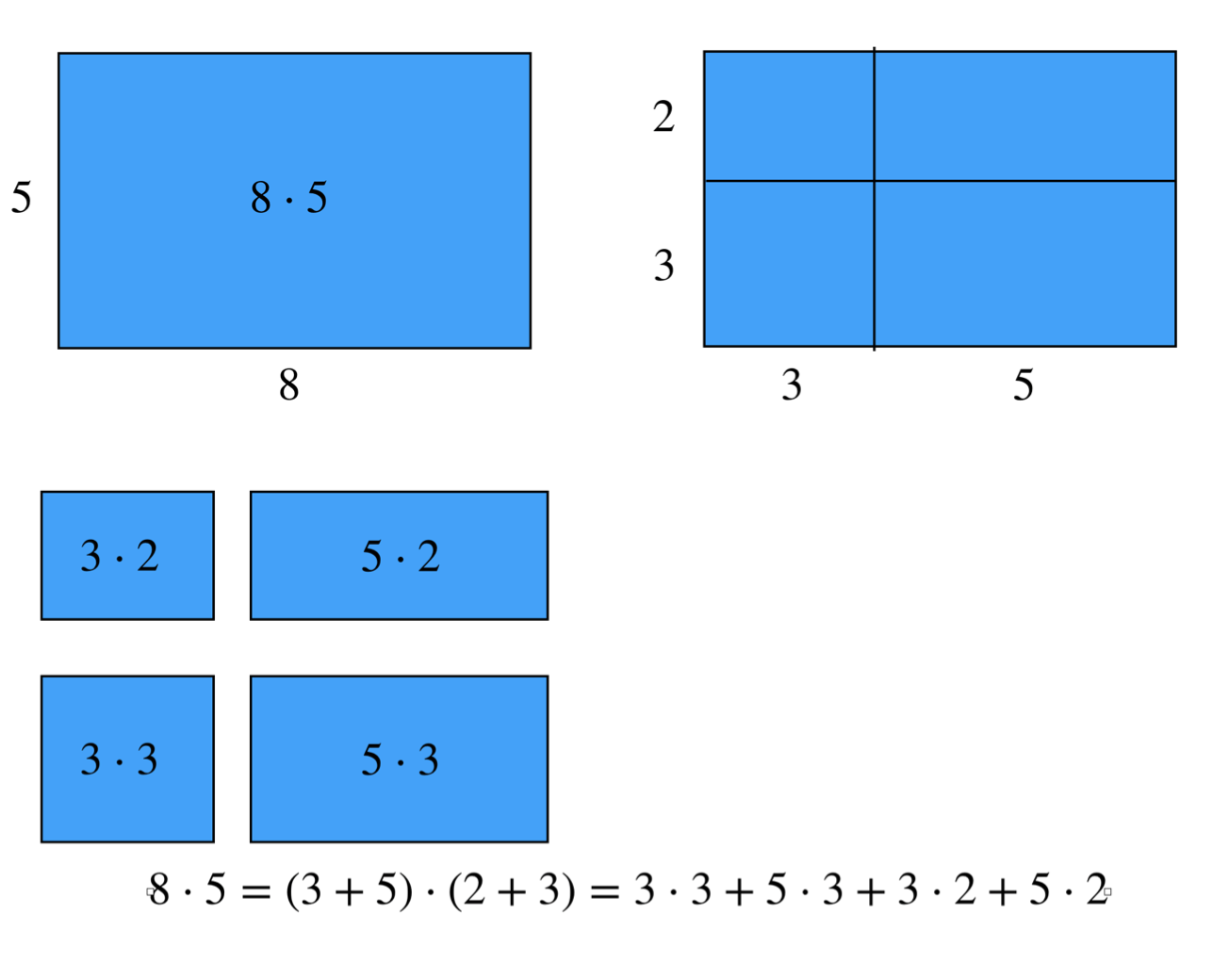
Den andra kategorin handlar om att undervisa ”själva talupfattningen”, dvs förbereda för att kunna lösa den typ av beräkningar den handlar om genom resonemang. I praktiken handlar det då om två saker. Dels positionssystemet, dvs hur man bryter isär saker i tiotal och ental etc. För addition och subtraktion är det här huvudsakligen det enda. Positionssystemets operationella egenskaper, kan man säga. För övrigt är standarduppställningarna för addition och subtraktion i praktiken direkt a tillämpningar av positionssystemet. Det är alltså en meningsull taluppfatningsuppgift att analysera varför algoritmerna funkar. För multiplikation och division tillkommer också distributiva lagen. Det är den som gör att man kan beräkna 5*23 som 5*20+5*3 och 35*23 som 30*20+30*3+20*5+5*3. Multiplikationsalgoritmen är en tillämpning av detta, men inte bara. Den är mycket mer intrikat och i min mening är det inte särskilt meningsfullt att analysera den. Det är bättre på att fokusera direkt på tillämpning av distributiva lagen, möjligen med hjälp av areamodeller som stöd (se bild). Ett själv till det är att distributiva lagen är oerhört viktig även när man arbetar med algebra, så ju bättre man är på att resonera med den, desto enklare får man det med algebran framöver. I denna andan kan man alltså med fördel koppla ihop undervisningen om resonemangsbaserade lösningsmetoder för flersiffriga multiplikationsupgifter med undervisningen i algebra om distributiva lagen och dess tillämpningar.
Som en liten extra utvikning:
Distributiva lagen är i sig en elementär observation som man får ut följande bild (bilaga, gröna rutorna). Dessa två rektanglar (när de sitter ihop) är 5*8 och när de är isärklippta 5*3+5*5. Man kan göra så för att 8=3+5. Om vi vll kunna skriva 8 gånger 3+5 utan missförstod måste vi införa parenteserna, lite som att vi ringar in 3+5 för att markera att det ännu ska betraktas som en sak som ska multipliceras med 5. När väl denna notation är införd har vi direkt 5*(3+5)=5*3+5*5. Och rent allmänt om vi ska betrakta a*m kan vi för varje tänkbar uppdelning additiv av m som m=b+c på samma sätt få a(b+c)=ab+ac.
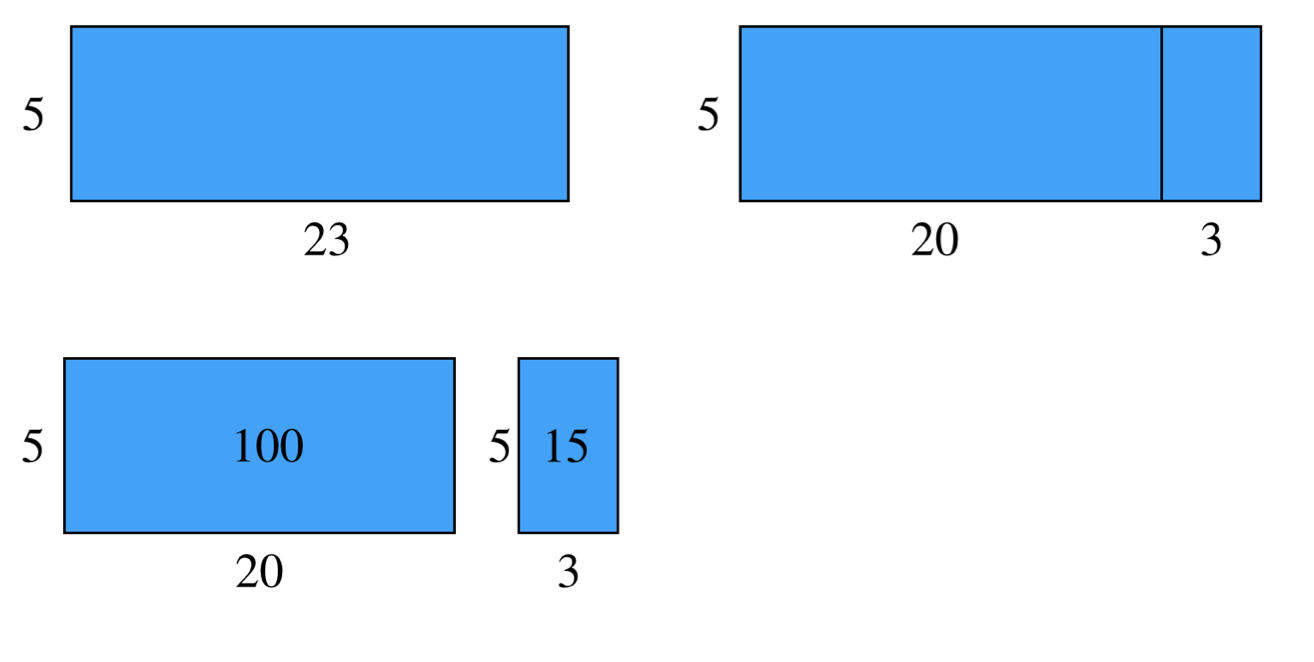
Tillämpat på när man delar upp i tiotal och ental 23=20+3 har man sedan en grafisk illustration av den konceptuella modellen för hu distributiva lagen och positionssystemet tillsammans ger oss sätt att beräkna multiplikationer flersiffriga tal (bifogad fil 2) och sedan kan man utvidga detta till när man delar upp båda faktorerna (fil 3) osv. Detta känner ni säkert till, men även om sånt här ibland undervisas bra redan på lågstadiet, så måste man också påminna om det, dvs undervisa om det, även på högstadiet om det ska eleverna ska kunna rycka fram minnena av det vid behov.
Ola Helenius
Svar:
Det finns flera olika sätt att introducera detta, delvis beroende på om du utgår från bråk eller om du utgår från decimaltal och vilka förkunskaper eleverna har. Att använda en areamodell eller rektangelmodell för multiplikation upplevs ofta ett som ett konkret sätt – då ses inte multiplikation som upprepad addition utan som en area. Utgår man från bråk är skalning och proportionellt tänkande ett annat sätt att tänka på.
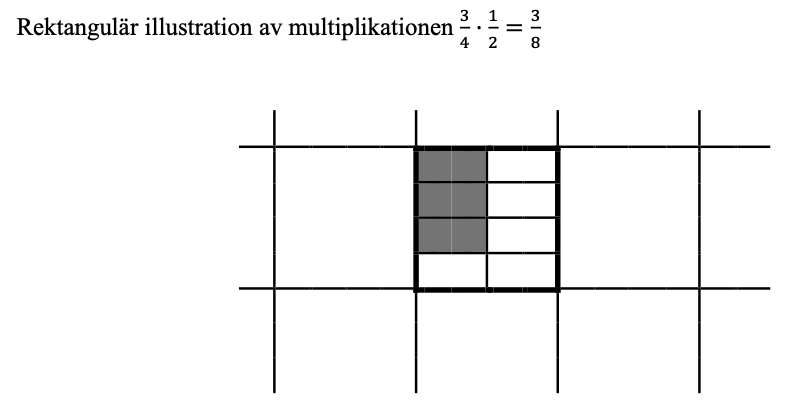
Rektangelmodellen illustreras exempelvis så här där en stor kvadrat är 1 areaenhet (I decimalform skulle bilden motsvara 0,75 · 0,5):
En representation av multiplikationen 0,3 · 0,7 kan se ut så här där den stora kvadraten är en areaenhet och sidorna är delade i tiondelar:
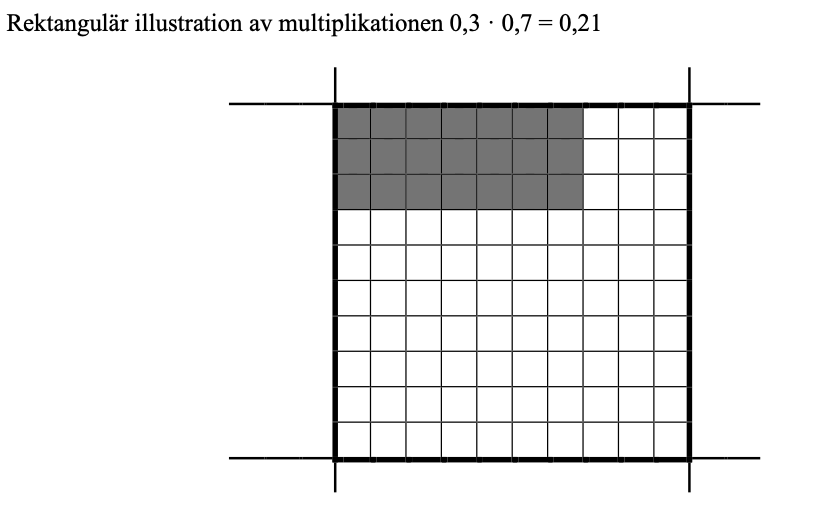
Läs om rektangelmodellen i den här texten på Lärportalen (.docx) där bilderna är hämtade.
Om eleverna inte är alls vana vid att se multiplikation som area kan det vara bra att introducera modellen med heltal först. Andra texter som visar hur rektangelmodellen fungerar finns i Nämnaren:
Petersson, J. (2013). Multiplikation i rutnät. Nämnaren 2016(2), 24–28.
ncm.gu.se/pdf/namnaren/2428_16_2.pdf
Skodras, C. (2016). Muffles’ truffles. Undervisning i multiplikation med systematiskt varierade exempel. Nämnaren 2016(2), 13–19.
ncm.gu.se/pdf/namnaren/1319_16_2.pdf
Dunkels, A. (1988). Multiplikation i åk 3 – glimtar från ett undervisningsexperiment. Nämnaren, 15(2), 47–54.
ncm.gu.se/pdf/namnaren/4754_88_2.pdf
Med vänliga hälsningar
Cecilia K
Svar 12 januari 2024
Språkutvecklande arbete i matematik kan ha olika syfte.
1) Syftet kan vara att använda matematiklektioner för att stärka elevens språkutveckling generellt. Det är ett vanligt syfte när det finns många elever med svenska som andra språk i klassen. Om detta är syftet finns det inspiration att hämta från mer generella kunskapsfält kring flerspråkiga elever. Bland annat har Skolverket mycket information (googla: Skolverket flerspråkighet)
Petra Svensson Källberg, Eva Norén och Ulrika Ryan är tre forskare som tittar på flerspråkighet just i relation till matematik. De är verksamma i ett nationellt lärar- och forskarnätverk med namnet Språk, kultur och matematik, som de berättar om i en artikel i Nämnaren 2022:3.
2) Syftet kan vara att utveckla elevernas matematiska språk och förmåga att kommunicera i matematik. Detta syfte bör alltid vara en del av matematikundervisningen eftersom den handlar om alla elevers förmåga att hantera matematikens språk. Matematikens ämnesspecifika språk innehåller fler delar som alla behöver belysas i undervisningen.
a) specifika matematikord och hur de används,
b) matematiska symboler och hur de används,
c) matematikens syntax, dvs hur man i matematiken sätter samman ord och symboler för att skapa mening. En sak som skiljer matematiskt språk från exempelvis vardagsspråk är att det är kort och stringent och söker en logisk uppbyggnad. Sambandsord (ibland ersatta av symboler såsom implikationspilar) är viktiga för att skapa logisk följd i argumentationen. För att utveckla förmågan att föra matematiska resonemang och argumentera logiskt behöver man sätta fokus på hur språket används i just matematik. www.su.se/polopoly_fs/1.129169.1363795732!/menu/standard/file/Sambandsord.pdf
d) andra matematiska uttrycksformer såsom tabeller och grafer. Matematiken är abstrakt till sin karaktär och många matematiska begrepp är därför helt beroende av sina skriftliga representationer.
Moduler
Om en lärare eller ett lärarlag vill få inspiration till att arbeta språkutvecklande i matematik kan vi rekommendera de moduler för Språk i matematik som finns på Skolverkets lärportal. Dessa reviderades 2021 och innehåller både aktuella texter och aktiviteter. Tanken med modulerna är att de ska fungera som fortbildningsmaterial för kollegialt utvecklingsarbete i studiecirkelformat som sträcker sig över en eller två terminer med avsatta kollegiala träffar. Men det är givetvis ingenting som hindrar att vissa delar lyfts ut eller bara vissa texter läses. Det finns tre moduler: Språk i matematik F-3; 4-6; 7-9
larportalen.skolverket.se
larportalen.skolverket.se/moduler?focusArea=Matematik
Nämnaren
En annan inspirationskälla är artiklar skrivna för Nämnaren. På webben kan man söka artiklar i fulltextsdatabasen och hitta en massa intressant.
ncm.gu.se/namnarenopenaccess-sok
För den som vill ha något att börja med rekommenderar vi särtrycket med artiklar om just Matematik och språk som togs fram 2022 och som går att köpa på NCM.
Bok-tips
Andra böcker vi kan tipsa om är:
Kilhamn, C., Nyman, R., Knutsson, L., Holmberg, B., Frisk, S., Skodras, C., & Gallos Cronberg, F. (2019). Matematiska samtal i klassrummet. Liber
Atkins, S. L. (2019). Att skapa en språkrik matematikundervisning. Studentlitteratur
Frågor om geometriundervisning
Svar: När det gäller bilder så är det en vanlig situation i matematisk modellering att bilder inte är skalenliga. Eftersom man inledningsvis inte vet hur bilden kommer att se ut kan man inte rita en skalenlig bild. Men för att kunna tänka kring uppgiften behöver man ofta rita en bild och då blir den mer i form av ett exempel, en skiss.
I det här fallet vet vi bara ett bestämt mått, nämligen att ökning av ärtlandets kortsida är 3m samt att denna ökning resulterar i att en rektangel blir en kvadrat. Så långt skissar vi bilden. Hur stort jordgubbslandet är har vi ingen aning om, förutom att det från början måste varit minst 15 m2. Efter ändringen skulle jordgubbslandet i teorin kunna vara allt från 0 till oändligt stort (men givet jordytans fysiska begränsningar kan det inte vara oändligt stort).
Nu till frågan om man bör rita så här till barnen.
När elever nått så långt i sin matematiska utveckling att de kan ta sig an ett sånt här problem bör de vara på det klara med att man kan rita bilder på det här skissartade sättet. Problemet kan givetvis presenteras utan bilden och blir då ännu lite svårare. Jag tycker att den svårigheten som tas bort genom att bilden visas egentligen är den viktigaste att träna på. Om jag som mellanstadielärare skulle undervisat med detta problem skulle jag givit problemet utan bild och sedan tillsammans med eleverna börjat med att bena ut vad vi får reda på och gemensamt ritat en figur. Just modelleringen av problemet är ofta det svåra och något viktigt att träna på och undervisa om.
Ett annat skäl till att man i problemlösning inte ritar en skalenlig bild i en problemformulering är att det då blir möjligt att lösa problemet med hjälp av mätning. För unga elever kan det vara en strategi, men de tränar då något helt annat. I det här fallet är ju knuten just att man inte från början vet hur stort ärtlandet är eller hur lång sidan i kvadraten är men att man ändå kan räkna ut det med hjälp av den informationen som ges. Bilden hjälper oss att se det om man kan se att bilden är en skiss, eller ”bara som ett exempel”. En viktig insikt.
Cecilia Kilhamn