Rationella tal. R

Innehåll

Add a header to begin generating the table of contents

Rationella tal. R

Diagnoserna i området avser att kartlägga elevernas förståelse och färdighet avseende tal i bråkform, tal i decimalform, proportionalitet och procent.

Bråk

Tal i decimalform

Proportionalitet och procent

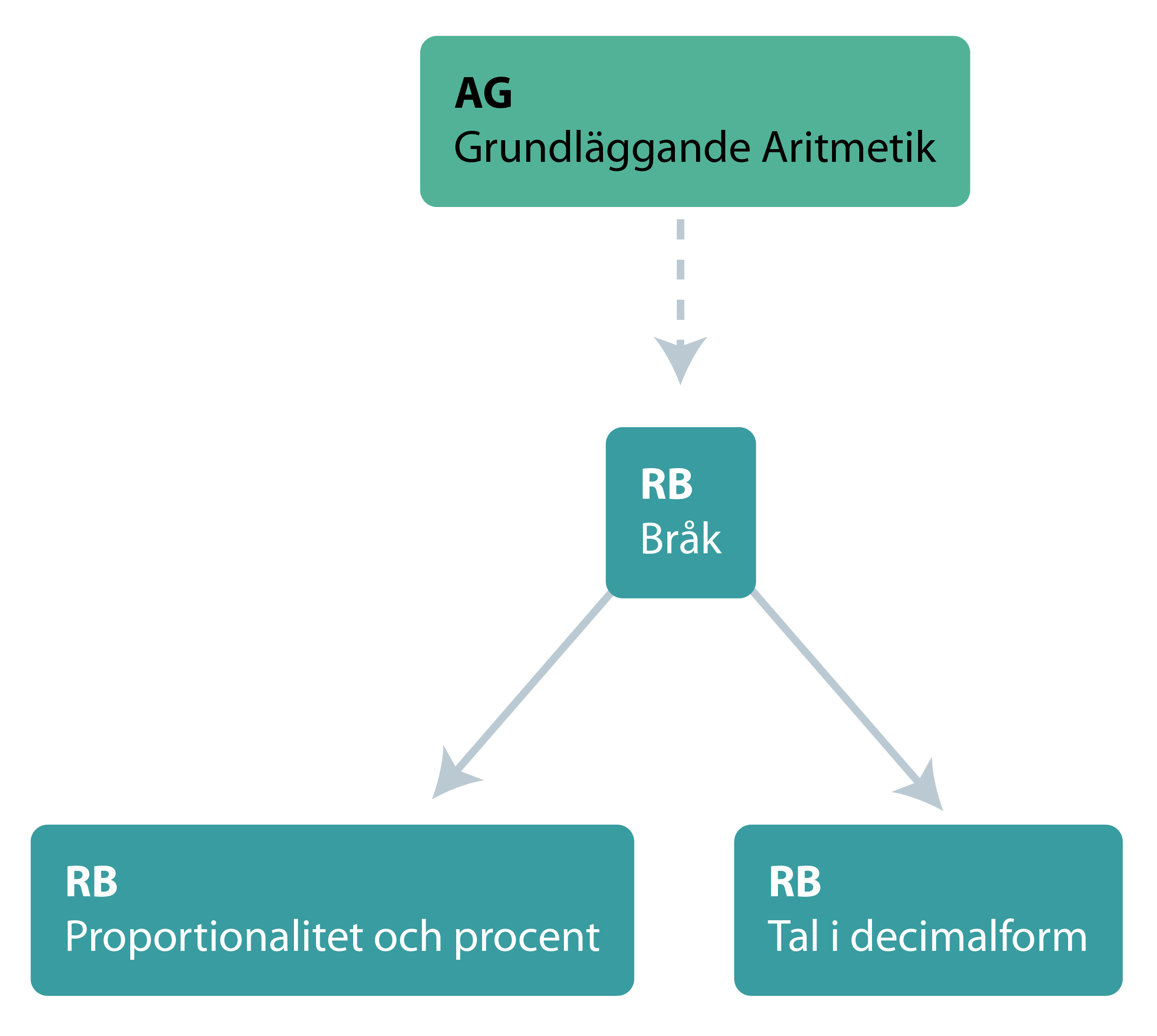
Sambanden mellan delområdena ser ut så här:

Strukturschemat visar att den grundläggande aritmetiken, AG omfattar förkunskaper till området och att delar av RB, tal i bråkform, utgör förkunskaper till proportionalitet och procent, RP och tal i decimalform, RD. Detaljer för detta framgår av strukturschemat för respektive delområde.

Området Rationella tal i relation till syfte och centralt innehåll i kursplanen i matematik

Område R omfattar delområdena RB, tal i bråkform, RD, tal i decimal form och RP, proportionalitet och procent, och handlar om de rationella talen och dess aritmetik. Logiskt sett borde givetvis RB, RD och RP vara delområden till A, aritmetik, men området A skulle då bli ohanterligt stort. Vi har därför valt att låta de rationella talen utgöra ett eget område.

Med hjälp av diagnoserna inom detta område kan man ta reda på kvalitet och omfattning av de begrepp och metoder som eleven har inom rationella tal för att kunna utveckla förmågan att:

formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder,
använda och analysera matematiska begrepp och samband mellan begrepp,
välja och använda lämpliga matematiska metoder för att göra beräkningar och lösa rutinuppgifter
föra och följa matematiska resonemang, och
använda matematikens uttrycksformer för att samtala om, argumentera och redogöra för frågeställningar, beräkningar och slutsatser

Beräkningar med rationella tal bygger på samma räknelagar och räkneregler som den övriga aritmetiken. Men nu är det en annan typ av tal jämfört med de naturliga talen som eleverna arbetat med tidigare. Genom att synliggöra detta i undervisningen underlättar man för eleverna att utveckla förmågan att kunna resonera, bygga begrepp och se samband samt att senare kunna generalisera den grundläggande aritmetiken till andra områden. Genom att tala matematik och göra skriftliga redovisningar ska eleven få hjälp att använda matematiska uttrycksformer och beräkningsmetoder inom området, på ett korrekt sätt.

Diagnoserna ger eleven möjlighet att visa kunskap inom följande centrala innehåll:

Det centrala innehållet som behandlar rationella tal finner man under rubrikerna Taluppfattning och tals användning och under Samband och förändring.

Årskurs 1–3

Taluppfattning och tals användning:

Del av helhet och del av antal. Hur delarna kan benämnas och uttryckas som enkla bråk samt hur enkla bråk förhåller sig till naturliga tal.
enkla tal i bråkform och deras användning i vardagliga situationer.

Samband och förändring:

Olika proportionella samband, däribland dubbelt och hälften

I kunskapskrav för godtagbara kunskaper i årskurs 3 finns följande:

Eleven visar grundläggande kunskaper om tal i bråkform genom att dela helheter i olika antal delar samt jämföra och namnge delarna som enkla bråk.
Eleven kan även använda och ge exempel på enkla proportionella samband i elevnära situationer.

Eleven ska alltså själv aktivt kunna dela helheter i olika antal lika stora delar och sedan uttrycka delarnas storlek med tal i bråkform. Detta förutsätter att eleven har förstått nämnarens och täljarens innebörd.

Årskurs 4–6

Taluppfattning och tals användning:

Rationella tal och deras egenskaper
Positionssystemet för tal i decimalform.
Tal i bråk- och decimalform och deras användning i vardagliga situationer.
Centrala metoder för beräkningar med… enkla tal i decimalform vid överslagsräkning, huvudräkning samt vid beräkningar med skriftliga metoder …

Samband och förändring:

Proportionalitet och procent samt deras samband
Grafer för att uttrycka olika typer av proportionella samband vid enkla undersökningar.

I kunskapskraven i slutet av årskurs 6 finns ingen direkt beskrivning i relation till det centrala innehållet men det är nödvändigt att eleverna behärskar grundläggande bråkräkning och räkning med tal i decimalform, inte minst med tanke på att bråkräkning är en viktig förkunskap såväl till räkning med procent som inom algebra.

Årskurs 7–9

Taluppfattning och tals användning:

Reella tal och deras egenskaper och användning i vardagliga och matematiska situationer.

Talsystemets utveckling från naturliga tal till reella tal:

Centrala metoder för beräkningar med tal i bråk- och decimalform vid överslagsräkning, huvudräkning samt vid beräkningar med skriftliga metoder…

Samband och förändring: R

Procent för att uttrycka förändring och förändringsfaktorer samt beräkningar med procent i vardagliga situationer och situationer inom olika ämnesområden

I kunskapskraven i slutet av årskurs 9, finns ingen direkt beskrivning i relation till det centrala innehållet, men arbete med rationella tal genomsyrar under dessa årskurser stora delar av skolans matematikundervisning.

Didaktiska kommentarer till område R

Bråkens roll i samhället har successivt övertagits av decimaltalen (bland annat efter införandet av SI-enheter för olika storheter). Detta får emellertid inte tolkas så att vi inte längre behöver undervisa om bråk i skolan. Bråket har fortfarande en stor roll att spela när det gäller att beskriva andelar och är samtidigt

en förkunskap för att lära sig algebra. Att elever kan multiplicera, dividera eller förlänga tal i bråkform är nödvändigt på flera av gymnasieskolans program.

Räkning med bråk är en förkunskap för såväl räkning med decimaltal som för algebra. Decimaltal är en speciell typ av bråk och reglerna för hur man multiplicerar och dividerar decimaltal är desamma som för tal i bråkform. Decimaltal är inte något annat än bråktal med nämnaren 10, 100, 1 000 etc. skrivna på ett annat sätt.

I vardagen använder man relativt sällan tal i bråkform. Gör man det är det snarare som namn på en storhet.

Du spelar en halvton för högt.

Hon kommer om en kvart.

I andra fall räcker det med att kunna tolka storleken av de nämnda ”bråken”.

Lektionen varade i tre kvart.

Bråkformen i de här exemplen är egentligen skenbar. En kvart är inte ett bråktal i egentlig mening utan utgör snarare en proportion.

När man studerar hur bråk behandlas i vardagen, och hur detta speglas i läromedel och under lektioner, visar det sig att bråk förekommer i en rad olika situationer. Det är emellertid inte lätt att genomskåda på vilket sätt de matematiska modellerna för bråkräkning används i dessa olika situationer. Man kan uttrycka detta som att bråken har många ansikten/aspekter. Ett bråk kan uppfattas på bland annat följande sätt, som:

ett tal,
en del av en hel,
en del av ett antal,
en andel,
en proportion,
ett förhållande t.ex. en skala.
division som metafor.

För att lösa problem som hör samman med de olika situationerna använder man sig av bråken som rationella tal och opererar med dem enligt gällande räknelagar. Det är emellertid inte alltid lätt för en elev att se sambanden mellan de olika situationerna. För en elev är det inte så lätt att inse att man kan arbeta med \(\frac{2}{3}\) av en helhet och \(\frac{2}{3}\) av ett antal utgående från samma matematiska modell, eller att en strategi som beskrivits för del av en hel också gäller för en del av ett antal. När man själv behärskar detta och därmed tar det för givet, kan det vara svårt att föreställa sig elevernas problem.

Eftersom de räkneregler som gäller för tal i decimalform bygger på motsvarande regler för tal i bråkform är det lämpligt att behandla tal i bråkform före tal i decimalform, så att reglerna för hur man opererar med decimaltal inte enbart blir procedurella utan att eleverna får förståelse.

Varje reellt tal kan utvecklas i decimalform med en decimalutveckling som är

ändlig om talet är ett decimaltal, \(\frac{3}{8}\) = 0,375
oändlig och periodisk om talet är ett rationellt tal, som inte är ett decimaltal, \(\frac{2}{3}\) = 0,666 66… eller \(\frac{16}{37}\) = 0, 432 432 4…
oändliga och ickeperiodiska om talet är ett irrationellt tal, π = 3, 141 59…

Varje bråk kan skrivas som en ändlig eller periodisk decimalutveckling. I vissa fall består perioden av enbart nollor. Sådana tal kallas för decimaltal.

Alla rationella tal (tal i bråkform) kan uttryckas i decimalform och har en plats på tallinjen vilket gör att Positionssystemet för tal i decimalform utgör ett centralt undervisningsinnehåll. För att undvika en rad räknefel bör ett tal som 3,25 läsas 3 hela och 25 hundradelar och även kunna tecknas som \(3\frac{25}{100}\) eller ännu hellre \(3 + \frac{25}{100}\). Mellan två rationella tal på tallinjen

finns det alltid oändligt många andra rationella tal. Mellan talen 0,25 och 0,26 finns t.ex. talen 0,251, 0,252 … och 0,2511, 0,2512, … osv.

För att avgöra vilket av två tal i decimalform som är störst, t.ex. 3,547 och 3,539, börjar man med att jämföra entalen. De är lika stora. Därefter jämför man tiondelarna. De är lika stora. I nästa steg jämför man hundradelarna. Eftersom 4 hundradelar är större än 3 hundradelar så är talet 3,547 störst, oberoende av tusendelen.

En förutsättning för att man skall kunna addera eller subtrahera två tal är att de är jämförbara. Man adderar t.ex. inte storheter som 2 cm och 3 mm utan att först uttrycka dem i samma enhet. Mätetalet blir alltså inte 2 + 3 = 5 utan 20 + 3 = 23 (mm) eller 2 + 0,3 = 2,3 (cm). På motsvarande sätt utför man inte subtraktioner som 2,10 – 2,9 utan att först skriva talen i samma enhet, nämligen hundradelar. Det bli då lätt att se att 2,10 är ett mindre tal än 2,90.

Finns det verkligen tal mellan 1 och 0,9? Att skriva talen i samma enhet, alltså som 1,0 och 0,9 hjälper inte heller. Det gäller att inse att varje tal i decimalform kan skrivas på olika sätt. I det här fallet kan talen också skrivas som 1,00 och 0,90 eller 1,000 och 0,900 (jämför förlängning och förkortning av bråk). En bra metafor för detta är tallinjen. De första tiondelarna på tallinjen ser ut så här, uttryckt i såväl bråkform som decimalform.

Av tallinjen framgår det tydligt att det är ett avstånd mellan 0,9 och 1,0. På den sträckan finns det nya tal. Om man nu förstorar tallinjen mellan 0,9 och 1,0 tio gånger så ser det ut så här. I det här fallet bör talen skrivas som 0,90 och 1,00 eftersom noggrannheten nu är en hundradel.

Det här betyder att det mellan talen 0,9 och 1 finns åtminstone nio tal, 0,91, 0,92, …, 0,99. Sträckan mellan 0,91 och 0,92 kan i sin tur förstoras upp tio gånger så mellan dessa tal ligger det åtminstone nio nya tal nämligen 0,911, 0,912, …, 0,919. Eftersom detta kan upprepas i all oändlighet visar det sig att det i själva verket finns oändligt många tal mellan decimaltalen 0,9 och 1,0.

Man kan också uttrycka detta på följande sätt. De naturliga talen känner sina grannar. Talen 8 och 10 är grannar till 9. Bland de naturliga talen finns inga tal mellan 9 och 10. När man kommer till de rationella talen (decimaltalen är rationella tal) så är det tvärtom. De rationella talen känner inte sina grannar. Det förhåller sig i stället så att det mellan två godtyckligt valda decimaltal finns oändligt många tal. Det är detta som demonstreras med hjälp av ovanstående tallinjer.

Inom de naturorienterande ämnena är det viktigt att man anger noggrannheten i en mätning. Om man anger att en sträcka är 1,9 meter lång, så menar man något helt annat än om man anger att sträckan är 1,90 meter lång. Detsamma gäller för matematikens avrundningsregler. När man anger en sträcka till 1,9 meter, så menar man i allmänhet att den är mellan 1,85 meter och 1,95 meter lång. Det betyder att decimaltalet 1,9 oftast tolkas som ett tal inom det skuggade området i figuren.

Det här betyder i sin tur att man inte kan avgöra vilket tal som är störst, 1,9 eller 1,86. Som framgår av nedanstående figur så kan 1,9 vara såväl större som mindre än 1,86. Däremot vet man med säkerhet att 1,90 är större än 1,86.

I en inledande undervisning kanske man ska undvika att jämföra tal som 1,86 och 1,9. Får man en sådan uppgift bör man direkt ställa följdfrågan vad avses. Menar man 1,90 eller 1,9? Om talen hade angetts i samma enhet eller skrivits om så att de fick samma enhet så hade uppgifterna varit enkla att lösa. Då hade en uppgift som att jämföra talen 3,521, 3,6 och 3,75 i stället handlat om att jämföra talen 3,521, 3,600 och 3,750 och det hade inte rått någon tvekan om vilket tal som var störst.

Dagligen möter man procentbegreppet i olika situationer. De matematiska modeller som används vid procenträkning har sina rötter i bråkräkningen och handlar i grunden om att räkna med andelar. Det krävs därför en god taluppfattning kopplad till bråk och decimaltal för att eleverna skall lyckas med procenträkning. Man bör därför ge eleverna möjlighet att få en fördjupad förståelse av procentbegreppet så att det fungerar vi problemlösning.

Rationella tal. Alla diagnoser

Bråk. RB

Delområdet RB omfattar följande sju diagnoser:

RB1

En del av en hel

RB2

Flera delar av en hel

RB3

Del av ett antal

RB4

Bråk som tal

RB5

Taluppfattning av bråk

RB6

Addition och subtraktion av tal i bråkform

RB7

Multiplikation och division av tal i bråkform

Diagnoserna inom delområdet bygger på att elever har en (intuitiv) kunskap om del av en helhet eller delar av ett antal samt att de behärskar de grundläggande räknelagarna från AG1.
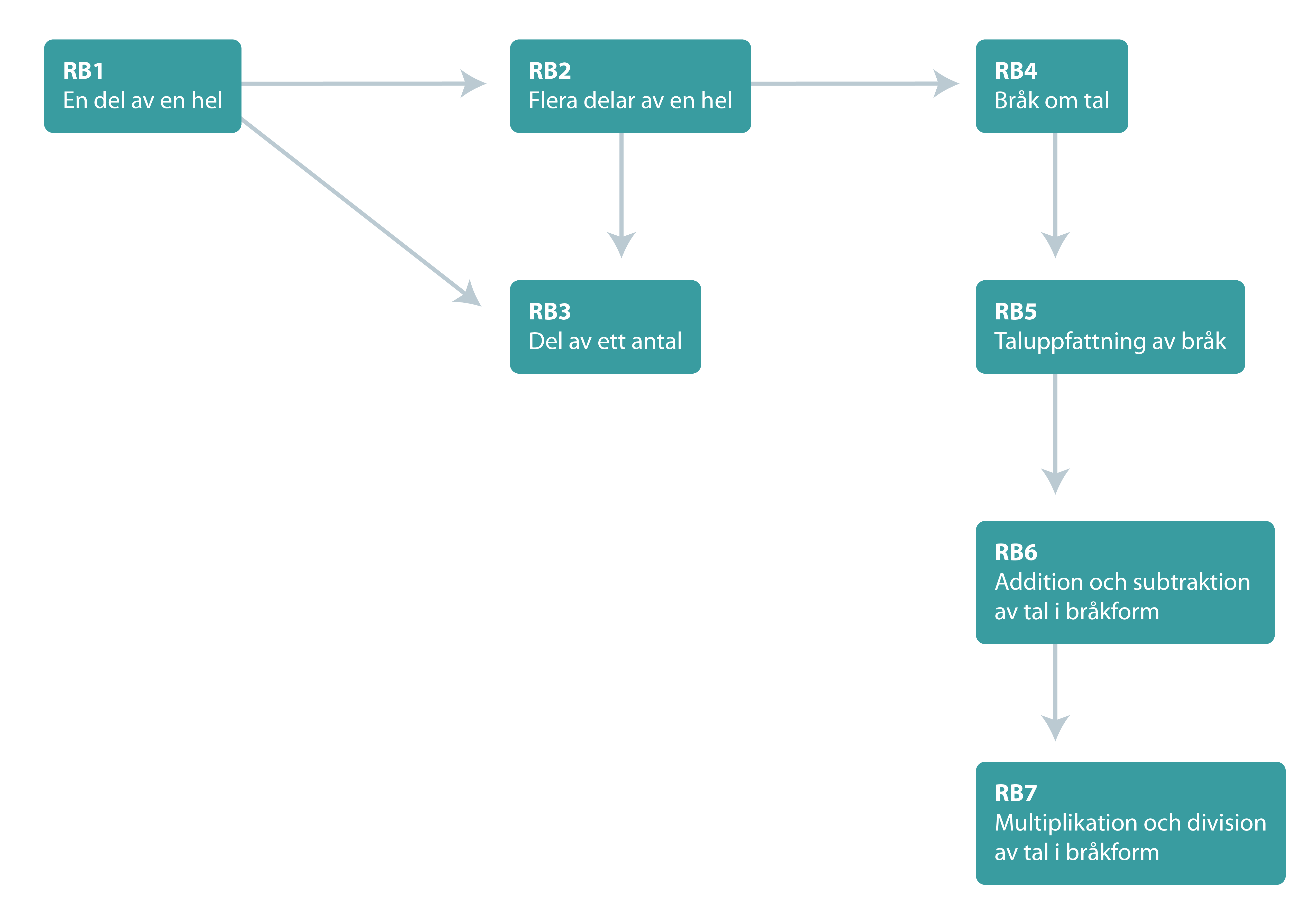
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan.

Där framgår att för att arbeta med bråk som tal RB4 –RB7 krävs konkretiserande förkunskaper från RB1–RB3. Lägg märke till att arbetet med tal i decimalform kräver förkunskaper från RB4.

Didaktiska kommentarer till delområdet RB

Räkning med bråk är en förkunskap såväl för räkning med tal i decimalform som för algebran.

Bråk används för att beskriva en rad olika fenomen inom vardagens matematik. De olika aspekterna kan beskrivas som bråkets olika ansikten.

Bråk som beskriver tal . Tal som \(\frac{3}{7} \) och \(\frac{2}{5} \)har liksom talen 2, 3 och 5 en plats på tallinjen. De kan också definieras med hjälp av divisionerna 3/7 och 2/5. Vissa av bråken såsom \(\frac{2}{5} \) kan också skrivas som ett avslutat decimaltal, i det här fallet som 0,4.
Däremot kan talet \(\frac{3}{7} \) inte skrivas som ett avslutat decimaltal, men kan ges ett hur noggrant närmevärde som helst med hjälp av en decimalutveckling såsom 0,428571428571…
Bråk som beskriver en eller flera andelar av en hel
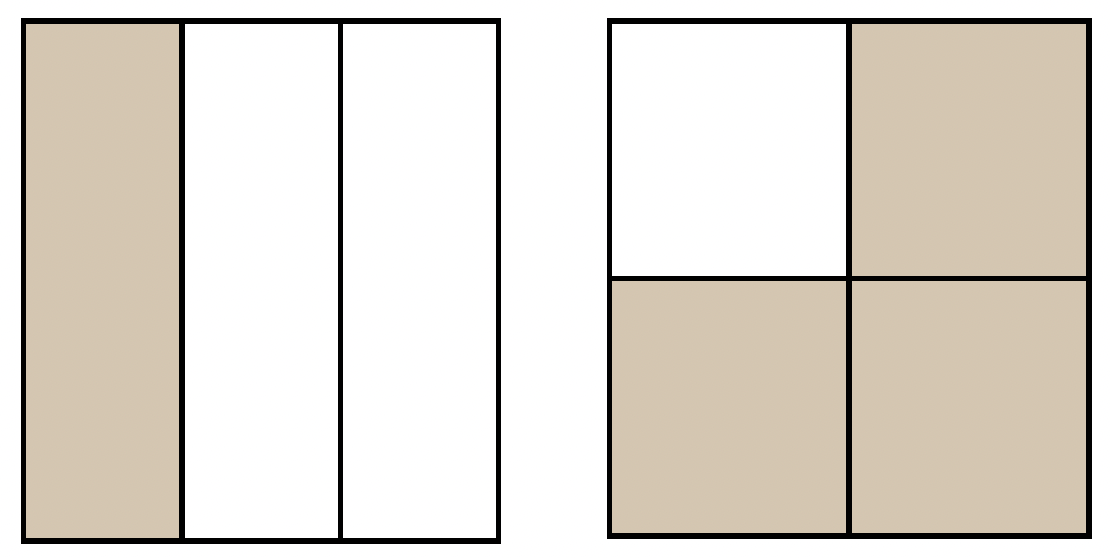
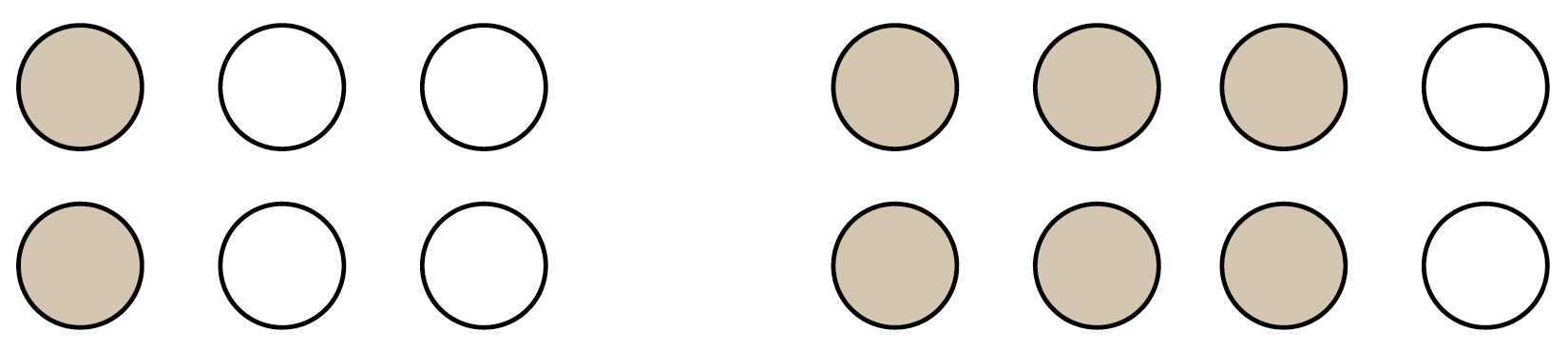
Talen 1/3 och 3/4 kan illustreras så här:

Bråk som beskriver en eller flera andelar av ett antal. En tredjedel av 6 och 3 fjärdedelar av 8 kan beskrivas så här:

Bråk som beskriver proportion. Ett exempel på detta är att 7 av 10 elever vill ha pizza på skollunchen. (Detta kan också beskrivas som att 70 % av dem vill ha pizza till lunch.)
Bråk som används för att beskriva skala. I dessa fall skrivs bråken ofta som 5:1 eller 1:20 000.
Bråk som används även för att ange förhållande. Om man ska dela ett 7 m långt rep i förhållandet 2:5, så blir andelarna 2/7 respektive 5/7.

Man kan konstatera att bråk används i en rad olika situationer. Många elever har redan vid skolstarten
en intuitiv uppfattning om bråk och andelar. Denna intuitiva vardagsuppfattning kan användas i undervisningen på ett sådant sätt att eleverna ges möjligheter att uppfatta begreppen och att på sikt formalisera dem. De flesta diagnoserna i området förutsätter att eleverna har en god taluppfattning och behärskar grundläggande aritmetik. För att förstå varför en division med ett bråk mindre än ett i nämnaren ger en kvot större än täljaren måste division förstås som innehållsdivision. Till exempel bör en uppgift som: \(\frac{4}{(\frac{1}{3})} = 12\) lösas genom tanken att det ryms 12 stycken tredjedelar i 4 hela.

Tal i decimalform. RD

Delområdet RD omfattar följande sex diagnoser:

RD1

Tal i decimalform

RD2

Taluppfattning av decimaltal, addition och subtraktion

RD3

Taluppfattning av decimaltal, multiplikation och division

RD4

Addition och subtraktion av tal i decimalform

RD5

Multiplikation och division av tal i decimalform

RD6

Avrundning och gällande siffror

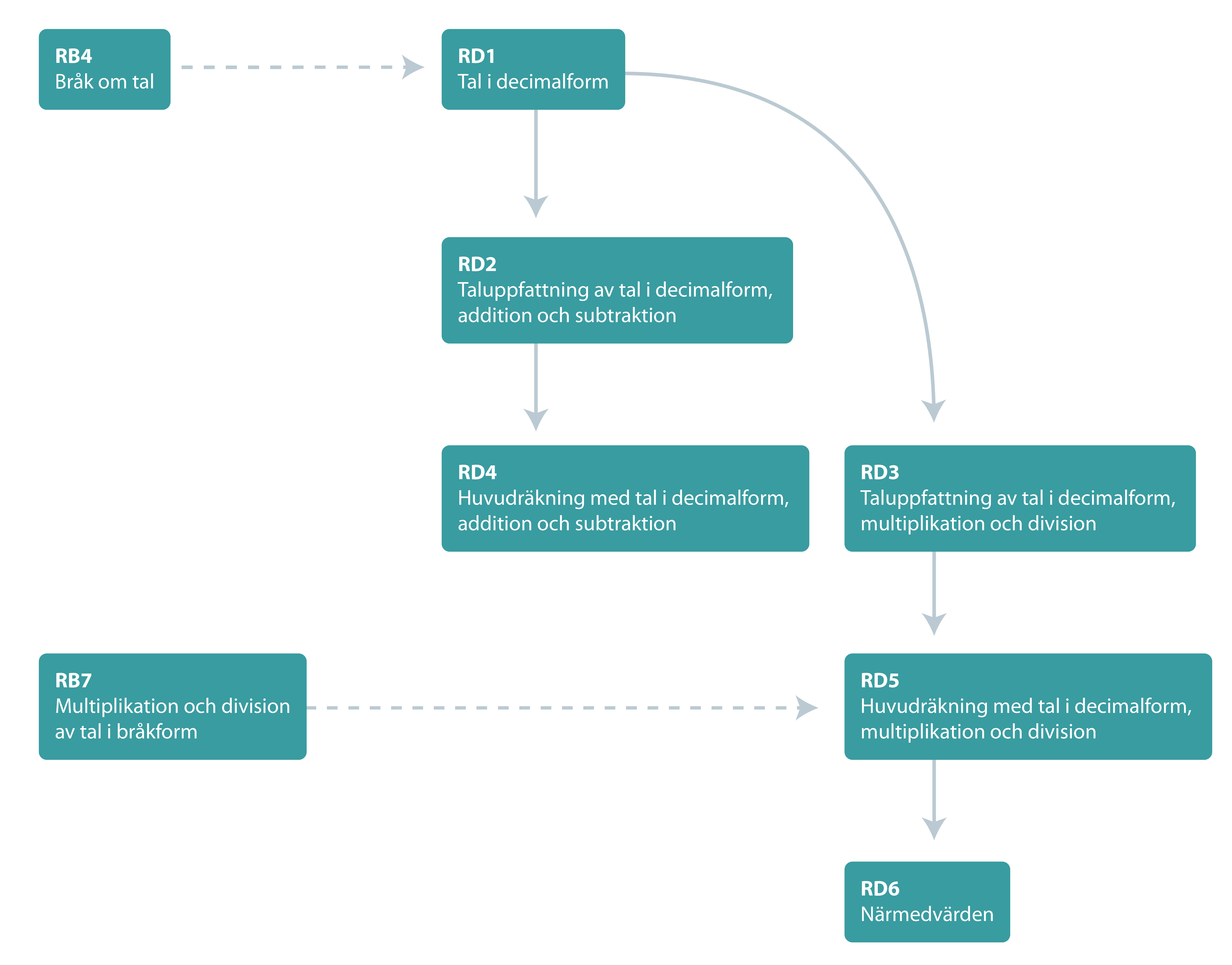
Eftersom decimalformen är ett speciellt sätt att uttrycka bråk med nämnare som 10, 100 osv. krävs förkunskaper från RB4. För att operera med tal i decimalform kräv dessutom förkunskaper från område A. Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Där framgår att taluppfattning av tal i decimalform föregår operationer med dessa tal. Här gäller det huvudräkning i RD2 och RD3 men dessa diagnoser utgör i sin tur förkunskaper till AS9, AS10 och AS11 som testar skriftlig räkning med tal i decimalform.

Didaktiska kommentarer till delområdet RD

Diagnoserna inom detta delområde innehåller uppgifter som eleven ska lösa med hjälp av effektiva huvudräkningsstrategier vilket förutsätter att eleven har god taluppfattning när det gäller tal i decimalform. Skriftlig räkning med tal i decimalform prövas inom diagnoser i Aritmetik, delområdet skriftlig räkning (AS). Decimaltal kan ses som tal i bråkform där man uttryckt bråket med hjälp av nämnaren 10, 100, 1 000 och så vidare. I undervisningen behöver du ägna tid åt att diskutera decimaltalens egenskaper och uppbyggnad och det är viktigt att eleverna ges möjlighet att utveckla språklig förståelse och innebörd av positionernas värde. Detta för att räkningen med decimaltal inte ska bli alltför procedurell. På samma sätt som man diskuterar ental, tiotal, hundratal och tusental när det gäller de naturliga talen bör man hantera tiondel, hundradel, tusendel och så vidare när det gäller decimaltalen.

375 ska förstås som:

Hundratal	Tiotal	Ental
3	7	5

3,75 ska förstås som:

Ental	Tiondel	Hundradel
3	7	5

Till exempel behöver eleverna förstå talet 2,75 som 2 + 7/10 + 5/100 det vill säga som 2 hela, 7 tiondelar och 5 hundradelar. Detta för att kunna jämföra med talet 2,8 som då betyder 2 + 8/10 (+ 0/100) det vill säga 2 hela och 8 tiondelar (och inga hundradelar, det samma som 2,80) och på så sätt förstå varför 2,8 (“två komma 8”) är större än 2,75 (“två komma 75”), trots att 75 är mer än 8. De båda talen kan jämföras enligt:

Ental	Tiondel	Hundradel
2	7	5

Ental	Tiondel	Hundradel
2	8	0

Effektiva räknestrategier för tal i decimalform bygger liksom räkning med naturliga tal på god förståelse för räknesättens innebörd. Till exempel att subtraktion kan ses som skillnad och att en uppgift som 7,2 – 3,9 därför kan beräknas som 7,3 – 4,0 (ett lika-tillägg med 0,1 på båda termer) = 3,3. Samt att 1,2/0,6 = 2 eftersom 0,6 ryms två gånger i 1,2 (innehållsdivision).

Proportionalitet och procent. RP

Delområdet RP omfattar följande sju diagnoser:

RP1

Grundläggande proportionalitet

RP2

Proportionalitet i grafform

RP3

Grundläggande procent

RP4

Procenträkning

RP5

Procent, problemlösning

RP6

Förändringsfaktor

RP7

Ränta

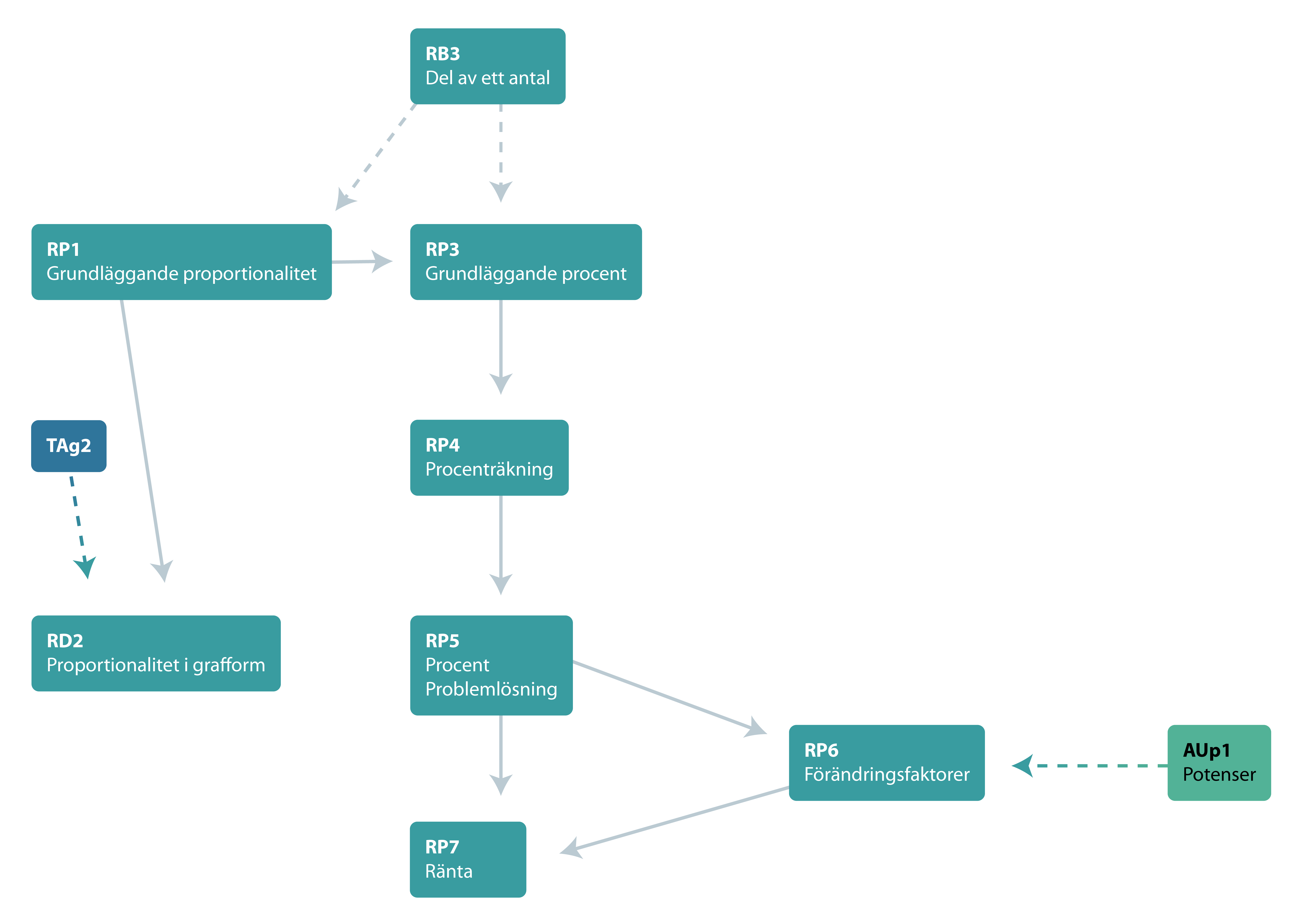
Arbete med proportionalitet har sin grund i bråk och bråkräkning och bygger tekniskt sett på arbete med tal i decimalform. Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Där framgår det att, RB3, del av ett antal, utgör förkunskap till delområdet. Vidare syns att RP2 kräver förkunskaper från TAg2, koordinatsystem och rätalinjen. För arbete med förändringsfaktor RP6 behövs förkunskaper från AUp1 potenser.

Didaktiska kommentarer till delområdet RP

Procenträkning har sin grund i bråkräkning och handlar om att räkna med andelar. För att på djupet förstå procenträkning behöver eleverna ha en god taluppfattning inom tal i bråkform och tal i decimalform. Ordet procent har sitt ursprung i latinets per centum, vilket kan översättas till för varje hundrade. När man undervisar om procent bör man skilja mellan att behärska enkla procedurer som kan utföras med hjälp av en miniräknare och att ha en djupare förståelse av procentbegreppet.

För eleverna är det inte alltid så lätt att förstå kopplingen mellan decimalform och procentform. Procent utgör alltid en andel av något och kan aldrig vara ett uttryck för ett enskilt tal.

Till exempel betyder 20 % av 70 andelen \(\frac{20}{100}\) av 70 som i sin tur betyder \( 20\cdot (\frac{1}{100} \hbox{ av } 70)\), alltså 20 · 0,7 = 14.

Detta motsvaras av den i dag vanliga metoden att först räkna ut hur mycket 1 % är för att sedan, i detta fall, multiplicera det med 20 för att få fram hur mycket 20 % av 70 är.

Detta betyder att det är olämpligt att skriva 0,20 = 20 % eftersom 0,20 är ett tal och 20 % är en andel. Visserligen är 20 % av 1 = 0,20, men 20 % av 10 är ju lika med 2.

Beräkningen 20 % av 70 = 0,20 · 70 = 14 ger samma svar, men det kan bli problematiskt att förstå 20 % som 0,20 eftersom 20 % i så fall måste betraktas som ett namn på talet 0,2. Men på svenska blir detta väldigt konstigt. Vi kan ju inte säga att 0,2 av de röstande tyckte att skolmaten var god om vi menar att 20 % av de röstande tyckte att skolmaten var god.

0,2 och 20 % är alltså inte synonyma på svenska. Detta beror just på att 0,2 betecknar ett tal medan 20 % betecknar en andel, i det här fallet andelen röstande. Skriver vi 1/5 av de röstande tyckte att skolmaten var god, betecknar 1/5 också en andel och inte ett tal. Problemet här är att bråkstrecket är flertydigt; 1/5 kan i vissa sammanhang beteckna en andel, som när vi talar om andelen röstande, men i andra ett tal, som i 1/5 > 1/6 eller 1/5 · 1/6.

I uttrycken 20 % = 1/5 = 0,2 gör vi alltså felet att vi blandar ihop de två olika betydelserna hos bråkstrecket. I den första likheten läser vi 1/5 som 1 andel av 5. I den andra läser vi 1/5 som ett namn på talet 1/5 eller 0,2. Sedan använder vi i den första läsningen dessutom likhetstecknet på ett felaktigt sätt i och med att vi i den första läsningen inte använder vare sig 20 % eller 1/5 som termer. Det är således olämpligt att skriva ett uttryck som det ovan. Skriv 20 % av X = 1/5 av X som uttrycker andelar och 1/5 = 0,2 som är tal.

Om man vill ange hur många procent 12 elever utgör av 30 elever är det hur stor andel dessa 12 elever utgör av hela gruppen (30 stycken) man vill veta. Andelen är 12 av 30, vilket i bråkform uttrycks som andelen \(\frac{12}{30} \). Detta kan i sin tur uttryckas som \(\frac{4}{10} \) vilket kan uttryckas som \(\frac{40}{100} \) och denna andel kan uttryckas som 40 %.

Använder man division som metafor vet man att andelen \(\frac{12}{30} \) vid division ger kvoten 0,4= 0,40 (det vill säga 40 hundradelar) = 40 %.

Rationella tal. R

Rationella tal. R

Rationella tal. R

Området Rationella tal i relation till syfte och centralt innehåll i kursplanen i matematik

Årskurs 1–3

Årskurs 4–6

Årskurs 7–9

Didaktiska kommentarer till område R

Rationella tal. Alla diagnoser

Bråk. RB

Didaktiska kommentarer till delområdet RB

Tal i decimalform. RD

Didaktiska kommentarer till delområdet RD

Proportionalitet och procent. RP

Didaktiska kommentarer till delområdet RP

Börja skriva och tryck enter för att söka