Mätning. M
Mätning. M
Mätning. M
Diagnoserna i området avser att kartlägga elevernas kunskaper i att mäta och uppskatta längd, area, volym, tid och massa och om de kan göra de vanligaste enhetsbytena.
Området består av följande sex delområden:
MGF
Förberedande mätning och geometri som finns på område Mätning
MTi
Mätning av tid
MMa
Mätning av massa
MLä
Mätning av längd
MAr
Mätning av area
MVo
Mätning av volym
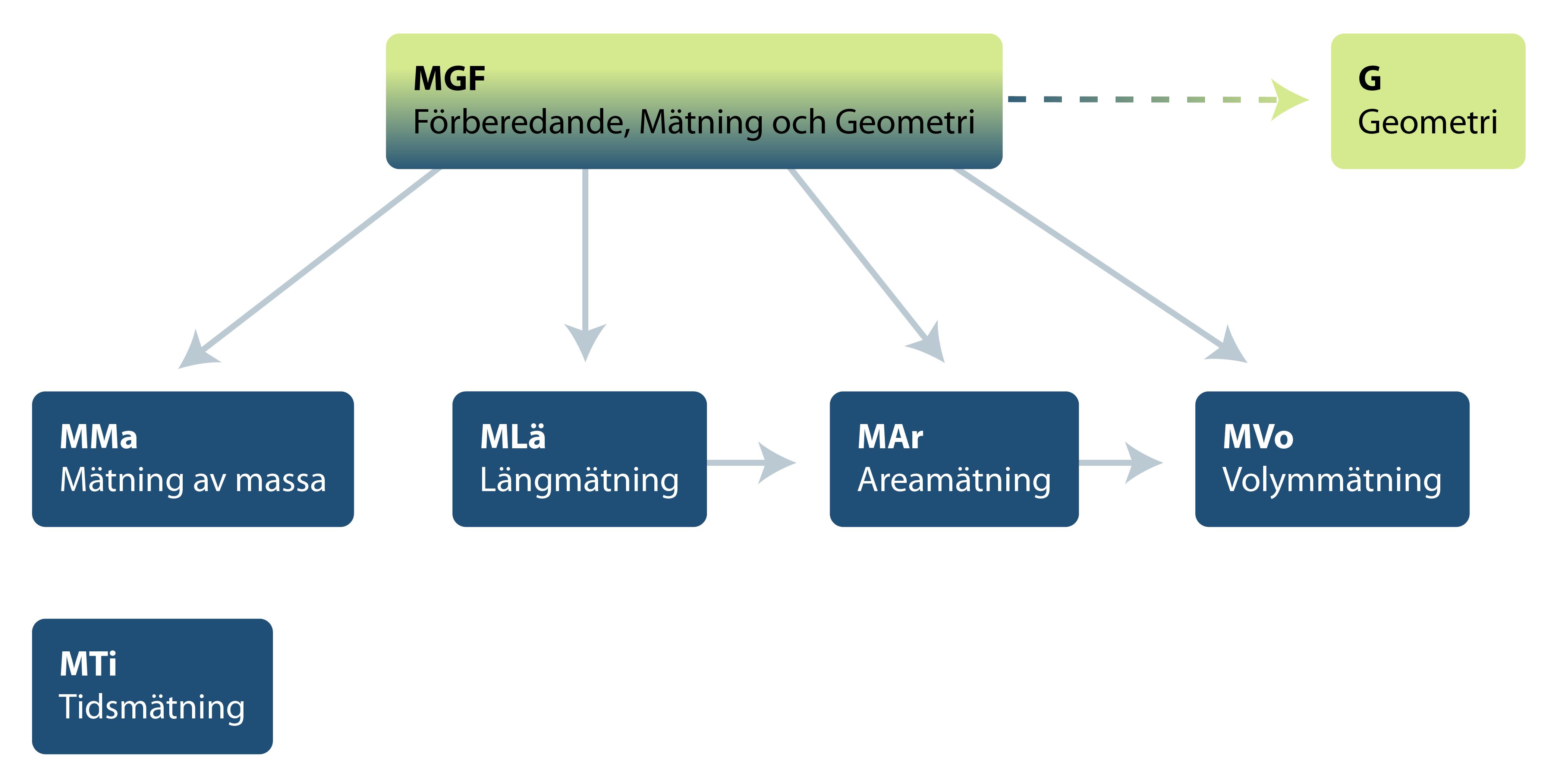
Sambanden mellan delområdena ser ut så här:
I kursplanen nämns även mätning av vinklar. Diagnoser om vinkelmätning finns i området Geometri under delområdet vinklar (GVi).
Strukturschemat visar att diagnosen Förberedande mätning och geometri (MGF) innehåller förkunskaper både till Mätning och Geometri. Strukturschemat visar också att längdmätning (MLä) är förkunskap till areamätning (MAr) som i sin tur är förkunskap till mätning av volym (MVo), i de fall volym mäts med kubikenheter. Volym kan även mätas med grundenheten liter och kräver då inte dessa förkunskaper.
Området Mätning i relation till syfte och centralt innehåll i kursplanen i matematik
Med hjälp av diagnoserna inom detta område kan man ta reda på kvalitet och omfattning av de begrepp och metoder som eleven har inom mätning för att kunna utveckla förmågan att:
- formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder,
- använda och analysera matematiska begrepp och samband mellan begrepp,
- välja och använda lämpliga matematiska metoder för att göra beräkningar och lösa rutinuppgifter,
- föra och följa matematiska resonemang, och
- använda matematikens uttrycksformer för att samtala om, argumentera och redogöra för frågeställningar, beräkningar och slutsatser.
Området mätning är rikt på begrepp, det börjar redan med jämförelseorden som testas i fördiagnosen MGF. Det är också avgörande att eleverna förstått mätandets idé för att ha möjlighet att förstå vad mätning av en storhet går ut på. Val av lämplig metod för mätning samt val av lämplig enhet, rimlig noggrannhet och personligt valda referenser för att kunna göra uppskattningar är också viktiga förmågor som eleven bör få möjlighet att utveckla genom arbetet med mätning.
För att kunna diskutera mätning, krävs det att man behärskar termerna för de begrepp som används. En sträcka har t.ex. en längd och en yta (ett område) har en area. Ett annat exempel är att basytan till en tetraeder har sidor, samtidigt som dessa sidor är kanter i tetraedern. Basytan är i sin tur en sida (sidoyta) till tetraedern.
Diagnoserna ger eleven möjlighet att visa kunskaper inom följande centrala innehåll:
Det centrala innehållet som behandlar mätning finner man under rubriken Geometri. Vi har valt att ha Mätning som ett eget område eftersom det är omfattande och många diagnoser främst riktar sig till de tidigare årskurserna.
Årskurs 1–3
Geometri:
- Grundläggande geometriska objekt.
- Vanliga lägesord för att beskriva föremåls och objekts läge i rummet.
- Jämförelser och uppskattningar av matematiska storheter. Mätning av längd, massa, volym och tid med vanliga nutida måttenheter.
I kunskapskrav för godtagbara kunskaper i årskurs
3 finns följande: – Eleven kan göra enkla mätningar, jämförelser och uppskattningar av längder, massor, volymer och tider och använder vanliga måttenheter för att uttrycka resultatet. Eleven ska alltså själv aktivt kunna utföra mätningar av dessa storheter och sedan uttrycka resultatet med lämplig enhet. Detta förutsätter att eleven har förstått mätandes idé.
Årskurs 4–6
Geometri:
- Metoder för hur omkrets och area hos olika tvådimensionella geometriska figurer kan bestämmas och uppskattas.
- Jämförelse, uppskattning och mätning av längd, area, volym, massa och tid med vanliga måttenheter. Mätningar med användning av nutida och äldre metoder.
I kunskapskraven i slutet av årskurs 6 finns ingen direkt beskrivning i relation till det centrala innehållet men det är nödvändigt att förstå begrepp som t.ex. omkrets och area och kunna mäta olika storheter samt i samband med det göra olika beräkningar för att kunna visa olika grad av förmågor. Av kunskapskraven framgår att eleven ska utveckla sin förmåga att välja och använda ändamålsenliga och effektiva matematiska metoder med god anpassning till sammanhanget för att göra enkla beräkningar och lösa enkla rutinuppgifter inom bland annat geometri och mätning med allt bättre resultat.
Årskurs 7–9
Geometri:
- Metoder för beräkning av area, omkrets och volym hos geometriska objekt, samt enhetsbyte i samband med detta.
I kunskapskraven i slutet av årskurs 9, finns ingen direkt beskrivning i relation till det centrala innehållet, men det är nödvändigt att förstå begrepp och formler som till exempel volym och begränsningsarea och i samband med detta kunna utföra beräkningar för att visa olika grad av förmåg
Didaktiska kommentarer till område M
Barn utvecklar en rumsuppfattning redan under sina första levnadsår. De ord och begrepp de då använder överensstämmer inte alltid med de matematiska begrepp som lärare utgår från i skolans arbete. Eleverna behöver därför på ett tidigt stadium hjälp med att bygga upp en god uppfattning om grundläggande begrepp och ett motsvarande språk för att kommunicera dessa begrepp.
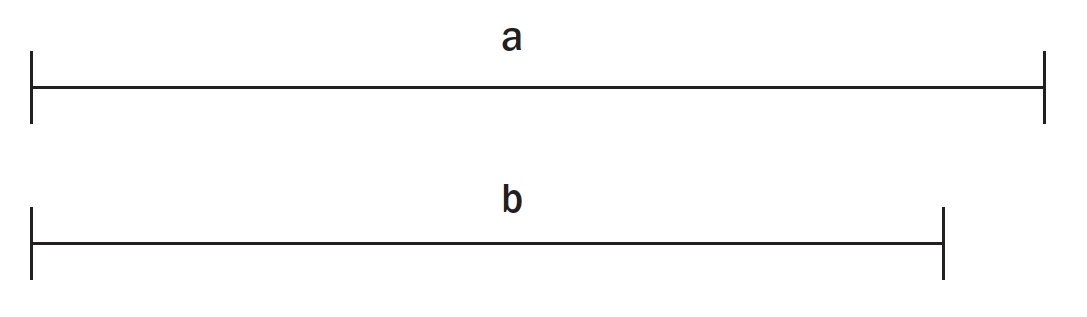
All mätning handlar i grunden om jämförelse. Som exempel kan vi ta mätning av sträckor. Man kan då använda sig av direkt eller indirekt jämförelse.
Vid direkt jämförelse av två sträckor a och b lägger man sträckorna (föremålen) bredvid varandra. Man finner då direkt att a > b.
Om a och b inte kan läggas intill varandra använder man sig istället av en indirekt jämförelse. För att jämföra sträckorna a och b kan man då använda en tredje sträcka c som referens. Om c är längre än a och b kan man avsätta längden av a på c och därefter jämföra den sträckan med längden av b. Referensen c kan antingen vara ett standardiserat mått eller ett ostandardiserat mått såsom ett kroppsmått. Man kan också välja en enhetssträcka c som är kortare än a och b, och se hur många enhetssträckor c som behövs för att mäta a respektive b.
Liknande teknik kan användas om man vill jämföra längden av tre sträckor: a, b och c. Man kan då börja med att jämföra a och b. Om a är längst kan man fortsätta med att jämföra b och c. Om då b är längst så vet man att a > b > c. Om istället c är längre än b fortsätter man med att jäma föra a och c. Den lag som då används kallas för den transitiva lagen: a ≥ b ≥ c. Mätning av area, volym obch tid följer i stort samma principer.
Resultaten av en mätning redovisas oftast som en storhet, t.ex. 5 kg. Storheten består i sin tur av två delar: mätetalet 5 och enheten kg. Beroende på storleken av det som mäts, gäller det att välja en lämplig enhet. Det är därför praktiskt att känna till relationerna mellan olika enheter och kunna göra enhetsbyten. Det är också praktiskt att känna till de vanligaste s.k. prefixen som följer ett mönster som bygger på det tiobassystem som vår talrad grundar sig på: kilo betyder 1 000, hekto 100, deci 0,1, centi 0,01 och milli 0,001. Att utföra enhetsbyten kräver ofta en god taluppfattning, inte minst när enhetsbytena omfattar mätetal uttryckta i decimalform.
Mätandet har historiskt sett börjat med lokala mått. För längdmätning har det ofta varit fråga om kroppsmått som fot eller tum. Efter hand som handel och sjöfart utvecklades blev det viktigt att dessa lokala mått standardiserades. Så småningom utvecklades de internationella mått som går under beteckningen SI-enheter. I de här diagnoserna används SI-enheterna för längd (meter), massa (kilogram) och tid (sekund) och därifrån härledda enheter.
Mätning används i en rad vardags- och yrkessituationer, men mätning av längd, area, volym och vinklar är också viktiga förkunskaper till geometrin. (En diagnos som omfattar mätning av vinklar finns i diagnosområdet Geometri). Vid vardagens mätning av volym används litermåttet som enhet och en liter kan i sin tur indelas i dl, cl och ml. 100 liter kallas 1 hektoliter. Det förekommer även äldre mått vid matlagning såsom kkp (kaffekopp), msk (matsked) och tsk (tesked). Inom geometrin används istället enheten 1 m3, som i sin tur kan delas in i 1 000 dm3. 1dm3 kan i sin tur delas in i 1 000 cm3 eller 1 000 000 mm3. Här motsvaras 1 dm3 av 1 liter och 1 cm3 av 1 milliliter.
Genom bl.a. Piagets forskning känner vi till betydelsen av att barn kan konservera (bevara i minnet) area och volym. Barn som inte kan detta tror att en ytas area eller en vätskas volym påverkas av dess form och får därmed problem med att förstå mätandets principer. På motsvarande sätt kan termerna för jämförelse och för att beskriva kroppars läge i rummet vara besvärliga. Detta påverkar givetvis barnets förmåga att kommunicera vissa begrepp.
De här diagnoserna omfattar inte mätandet med informella enheter, utan mäter om eleverna behärskar vanliga formella enheter för att uppskatta, mäta och ange storlek. Att mäta med informella enheter kan vara en metodisk väg att nå målen, och denna väg kan se olika ut.
Med undantag av diagnos Förberedande mätning och geometri (MGF) är diagnoserna skriftliga och visar därför inte om eleverna kan utföra dessa mätningar och uppskattningar i praktiska situationer. Lärare kan själva komplettera diagnoserna genom att låta eleverna mäta massa, volym och tid som en del av undervisningen.
De flesta varor vi köper i en butik är redan uppmätta och om det krävs en vägning så sker det med digitala vågar där mätandets idé inte blir synlig. Det betyder att många av dagens elever har begränsade erfarenheter av att mäta massa och volym. Detsamma gäller digital tid. På en analog urtavla ges en geometrisk bild av tiden ungefär som på ett cirkeldiagram. Detta gör det enklare att uppfatta dygnets delar och tidsdifferenser. Det digitala uret ger bara information om en aktuell tidpunkt och ställer därmed helt andra krav på beräkning av tidsdifferenser.
För alla storheter gäller att det är viktigt att eleverna får upplevelser och erfarenheter av olika mått. Utan referenser till upplevda storheter kan eleverna inte göra uppskattningar eller avgöra rimlighet i mätuppgifter.
När det gäller mätning av tid har dygnet 24 timmar, timman 60 minuter och minuten 60 sekunder. Samtidigt mäter man i vissa situationer, t.ex. inom en del idrotter, sekunder i tiondelar och hundradelar. Man blandar alltså olika talbaser.
En del av diagnoserna i det här området förutsätter att eleven har god taluppfattning och behärskar grundläggande aritmetik.
Mätning. Alla diagnoser
Mätning av tid. MTi
Delområdet MTi omfattar följande fem diagnoser:
MTi1
Analog tid
MTi2
Tidsdifferens, analog tid
MTi3
Från analog till digital tid
MTi4
Delar av sekund
MTi5
Tidsdifferens, dagar mm
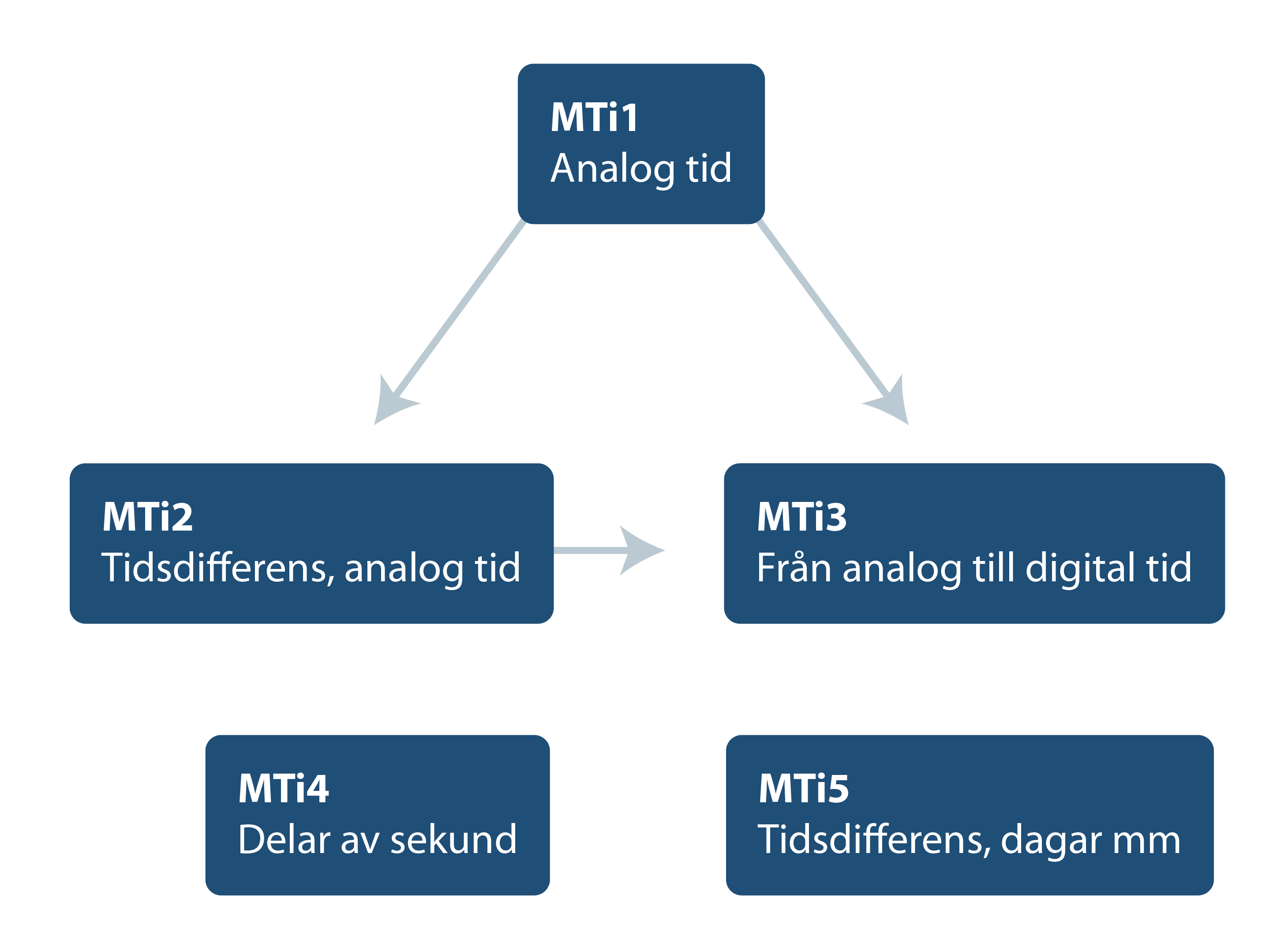
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan.
MTi2 bygger således på MTi1 och MTi3 på både MTi1 och MTi2 medan MTi 4 och MTi 5 är fristående och omfattar andra aspekter av tid och tidsuppfattning.
Didaktiska kommentarer till delområdet MTi
Att mäta tid skiljer sig en hel del från att mäta en sträcka eller en kropps massa. För det första är tid ett abstrakt och mer svårdefinierat begrepp. Tiden kan aldrig fångas och står aldrig stilla. För det andra bygger de viktigaste enheterna för tid inte på ett decimalsystem där enheterna byggs upp med hjälp av tiotal. Baserna är istället 60 sekunder per minut, 60 minuter per timma, 24 timmar per dygn och 7 dygn per vecka. När man kommer till antalet dagar per månad eller år är det ännu mer oregelbundet. Att man i vissa sammanhang såsom vid idrottstävlingar mäter sekunder i tiondelar och hundradelar gör situationen än mer komplicerad. De här diagnoserna omfattar i huvudsak två områden: att avläsa tid på en klocka och att bestämma tidsdifferenser inom ett dygn. Att avläsa en tidpunkt på ett digitalt ur är inte så svårt. Däremot kan det vara svårare att bestämma tidsdifferenser digitalt om man inte har någon analog urtavla att relatera tidpunkterna till. En nackdel med det analoga uret är dock att det inte ger tid i 24-timmars perspektiv.
Traditionella klockor visar analog tid samtidigt som det blivit allt vanligare att i olika sammanhang ange tid digitalt. Det är därför viktigt att eleverna förstår och kan använda sig av både analog och digital beskrivning av tid. Stoppur som används i samband med idrott anger tid på ett speciellt sätt. En tid som 2:14:55 ska tolkas som 2 minuter, 14 sekunder och 55 hundradels sekund. Man blandar således två olika talbaser. En viktig iakttagelse när det gäller beskrivning av tid är att den är kulturbunden. Vissa kulturer och religioner har en annan tideräkning och annan uppfattning om t.ex. dygnets början och slut än den västerländska. Detta bör uppmärksammas när man bedömer resultaten för en elev med annan kulturell bakgrund än den västerländska.
Mätning av massa. MMa
Delområdet MMa omfattar följande två diagnoser:
MMa1
Grundläggande mätning, massa
MMa2
Enhetsbyte, massa
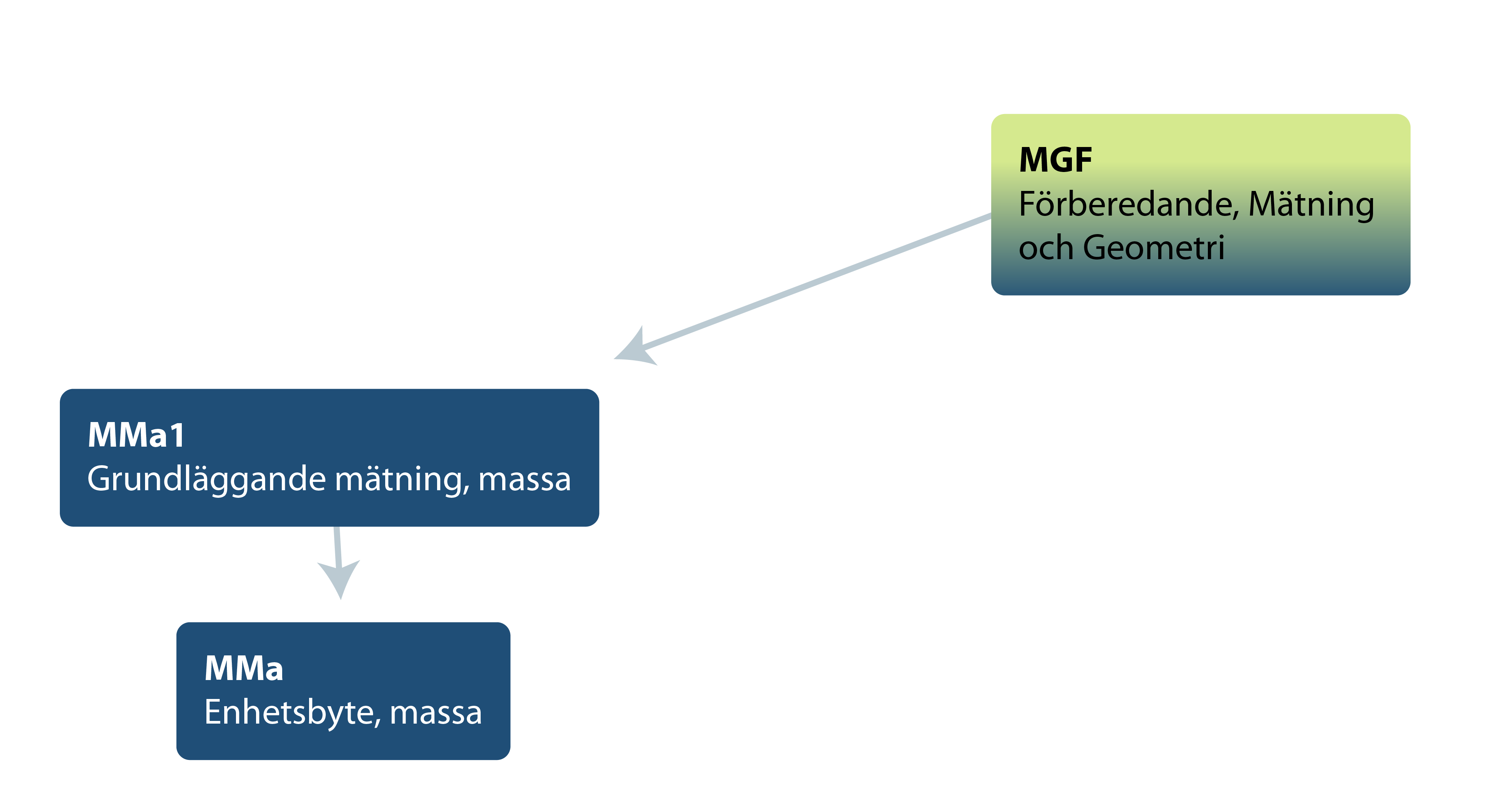
Diagnoserna inom delområdet är av två slag. På diagnos MMa1 ska eleverna kunna avläsa ett föremåls massa på två olika typer av vågar samt visa att de har en uppfattning om vilka enheter man kan använda för att ange vikten av några föremål, valda från deras vardag. På diagnos MMa2 ska eleverna kunna göra enhetsbyten mellan g, hg, kg och ton. Hälften av uppgifterna leder till enhetsbyten från eller till decimalform. Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan.
Didaktiska kommentarer till delområdet MMa
Mätning av massa handlar liksom övrig mätning om jämförelse. Jämförelsen kan göras mellan två föremål för att avgöra vilket som är lättast eller tyngst. Sådana uppgifter finns i MGF. I diagnoserna MMa1 och MMa2 sker mätningen genom jämförelse med standardiserade mått. Beroende på om det handlar om lätta eller tunga föremål, gäller det att välja en lämplig enhet för jämförelsen, alltså g, hg, kg eller ton. Samtidigt bör man vara medveten om att man i till exempel NO-undervisningen ofta uttrycker massa i kg, vilket då innebär att 1 g = 10-3 kg och 1 ton = 103 kg. Vägning sker i huvudsak på två olika sätt, med balansvåg eller med fjädervåg. Vid vägning med balansvåg sker en direkt jämförelse mellan en eller flera kända massor och en okänd massa. Vid vägning med en fjädervåg har det i förväg skett en kalibrering av fjädervågen med hjälp av kända massor. I dagens butiker är de flesta varor redan vägda och i de elektroniska vågar som används är mätandeprocessen dold för iakttagaren. Det är därför viktigt att man i skolan låter eleverna uppleva principerna för vägning. Elevernas uppfattning om detta är inte så lätt att diagnostisera med hjälp av skriftliga diagnoser. Vissa situationer, t.ex. vid jämförelse av massa, kräver enhetsbyten. En del sådana enhetsbyten förutsätter att eleverna behärskar decimaltal. 2 735 g kan då tolkas som 2 kg och 735 g = 2,735 kg eller som 27 hg och 35 g = 27,35 hg. Genom att koppla decimaltal till mätning av massa och enhetsbyten, kan eleverna ges en vardaglig förankring av decimaltalen och samtidigt ett stöd för mätning och enhetsbyten.
Mätning av längd. MLä
Delområdet MLä omfattar följande fyra diagnoser:
MLä1
Grundläggande mätning, längd
MLä2
Mätning, omkrets
MLä3
Enhetsbyte, längd
MLä4
Mätning, cirkeln
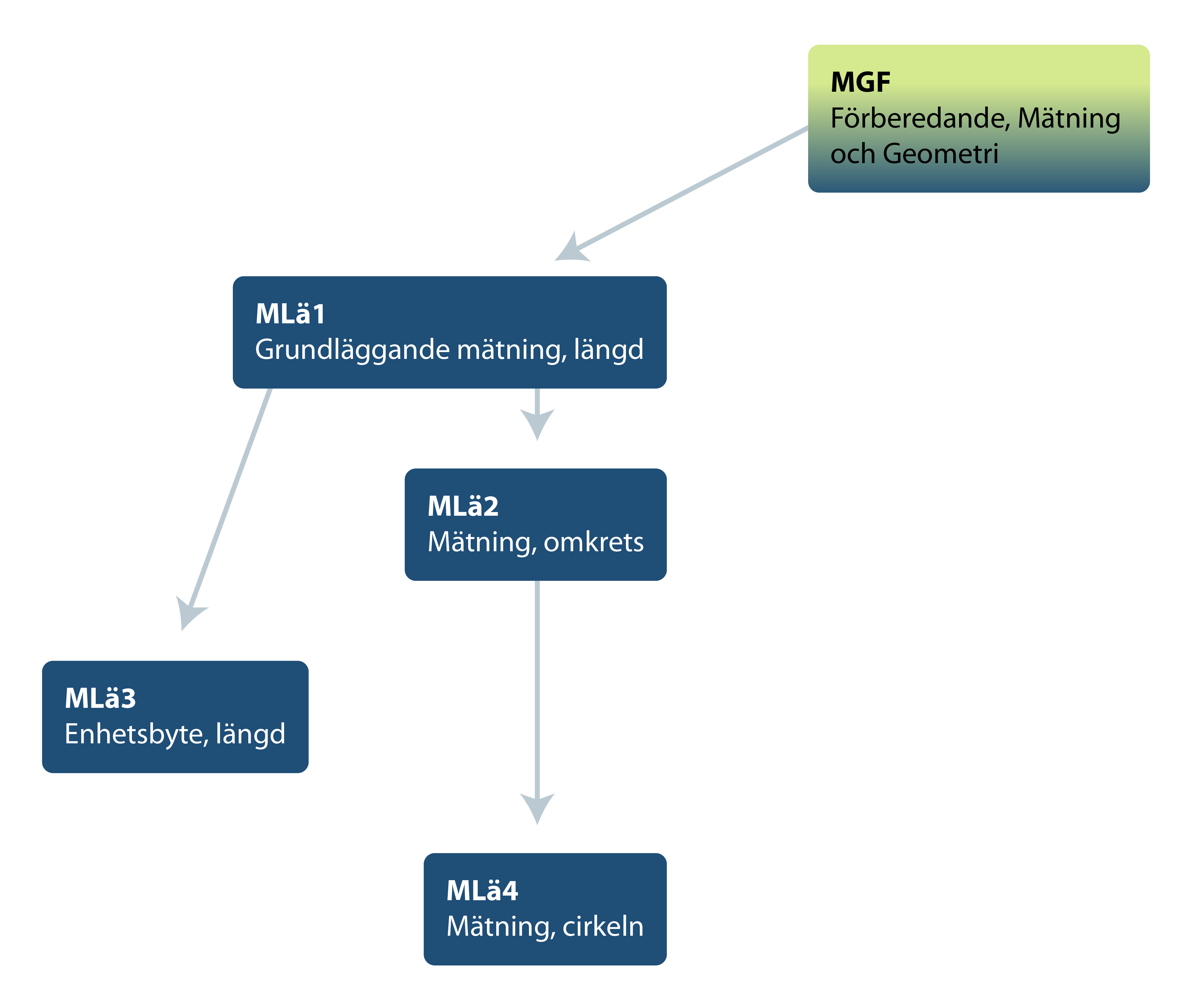
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Där framgår att Förberedande mätning och geometri (MGF) omfattar förkunskaper till mätning av längd. Det framgår också att MLä1 omfattar förkunskaper till diagnoserna MLä2 och MLä3. Diagnoserna MLä2 och MLä3 bygger således båda på MLä1, men saknar direkt koppling till varandra. Avsikten är att dessa tre diagnoser tillsammans ska täcka olika aspekter av längdmätning, alltså mätning och enhetsbyten med standardiserade mått.
Didaktiska kommentarer till delområdet MLä
När man mäter pennan i figuren kan det ske genom jämförelse på olika sätt. Man kan t.ex. jämföra pennan med Olles penna och finna att den är kortare. Vill man istället ha ett mått på pennan kan man jämföra den med en standardiserad enhet som 1 cm. Då finner man att pennan är lika lång som 8 enheter av längden 1 cm och säger att pennan är 8 cm lång.
För att förenkla mätningen använder man sig av graderade linjaler. Om pennan når från siffran 0 till siffran 8, så vet man att den är lika lång som 8 enheter av längden 1 cm. Det är i det här sammanhanget viktigt att påpeka att måttet 8 cm består av två delar, ett mätetal 8 och en enhet, cm. Elever som inte förstått mätandets idé, kan t.ex. inte mäta sträckor med hjälp av en avbruten linjal. De fokuserar nämligen på talen, inte på de enheter talen representerar. Det gäller alltså att göra klart för eleverna vad siffrorna på linjalen står för, nämligen att från 0 till talet 8 ryms det exakt åtta enheter av längden 1 cm. För att diagnostisera om eleverna har förstått mätandets idé, kan man låta dem mäta sträckor med en avbruten linjal. Det blir då tydligt om de fokuserar på enheten eller på de tal som står på linjalen. Beroende på om det handlar om korta eller långa föremål, gäller det att välja en lämplig enhet för jämförelsen, alltså mm, cm, dm, m eller km. Samtidigt bör man vara medveten om att man i till exempel NOundervisningen ofta uttrycker all längd i meter vilket då innebär att 1 mm = 10-3 m och 1 km = 103 m. Vissa situationer, till exempel jämförelse av längd, kräver enhetsbyten. En del sådana enhetsbyten förutsätter att eleverna behärskar decimaltal. 2 735 mm kan då tolkas som 2,735 m, 27,35 dm eller 273,5 cm. Genom att koppla decimaltal till mätning av längd och enhetsbyten, kan eleverna ges en vardaglig förankring av decimaltalen och samtidigt ett stöd för mätning och enhetsbyten. För att eleverna ska förstå principerna för enhetsbyten, och kunna generalisera dessa principer, bör de känna till prefixens innebörd, alltså att kilo betyder tusen, deci betyder tiondel, centi betyder hundradel och milli betyder tusendel. Vid mätning av omkrets är grundidén att addera längden av sidorna i t.ex. en rektangel. Passa då på att koppla detta till räknelagar och räkneregler. Om sidorna i en rektangel är 7 cm, 4 cm, 7 cm och 4 cm, så kan man teckna och beräkna detta som 2 ∙ 7 + 2 ∙ 4 cm = 2 ∙ (7 + 4) cm. För att kunna bestämma en cirkels omkrets måste man känna till proportionalitetsfaktorn π som beskriver relationen mellan cirkelns omkrets och dess diameter. Till en början kan man emellertid använda närmevärdet 3 för π. Detta kan förklaras om man skriver in en regelbunden sexhörning i en cirkel. Sexhörningens sida är då lika med radien, vilket ger att omkretsen är 3 gånger så stor som diametern. Eftersom cirkelns omkrets är något större än sexhörningens, så är cirkelns omkrets lite större än 3 gånger diametern.
Mätning av area. MAr
Delområdet MAr omfattar följande sju diagnoser:
MAr1
Grundläggande mätning, area
MAr2
Enhetsbyte, area
MAr3
Enkel areaberäkning
MAr4
Areaberäkning
MAr5
Enkel begränsningsarea
MAr6
Cirkelområdets area
MAr7
Begränsningsarea
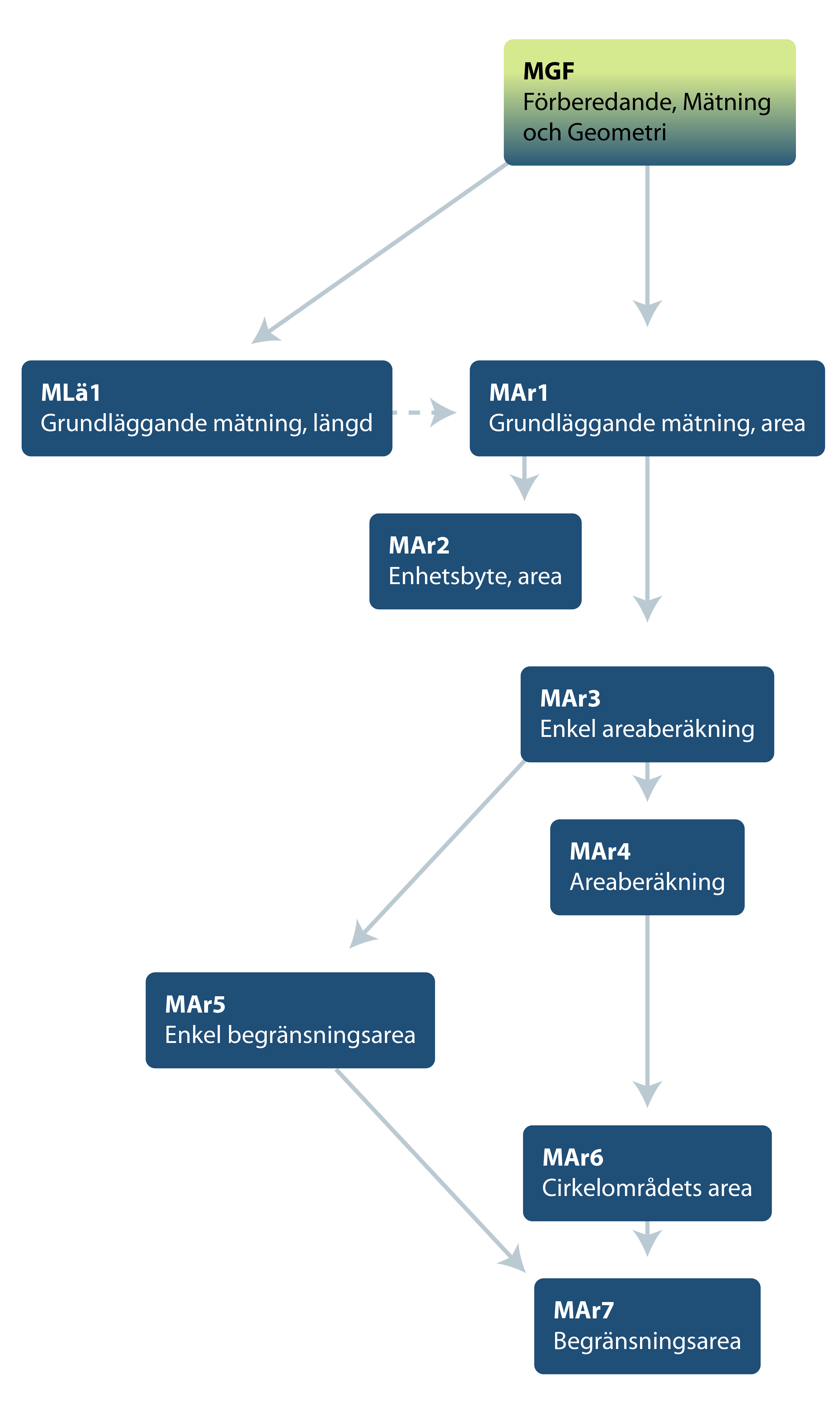
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Där framgår att MGF, förberedande mätning och geometri, omfattar förkunskaper till MAr. Detsamma gäller diagnosen MLä1 som behandlar de idéer som gäller för mätning av längd. Diagnoserna MAr1, MAr3, MAr4, MAr6 och MAr7 bygger på varandra i nämnd ordning och med stegrad komplexitet. MAr1, grundläggande areamätning, ger förkunskaper till MAr2,Enhetsbyten och MAr3, Enkel areaberäkning som ger förkunskaper till MAr5, Enkel begränsningsarea. Eftersom beräkning av area ofta omfattar en beräkning, förutsätter de flesta av diagnoserna att eleven har en god taluppfattning och behärskar grundläggande aritmetik.
Didaktiska kommentarer till delområdet MAr
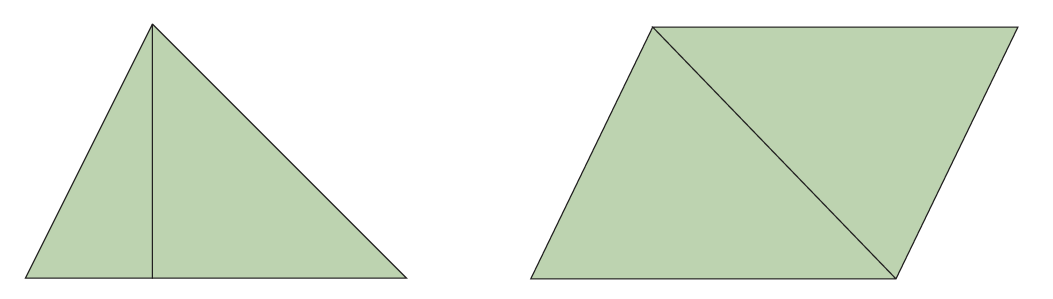
Att mäta area handlar om jämförelse. När man ska bestämma arean av en parallellogram, så jämför man i själva verket parallellogrammens area med arean av en rektangel med samma bas och höjd. På motsvarande sätt är triangelns area hälften av arean av en parallellogram med samma bas och höjd. Det är viktigt att eleverna förstår sådana geometriska samband och inte bara lär sig formler.
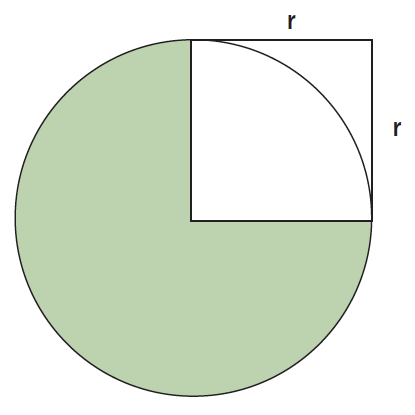
På motsvarande sätt kan man bestämma cirkelområdets area genom att jämföra denna med radiekvadratens area. Man finner att cirkelområdets area är drygt 3 gånger radiekvadratens area. Eleverna bör senare lära sig att proportionalitetskonstanten är ett irrationellt tal π ≈ 3,14. Eftersom radiekvadraten har arean r² blir cirkelområdets area π · r².
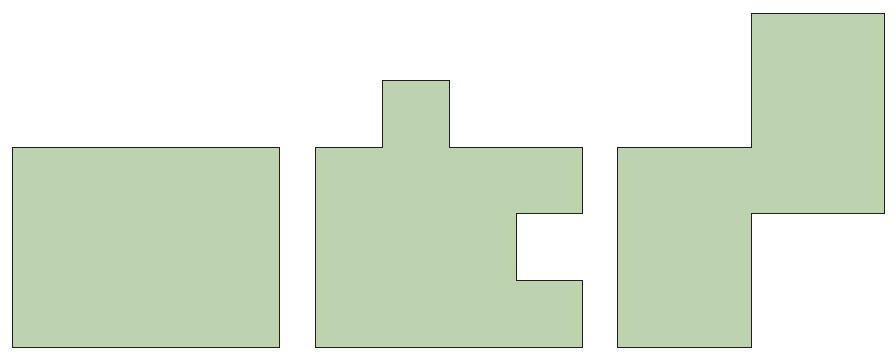
När man ”bevisar” detta för eleverna är det lämpligt att använda en metod som visar att detta värde på π är detsamma som vid mätning av omkrets, något som är lång ifrån självklart. En förutsättning för att eleverna ska kunna förstå idéerna bakom areamätning, är att de förstår konservering av area, alltså att arean av en figur inte förändras om man låter vissa delar av figuren byta plats. Följande figurer har alltså lika stor area.
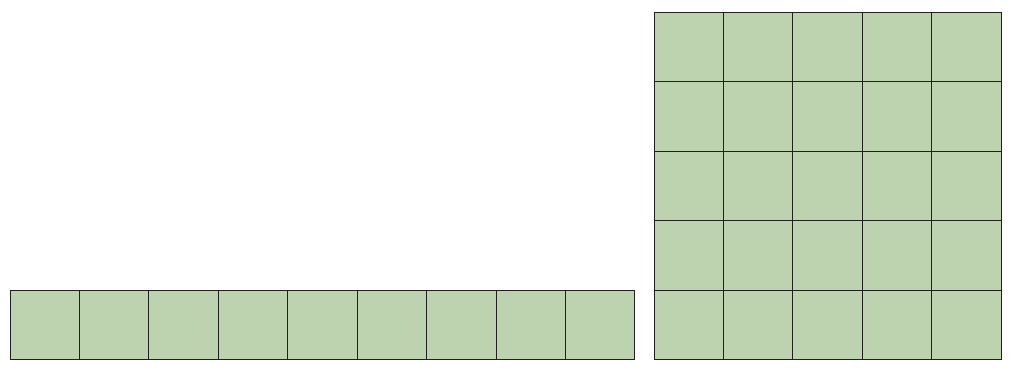
Det är också viktigt att eleven inser att arean av en figur inte är direkt beroende av figurens omkrets. Följande exempel visar två figurer som båda har omkretsen 20 cm, men där den ena arean är 9 cm² och den andra 25 cm².
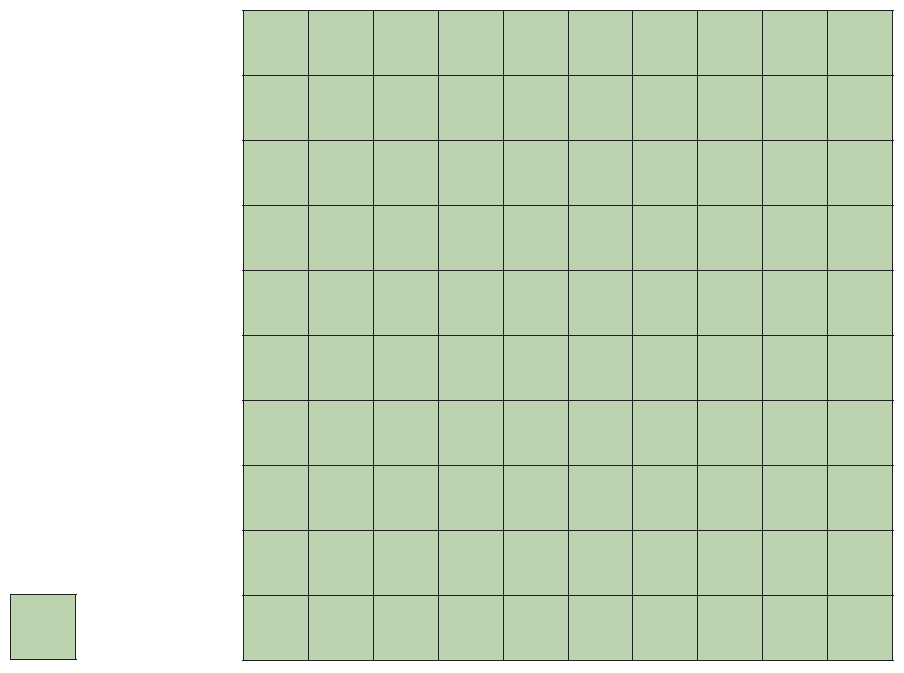
Ett annat exempel på detta är arean av en romb med sidan 4 cm, vars area kan variera mellan 0 och 16 cm2. Det är i det här fallet diagonalernas storlek som är avgörande. Diagnosen MAr2 handlar om enhetsbyten. Eleverna bör här göras uppmärksamma på att mönstret i det här fallet inte är linjärt utan kvadratiskt. Areaskalan är ju lika med kvadraten på längdskalan. Figurer av det här slaget är därför viktiga för att visa att det ryms 100 cm2 i en dm2.
När det gäller begränsningsarea bör eleverna göras uppmärksamma på terminologin. En kub är t.ex. uppbyggd av sex kvadrater. Om kvadratens sida är 3 cm, så är kubens kant 3 cm och dess sidor (egentligen sidoytor) 9 cm
Mätning av volym. MVo
Delområdet MVo omfattar följande sju diagnoser:
MVo1
Grundläggande mätning, volym
MVo2
Volym i vardagen
MVo3
Enhetsbyte, volym 1
MVo4
Enkel volymberäkning
MVo5
Volymberäkning 1
MVo6
Volymberäkning 2
MVo7
Enhetsbyte, volym 2
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Diagnosen MGF, förberedande mätning och geometri, innehåller uppgifter om mätandets idé och konservering av area och volym. Detta utgör förkunskaper till såväl MAr som till MVo. Det framgår också att MAr1, Grundläggande areamätning, omfattar förkunskaper till MVo1. På motsvarande sätt omfattar MAr2, enkla areaberäkningar, förkunskaper till MVo4 och MVo3. Diagnoserna MVo1, MVo4, MVo5 och MVo6, är successivt beroende av varandra och med ökad komplexitet. Diagnoserna MVo2 och MVo 3 handlar om enhetsbyten i vardagen respektive inom geometrin. Dessa har en koppling till MVo1 som handlar om grundläggande volymmätning.
Didaktiska kommentarer till delområdet MVo
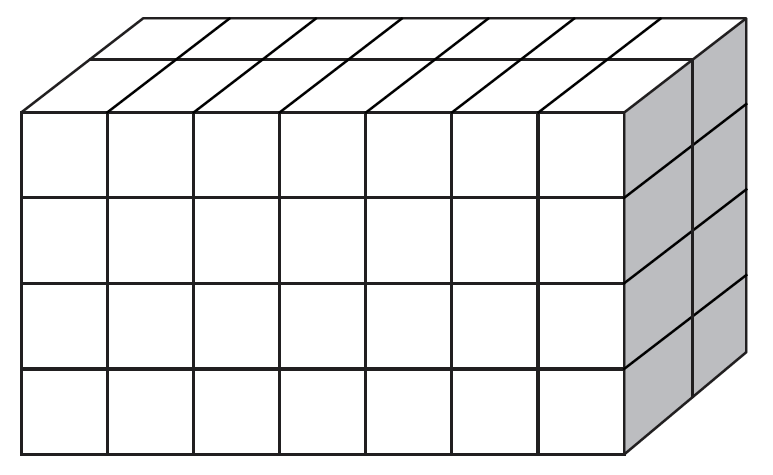
När det gäller mätning av kroppars volym inom geometrin, används samma idé som för mätning av area. Skillnaden är att man vid mätning av volym utgår från enhetskuber istället för enhetskvadrater. Det här rätblocket är uppbyggt av 7 · 2 · 4 enhetskuber med vardera volymen 1 cm³. Volymen är alltså 56 cm³.
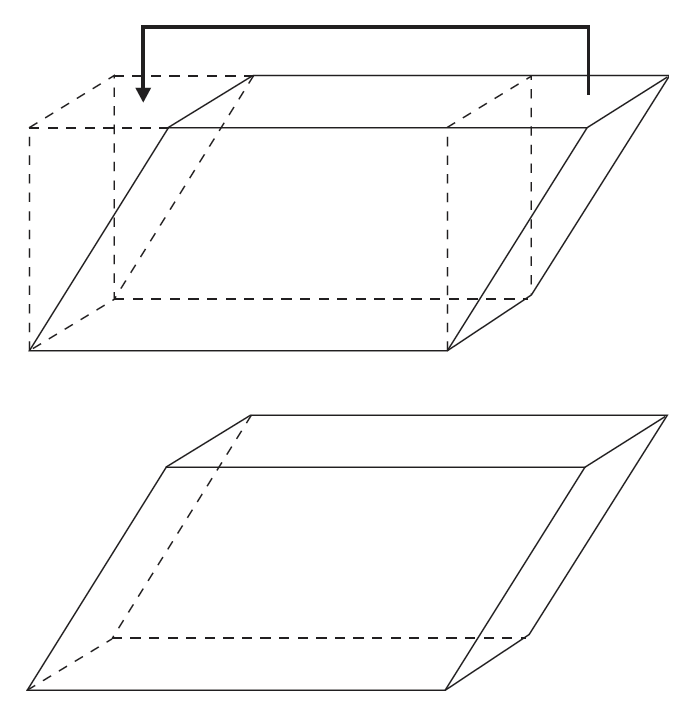
Vid mätning av volym är tekniken i stort sett densamma som för mätning av area. När man t.ex. ska mäta volymen av en parallellepiped så kan den jämföras med volymen av ett rätblock med samma basarea och samma höjd. Genom att dela parallellepipeden i två delar som på bilden och flytta den högra delen till vänster, kan parallellepipeden ”byggas om” till ett rätblock. Parallellepipeden har således samma volym som rätblocket.
Förståelse av detta är en förutsättning för att eleverna senare ska kunna förstå innebörden av formler som konens volym, \(\frac{B \cdot h}{3} \) (där B är basarean) eller klotets volym,\(\frac{4 \cdot π \cdot r^{3}}{3} \)
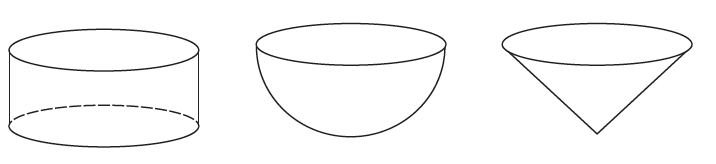
För att en elev ska kunna följa de här idéerna krävs det att eleven kan konservera volym, vilket innebär att ett givet föremåls volym inte förändras om man placerar om dess delar såsom i figuren. När det gäller mätning av volym förekommer det en rad formler som kan vara svåra att komma ihåg. Genom att gruppera dessa formler blir de betydligtfärre. Prismor, raka som sneda, är i själva verket cylindrar och följer samma formel som för cylindern. På motsvarandesätt är pyramiderna, raka som sneda, koner och följer samma formel som för konen. Om man dessutom känner till att volymerna för en cylinder, ett halvklot och en kon som har samma basyta och samma höjd förhåller sig 3 till 2 till 1, har man minskat behoven av formler till en enda.
När man i en vardagssituation ska bestämma volymen av något, t.ex. en vätska använder man en enkel idé. Man utgår då från standardmåttet en liter eller delar av en liter. Dessa mått utgår från en linjär skala. 1 liter = 10 dl och 10 cl = 1 dl osv. Ett undantag från detta är hushållsmåtten tsk och msk. Inom geometrin mäter man, som tidigare nämnts, volym på ett helt annat sätt, nämligen i m³, dm³, cm³ och mm³, där 1000 dm3= 1 m3, 1000 cm3 = 1 dm3 osv. Här används alltså en kubikskala som utgår från att 1 liter = 1 dm³. Som en konsekvens av detta är 1 cm³ = 1 ml medan 1 mm³ = 0,001 ml, något som ibland skapar förvirring. Det här tas inte upp i dessa diagnoser. Däremot behandlar diagnos MVo1 förkunskap till detta.