Talmönster och algebra. TA
Talmönster och algebra. TA
Talmönster och algebra. TA
Diagnoserna i området avser att kartlägga om eleverna kan upptäcka talmönster samt på olika sätt bearbeta algebraiska uttryck och ekvationer. Förståelse av koordinatsystem och grafer ingår också i området.
Området består av följande fyra delområden:
TAt
Talföljder och talmönster
TAu
Algebraiska uttryck
TAe
Ekvationer
TAg
Koordinatsystem och grafer
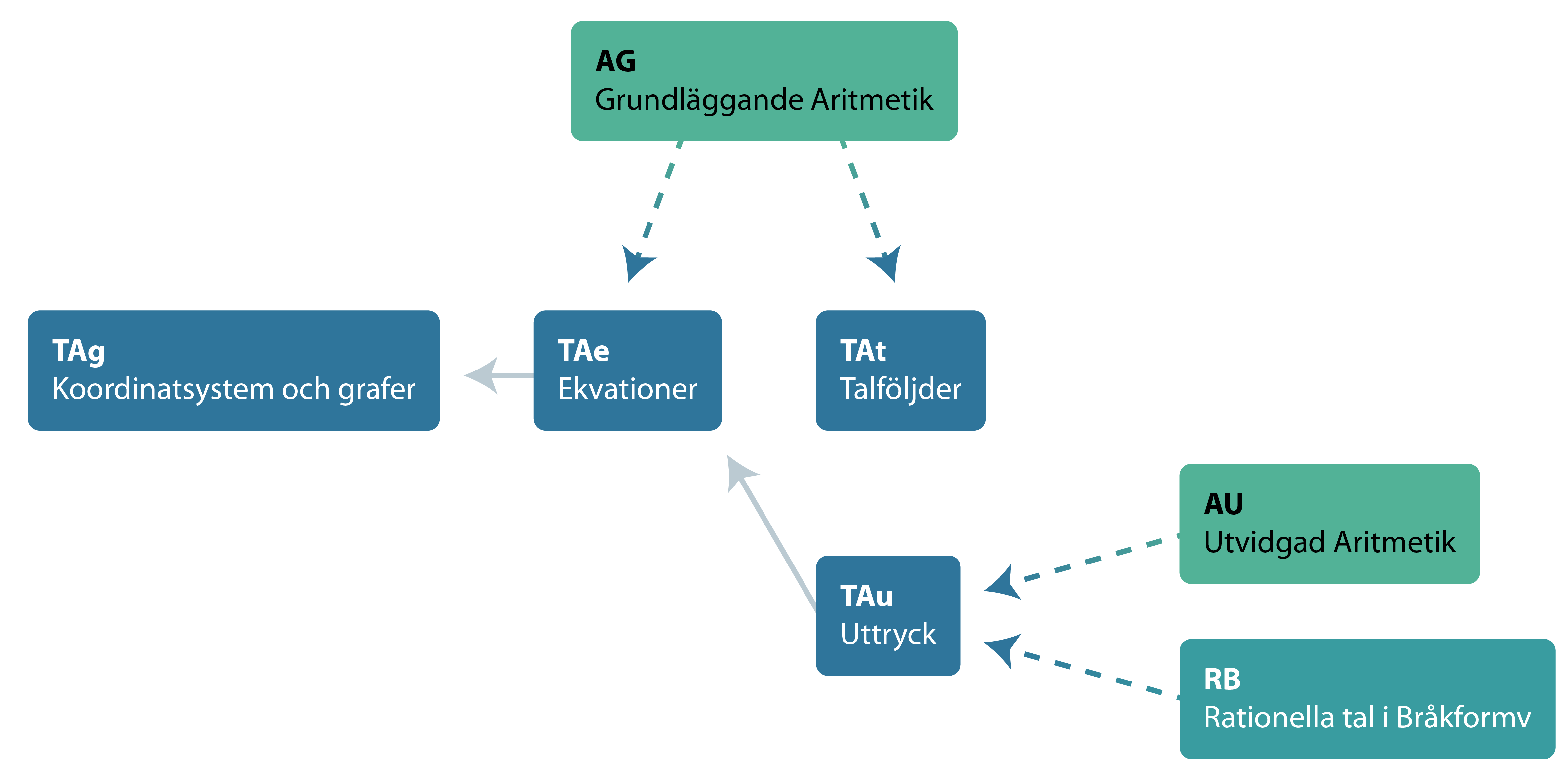
Sambandet mellan delområdena ser ut så här:
Strukturschemat visar att grundläggande aritmetik, AG omfattar förkunskap till Talföljder och talmönster, TAt och till Ekvationer, TAe. Dessutom behövs förkunskaper från Utvidgad aritmetik, AU och Rationella tal i bråkform, RB för att arbeta inom Algebraiska uttryck, TAu. Det finns klara samband, en förkunskapsstruktur, mellan olika diagnoser såväl inom som mellan delområden. Detta kan emellertid inte uttryckas entydigt med pilar mellan delområdena utan detaljer framgår av strukturschemat för respektive delområde.
Området Talmönster och algebra i relation till syfte och centralt innehåll i kursplanen i matematik
Med hjälp av diagnoserna inom detta område kan man ta reda på om elever har byggt upp ett begreppsförråd och ett verktygsförråd inom främst algebra som behövs för att utveckla förmågan att:
- formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder,
- använda och analysera matematiska begrepp och samband mellan begrepp,
- välja och använda lämpliga matematiska metoder för att göra beräkningar och lösa rutinuppgifter
- föra och följa matematiska resonemang, och
- använda matematikens uttrycksformer för att samtala om, argumentera och redogöra för frågeställningar, beräkningar och slutsatser
En väsentlig del av den grundläggande matematikundervisningen bygger på räknelagar och räkneregler. Genom att tidigt synliggöra detta i undervisningen underlättar man för eleverna att utveckla förmågan att kunna resonera, bygga begrepp och se samband samt att senare kunna generalisera den grundläggande aritmetiken till andra områden. Genom att tala matematik ska eleven få hjälp att se olika beräkningsmetoders styrkor och svagheter samt lära sig att använda de matematiska uttrycksformerna, inom området, på ett korrekt sätt.
Diagnoserna ger eleven möjlighet att visa kunskaper inom följande centrala innehåll:
Det centrala innehållet som behandlar rationella tal finner man under rubrikerna Algebra och Samband och förändring.
Årskurs 1–3
Algebra:
- Matematiska likheter och likhetstecknets betydelse
- Hur enkla mönster i talföljder och enkla geometriska mönster kan konstrueras, beskrivas och uttryckas.
Det är viktigt att eleven tidigt får syn på de generella regler som gäller för räkning med naturliga tal. Dessa regler ska senare generaliseras till nya områden. Det samma gäller för talföljder och geometriska mönster som till en början ska kunna tolkas informellt och senare behandlas formellt. I kunskapskraven för godtagbara kunskaper i årskurs 3 finns följande: – Eleven kan hantera enkla matematiska likheter och använder då likhetstecknet på ett fungerande sätt. Likhetstecknet är centralt inom matematikens uttrycksformer. Därför är det angeläget att eleven tidigt lär sig använda likhetstecknet korrekt. Ett annat kunskapskrav gäller: Eleven kan föra och följa resonemang om val av metod och räknesätt ………… mönster i talföljder genom att ställa och besvara frågor som i huvudsak tillhör ämnet. Elev ska således kunna identifiera och beskriva enkla strukturer inom matematiken.
Årskurs 4–6
Algebra:
- Obekanta tal och deras egenskaper samt situationer där det finns behov av att beteckna ett obekant tal med en symbol.
- Enkla algebraiska uttryck och ekvationer i situationer som är relevanta för eleven.
- Metoder för enkel ekvationslösning.
- Hur mönster i talföljder och geometriska mönster kan konstrueras, beskrivas och uttryckas.
Samband och förändring:
- Koordinatsystem och strategier för gradering av koordinataxlar.
I kunskapskraven i slutet av årskurs 6 finns ingen direkt beskrivning i relation till det centrala innehållet men det är viktigt att eleven har tagit ett först steg från räkning till algebra och bekantat sig med olika variabler och uttrycksformer. Elev ska kunna identifiera och beskriva strukturer inom matematiken och uttrycka dessa i till exempel formler.
Koordinatsystemet förekommer i en rad informella och formella sammanhang såsom på kartor och i diagram detta ger goda möjligheter att konkretisera samband och förändring som inledning till formell behandling.
Årskurs 7–9
Algebra:
- innebörden av variabelbegreppet och dess användning i algebraiska uttryck, formler och ekvationer
- metoder för ekvationslösning
Samband och förändring: - funktioner och räta linjens ekvation.
Inte heller i kunskapskraven i slutet av årskurs 9, finns någon direkt beskrivning i relation till det centrala innehållet, men användningen av variabler innebär ett viktigt steg från räkning till algebra. Inledningsvis kan det gälla att sätta in olika värden på variabeln och tolka uttryck. Därefter bör eleven själv, utgående från givna problem, kunna skriva motsvarande uttryck eller ekvation. Eleven bör kunna lösa olika typer av ekvationer med generella lösningsmetoder. Genom att rita grafer till en funktion blir det ofta enklare att tolka funktionen och se intressanta egenskaper. Eleven bör därför kunna gå fram och tillbaka mellan en funktion och dess graf.
Didaktiska kommentarer till området
Algebra är den gren av matematiken där man studerar grupper, ringar och kroppar. Detta handlar bland annat om vilka räkneregler och räknelagar som gäller inom olika talområden. Det innebär att redan den mest grundläggande aritmetiken i själva verket handlar om algebraiska strukturer.
När man inom den grundläggande aritmetiken studerar de grundläggande räknelagarna såsom att 2 + 7 = 7 + 2, (7 + 8) + 2 = 7 + (8 + 2) eller 6 ∙ (3 + 7) = 18 + 42, så gäller detta enbart lokalt, i just dessa sammanhang. Vad algebran däremot handlar om är reglernas generella giltighet, t.ex. att även 1/3 ∙ √2 = √2 ∙ 1/3, (√5 + π) + √3 = √5 + (π + √3). Det är för att uttrycka sådana generella samband man använder sig av variabler såsom a + b = b + a och (a + b) + c = a + (b + c). Notera samtidigt att aritmetiken kan användas för att konkretisera algebran.
Några av de vanligaste algebraiska begreppen i skolan är ekvation och olikhet, vilka samtidigt används för effektiva metoder vid problemlösning. Det är angeläget att eleverna tidigt förstår innebörden i en ekvation, alltså att det är en utsaga och att lösandet av ekvationen handlar om att undersöka vilka värden på variabeln (oftast x) som gör utsagan sann. En del ekvationer kan lösas genom ren gissning, men detta är inte målet, utan eleverna bör lära sig generella metoder att lösa ekvationer och olikheter. Detta ska emellertid inte hindra elever med en bra känsla för matematik från att finna smarta genvägar till en lösning. Detta kan t.ex. handla om att lösa en andragradsekvation som
\( x^{2}\) − 5x + 6 = 0 genom att studera rötternas summa (alltså 5) och rötternas produkt (alltså 6) och därigenom direkt se lösningarna x = 2 och x = 3.
Detta som en följd av att räkneregler använts. Studera ekvationen (x − 2)(x − 3) = 0, där är (x − 2) = 0 eller (x − 3) = 0 och ekvationen har rötterna x = 2, x = 3.
Ekvationen ovan kan efter utförd multiplikation skrivas som \( x^{2}\) − 5x + 6 = 2. Man kan nu se att koefficienten för x-termen är lika med rötternas summa, −5 = −(2 + 3). Den konstanta termen 6 är lika med produkten av rötterna 2 ∙ 3.
En förstagradsekvation kan ha oändligt många lösningar eller sakna lösning. Detta bör redas ut med eleverna. Eleverna bör även vänjas vid att alltid sätta in förmodade lösningar i ekvationen för att se att om lösningen satisfierar ekvationen, alltså om utsagan blir sann.
En viktig period i matematikens historia var när man på 1600-talet dels utvecklade algebran, dels knöt ihop algebran med geometrin genom att åskådliggöra algebraiska uttryck och utsagor i ett koordinatsystem. Detta innebär samtidigt att man, genom att avbilda ekvationer i ett ekvationssystem, kan lösa ekvationssystem grafiskt. Man kan med hjälp av grafer i ett koordinatsystem diskutera antal lösningar till linjära ekvationssystem.
Inom matematiken finns det en rad talföljder och talmönster, som dyker upp i flera olika sammanhang. För den som är bekant med dessa talmönster är det ofta enkelt att se och förutsäga lösningar på matematiska problem. Sådana mönster är de udda talen, kvadrattalen, triangeltalen, Pascals triangel m.fl. Talföljder och mönster av det här slaget kan uttryckas på olika sätt, mer eller mindre formellt, men målet är att de flesta elever ska uppfatta exempelvis att de udda talen kan skrivas som 2n − 1 och triangeltalen som n(n + 1)/2.
Talmönster. Alla diagnoser
Talföljder och talmönster. TAt
Delområdet TAt omfattar följande fem diagnoser.
TAt1
Talföljder 1
TAt2
Talföljder 2
TAt3
Talmönster 1
TAt4
Talmönster 2
TAt5
Geometriska mönster
Arbetet med de här diagnoserna förutsätter att eleverna har förkunskaper från delområdet Grundläggande aritmetik, AG.
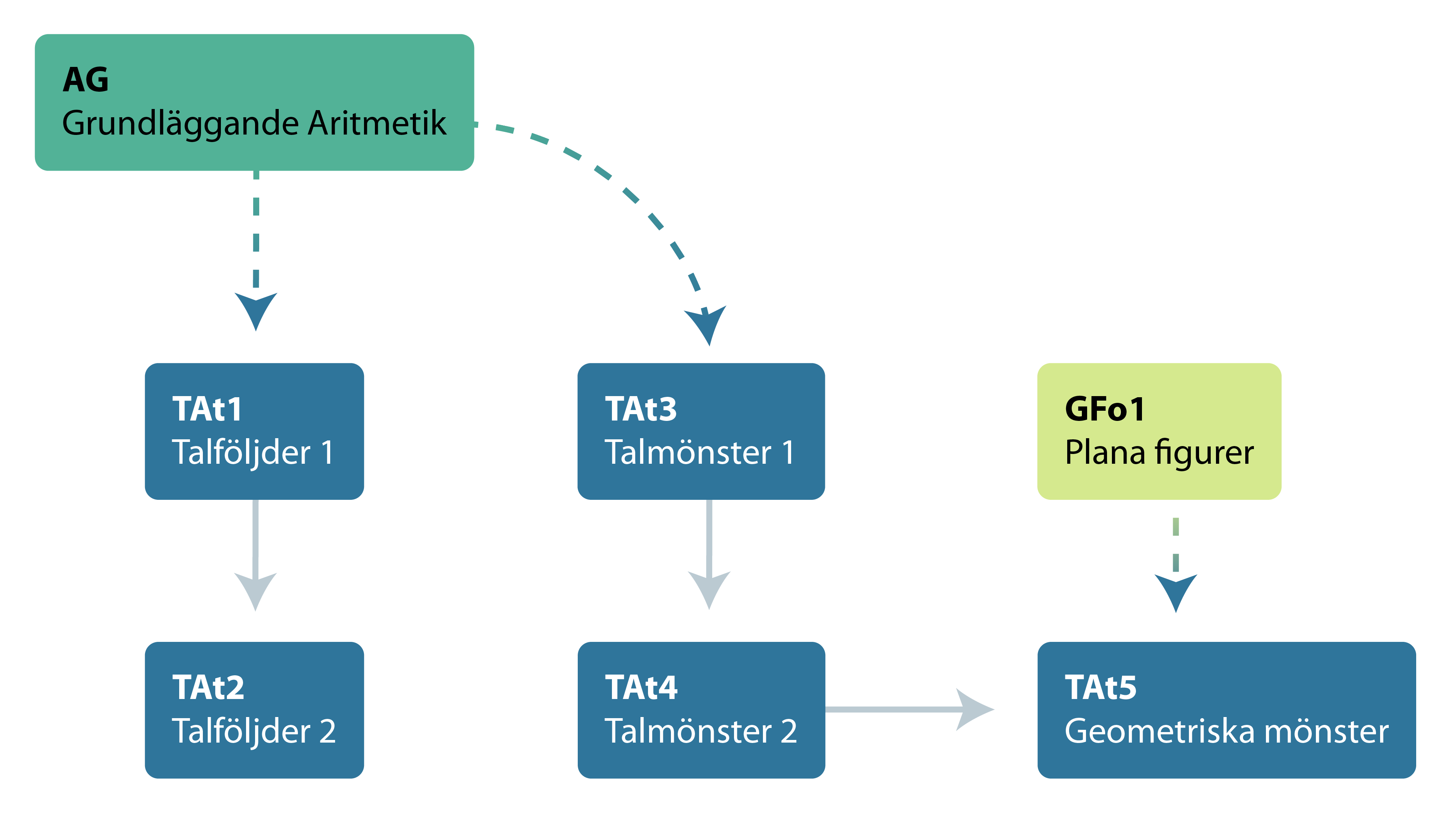
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Där framgår att TAt1 är förkunskap till TAt2 och att TAt3 är förkunskap till TAt4, som i sin tur är förkunskap till TAt5. Av schemat framgår också att GFo1, Plana figurer, är förkunskap till TAt5.
Didaktiska kommentarer till delområdet
Matematik handlar till stor del om att utnyttja kända mönster hos tal och att använda dessa mönster på ett lämpligt sätt. En förutsättning för detta är att eleven kan känna igen och utnyttja sådana mönster. Senare kan denna kunskap överföras till algebraiska mönster och bidra till elevens förståelse av algebra. När det gäller talmönster har många elever en informell och intuitiv uppfattning. Dessa intuitiva kunskaper måste emellertid formaliseras om de ska kunna användas för att lära matematik och fördjupa det matematiska kunnandet.
Att upptäcka talmönster handlar om att känna igen relationer mellan tal och generella samband och räknelagar. Ett centralt innehåll inom algebran är hur enkla mönster i talföljder … kan konstrueras, beskrivas och uttryckas. Exempel på sådana talmönster är de udda och de jämna talen samt tiotalen, alltså
- 1,3,5,7,9,…
- 2,4,6,8,10…
- 10, 20, 30, 40, 50, ….
Man kan till exempel diskutera med eleverna om vilket tal som är nästa tal i en given talföljd eller vilket tal som fattas i en talföljd. Eleverna ska då öva sig på att uttrycka detta med ett adekvat språk och att språkligt beskriva hur talföljden är uppbyggd.
En annan talföljd som ofta dyker upp inom matematiken är triangeltalen, 1, 3, 6, 10, 15, … som bildas genom att man börjar med 1 och därefter successivt lägger till 2, 3, 4, 5… Man får då följden 1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4 osv. En praktisk tillämpning av triangeltalen är att den beskriver hur många par man kan välja ut bland 2, 3, 4, 5 respektive 6 personer. Anledningen till att talen kallas för triangeltal, framgår av följande illustration.
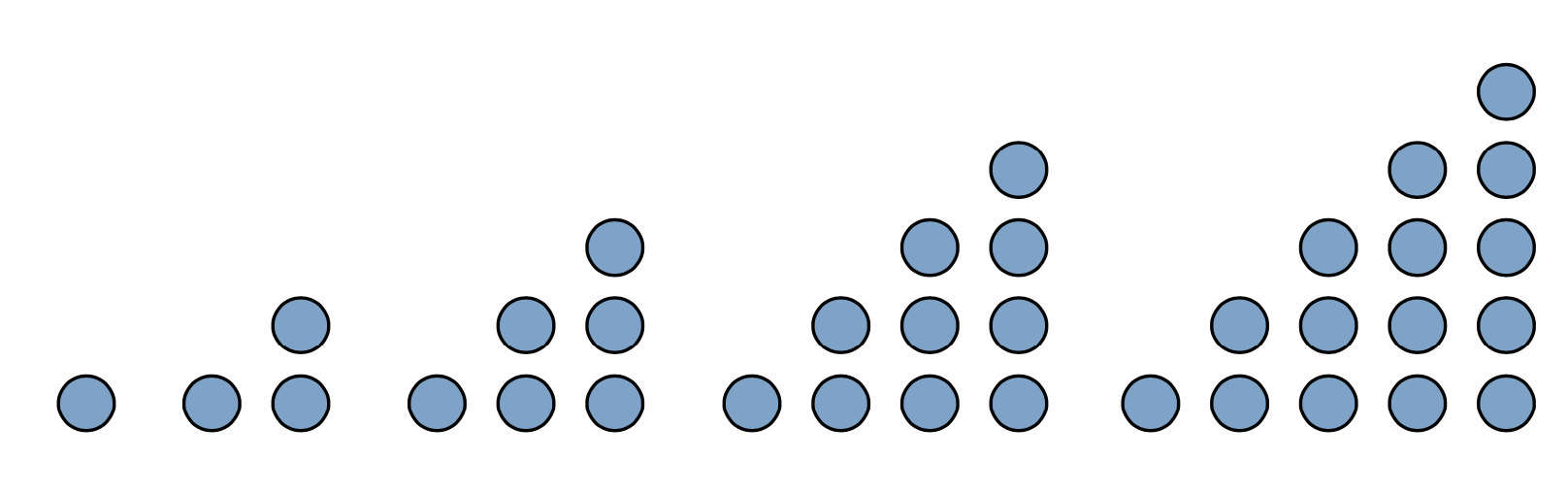
Man kan sedan fortsätta med kvadrattalen 1, 4, 9, 16, 25 … Om man beskriver multiplikationstabellen som en kvadrat, så finner man kvadrattalen som en diagonal i multiplikationstabellen.
Som exempel på användning av räknelagarna kan man arbeta med aritmetiska talföljer, alltså sådana där differensen mellan två på varandra följande termer är konstant, t.ex. 1, 3, 5, 7, 9, 11, 13, 15, 17, 19.
För att beräkna summan av dessa termer, alltså 1 +
3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 grupperar vi om dem så här (1 + 19) + (3 + 17) + (5 + 15) + (7 + 13) + (9 + 11) vilket ger 5 par med summan 20, alltså totalt 5 ∙ 20 = 100, där 5 är halva antalet termer och 20 är summan av den första och den sista termen. Detta handlar om matematiska mönster, former och samband.
En geometrisk serie är en serie där kvoten av två på varandra följande tal är konstant. Till exempel är serien 1, 1/2, 1/4, 1/8…. exempel på en geometrisk serie.
Denna series summa (1 + 1/2 + 1/4 +….) kan fås genom en geometrisk lösning:
Rita en sträcka som är 2 dm lång på en tallinje. Dela först sträckan på mitten. Dela därefter den högra delen på mitten. Genom att addera de två delarna får man 1 + 1/2
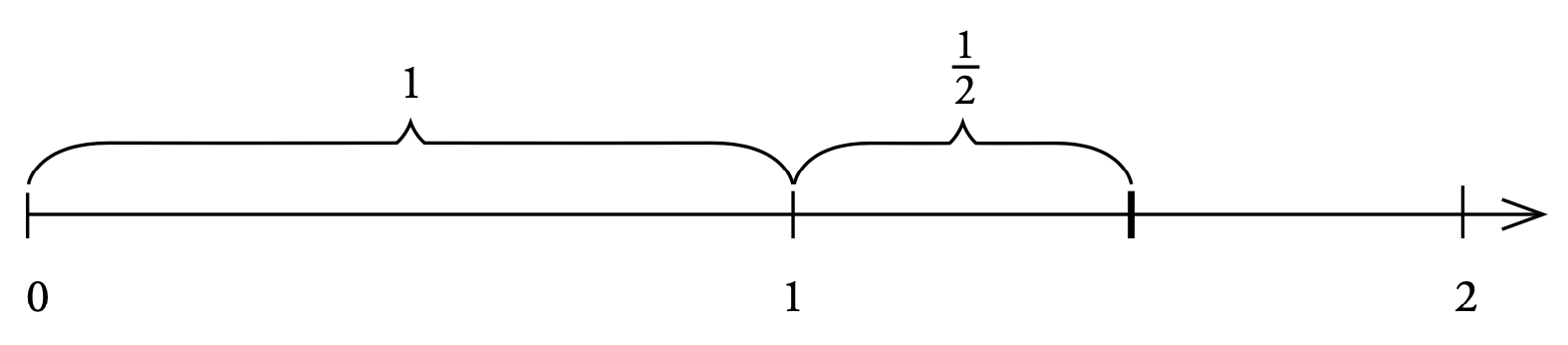
Man fortsätter nu att successivt halvera den sträcka som återstår fram till talet 2. Efter ytterligare två steg ser resultatet ut så här:
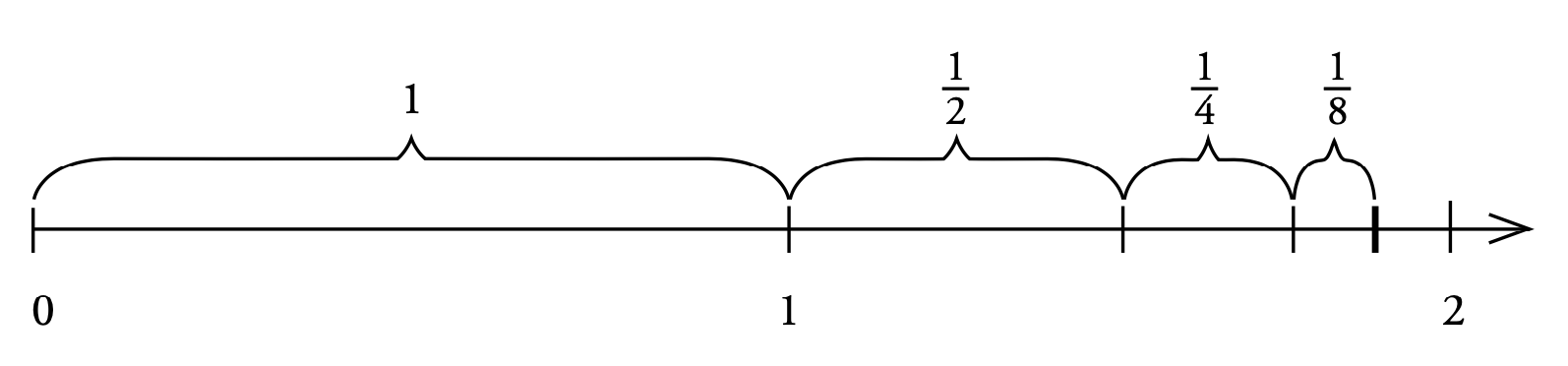
Den kraftigaste markeringen svarar nu mot summan 1 + 1/2 + 1/4 +1/8. Processen att successivt halvera den kvarstående sträckan illustrerar att ju fler termer man adderar desto närmare kommer man talet 2 som är seriens summa.
De flesta av diagnoserna i området förutsätter att eleverna har en god taluppfatttning och behärskar grundläggande aritmetik.
Algebraiska uttryck. TAu
Delområdet TAu omfattar följande fem diagnoser.
TAu1
Enkla uttryck
TAu2
Uttryck
TAu3
Förenkling av uttryck
TAu4
Multiplikation av binom
TAu5
Förenkling av rationella uttryck
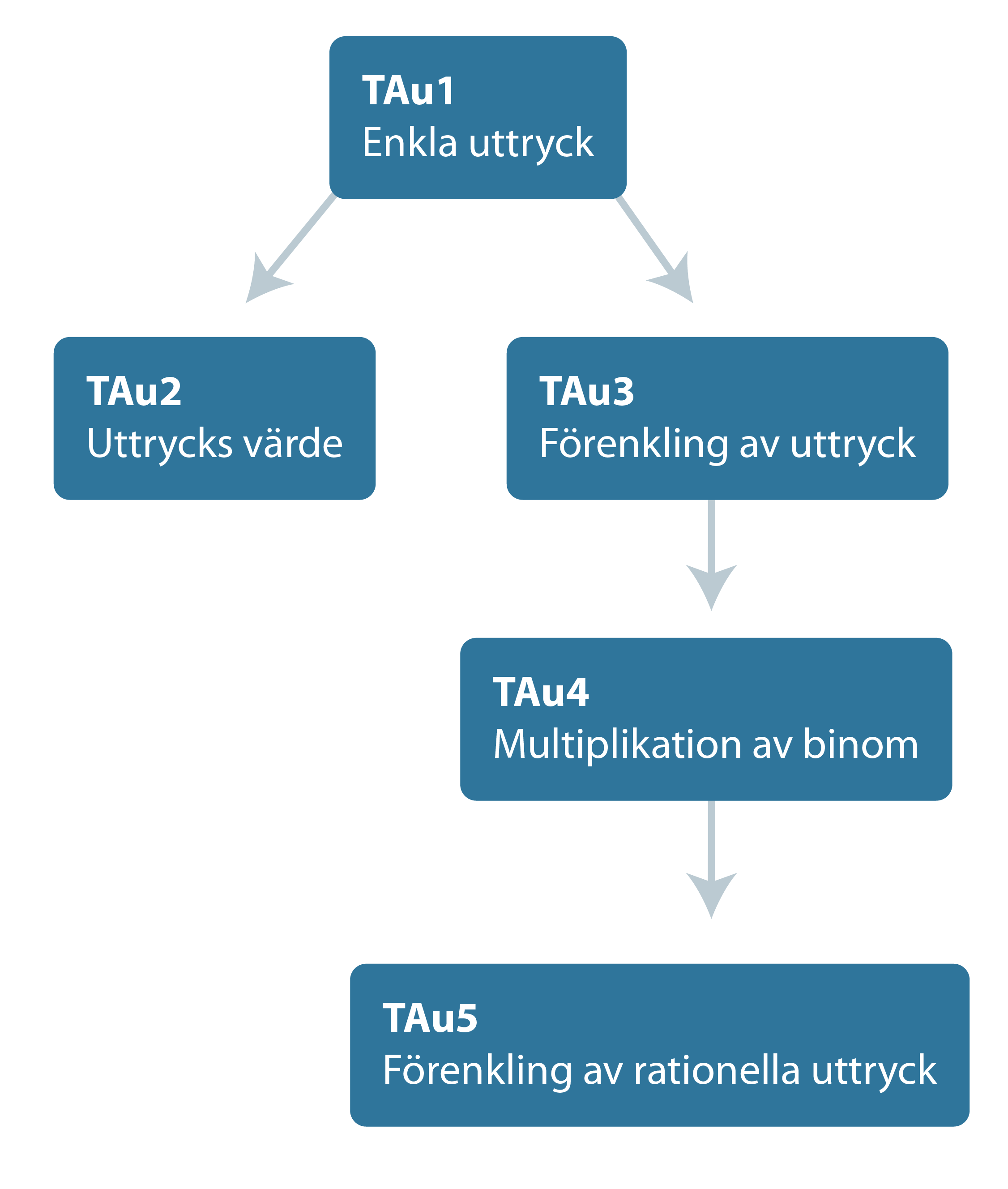
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Där framgår att TAu1 är förkunskap till TAu2 och TAu3, samt att TAu3 är förkunskap till TAu4, som i sin tur är förkunskap till TAu5. TAu4, multiplikation av binom, utgör även förkunskaper till TAe6 andragradsekvationer. Självklart finns det också ett samband med diagnoserna inom exempelvis AU, Utvidgad aritmetik, och RB, Tal i bråkform. Dessa samband är dock inte utritade i strukturschemat.
Didaktiska kommentarer till delområdet TAu
Eleverna ska så småningom kunna formulera en ekvation utifrån en problemlösningssituation, lösa ekvationen och sedan tolka resultatet i förhållande till det ursprungliga problemet. Detta innebär att eleven måste kunna uppfatta problemets struktur och uttrycka det algebraiskt samt kunna bearbeta uttrycket och lösa ekvationen. I detta delområde testas elevens förmåga att bearbeta algebraiska uttryck.
För att förstå algebraiska uttryck kan man t.ex. koppla detta till geometrin. Formeln för rektangelns area kan då skrivas A = b ∙ h. Här kan man börja med att sätta in värden på b och h. I nästa steg kan man betrakta följande rektangel.
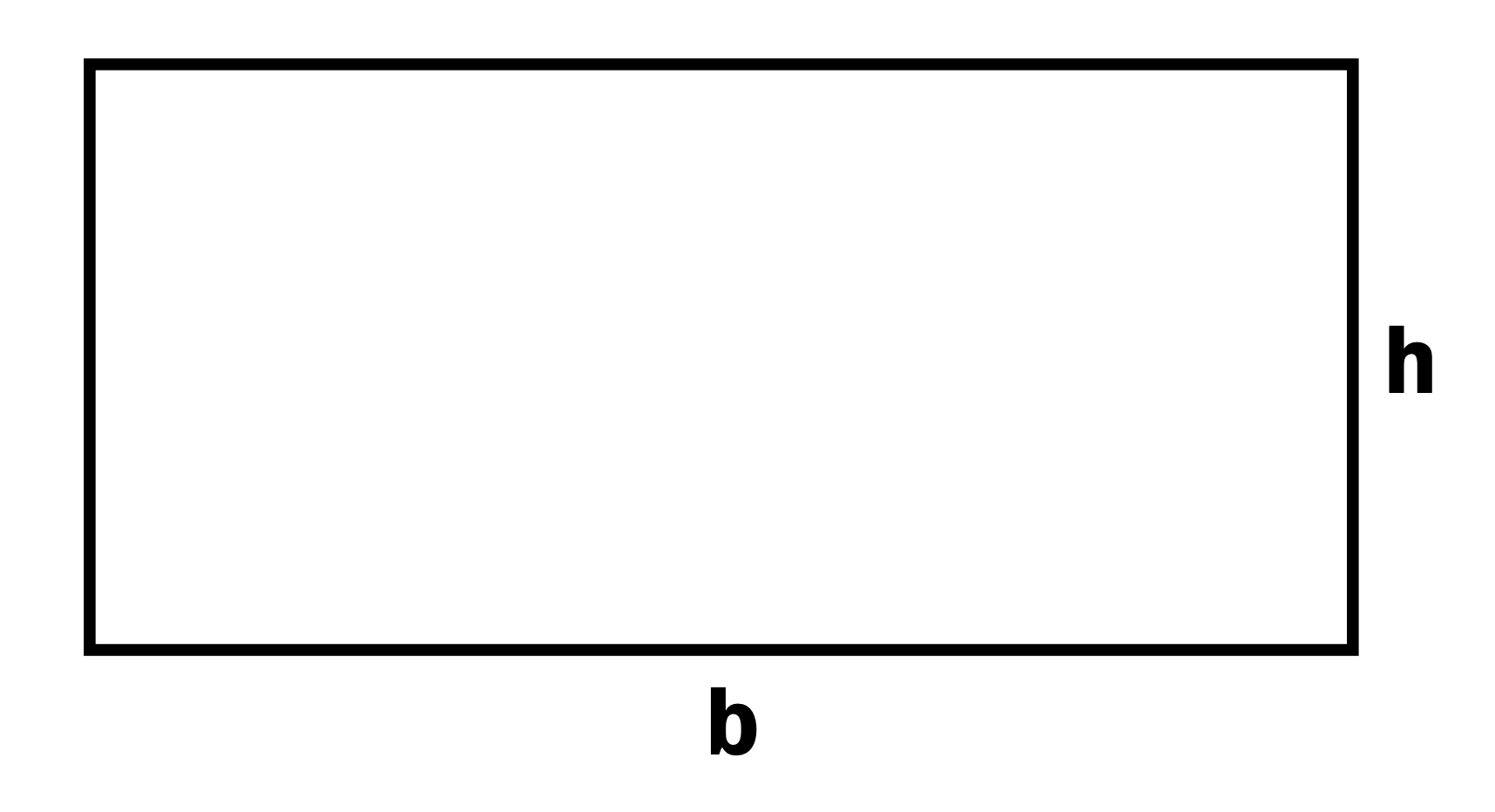
För att bestämma rektangelns omkrets kan man först addera b + h + b + h. Men man kan även addera i ordningen b + b + h + h vilket kan skrivas 2 ∙ b + 2 ∙ h. Detta kan också skrivas 2b + 2h.
Man kan nu införa enkla parenteser. Detta kan återigen knytas till rektangelns omkrets genom att man först beräkna halva omkretsen alltså b + h. Detta kan skrivas som (b + h) för att markera att man betraktar det som ett tal. Hela omkretsen, som är dubbelt så
stor kan då skrivas 2 ∙ (b + h) vilket även kan tecknas 2(b + h). Eleverna bör nu också kunna utföra förenklingar såsom 3a + 4a = 7a. I ett första steg bör detta förtydligas som 3a + 4a = (a + a + a) + (a + a + a + a) = a + a + a + a + a + a + a = 7a. Även uttryck som 7a − 4a och 2a + 5b + 3a − 2b bör tas upp och diskuteras.
Arbetet med parenteser kan utföras i två steg. De enklaste varianterna är av typen 3x ± (4 + x). Står det + i parentesen kan uttrycken tolkas med ”både och”: 3x + (4 + x) tolkas som att man ska addera både 4 och x vilket ger 3x + 4 + x
3x − (4 + x) tolkas som att man ska subtrahera både 4 och x vilket ger 3x − 4 − x.
En förutsättning för att eleverna ska komma vidare inom algebran är att de har en förståelse för vad subtraktion med ett negativt tal innebär. Om eleven har förstått att a − b = a + (-b), alltså att en subtraktion av ett tal alltid kan ersättas med en addition av det motsatta talet kan 3x + (4 − x) tolkas som 3x + [4 + (−x)]. Detta ger 3x + [4 + (−x)] = 3x + 4 + (−x) = 2x + 4.
Vid förenkling av algebraiska uttryck i rationell form kan jämförelse med förenkling av bråkuttryck med naturliga tal göras.
Ett bråk som \(\frac{9}{15}\) kan skrivas som \(\frac{3 \cdot 3}{5 \cdot 3}\), vilket kan förkortas med 3 till \(\frac{3}{5}\). Samma idé kan även användas för att visa att \( \frac{a^5}{a^3} = a^2 \). Man skriver då om \( a^5 / a^3 \) som a ∙ a ∙ a ∙ a ∙ a/a ∙ a ∙ a och förkortar med a tre gånger.
Man bör redan nu förbereda eleverna inför arbetet med binom. Ett binom som (2a + b) står för ett tal på samma sätt som a eller 7 gör det. Det betyder att (2a + b)(2a − b)/(2a+b)kan förkortas med (2a + b) eftersom samma tal (2a + b) finns i både täljare och nämnare. Detta ger resultatet (2a − b), på samma sätt som a ∙ b/a kan förkortas med a vilket ger resultatet b.
En multiplikation av typen a ∙ (b ± c) är relativt enkel. Innbörden är att både b och c ska multipliceras med a. Lika enkelt är det att utföra multiplikationen (−a) ∙ (b + c) som på motsvarande sätt ger (−a) ∙ b + (−a) ∙ c = (−ab) + (−ac) eller om man så vill −(ab + ac).
För att multiplicera två binom såsom (2x − 4) ∙ (x + 3) kan man först dela upp multiplikationen i två steg. Innebörden är att talet (2x − 4) ska multipliceras både med x och med 3. Den distributiva lagen ger då (2x − 4) ∙ x + (2x − 4) ∙ 3. Med hjälp av den kommutativa lagen kan detta också skrivas x ∙ (2x − 4) + 3 ∙ (2x − 4), som i sin tur ger \( 2x^2 − 4x + 6x − 12 = 2x^2 + 2x − 12\).
Kvadreringsreglerna och konjugatregeln
För elever som behöver fler utmaningar inom algebra är ett ytterligare steg att arbeta med kvadreringsregeln och konjugatregeln och deras innebörd. Parallellt med att eleverna arbetar med att multiplicera binom kan de konstatera att produkten \( (a + b)(a – b) = a^2 – ab + ab – b^2 = a^2 – b^2\). Ett sätt att hålla konjugatregeln levande är att koppla den till huvudräkning. Multiplikationen 42 ∙ 38 kan skrivas om som (40 + 2)(40 − 2), vilket enligt konjugatregeln är lika med \(40^2-2^2\) eller 1 596. På motsvarande sätt kan man beräkna 73 ∙ 67 i huvudet som \((70 + 3)(70 − 3) = 70^2 − 3^2 = 4 891\).
I nästa steg bör eleverna även kunna gå bakvägen och faktoruppdela uttryck som \(4x^2 − 3^2 i (2x + 3)(2x − 3)\).
Därmed kan eleven lösa andragradsekvationer som \(4x^2 − 9 = 0\) genom att skriva om dem som (2x + 3)(2x − 3) = 0 vilket ger de två rötterna x = 1,5 och x = −1,5.
Kvadreringsreglera behandlas på motsvarande sätt:
\((a + b)^2 = (a + b)(a + b) = a^2 + ab +ab + b^2 = a^2 + 2ab + b^2\) och
\((a − b)^2 = (a − b)(a − b) = a^2 − ab − ab + b^2 = a^2 − 2ab + b^2.\)
Uppmärksamma eleverna på strukturen. De ska inte behöva räkna ut \((2x + 3)^2\) steg för steg utan direkt se att termerna är \((2x)^2 + 2 ∙ 2x ∙ 3 + 3^2 = 4x^2 + 12x + 9\). Ännu viktigare är det att kunna gå bakvägen och känna igen att \(x^2 − 4x + 4 = (x − 2)^2\) och att \(x^2 + 6x + 9 = (x + 3)^2\).
Ekvationer. TAe
Delområdet TAe omfattar följande fem diagnoser.
TAe1
Enkla ekvationer
TAe2
Ekvationer
TAe3
Ekvationer, rationella tal
TAe4
Ekvationer med och utan lösning
TAe5
Olikheter
TAe6
Andragradsekvationer
TAe7
Ekvationssystem, algebraisk lösning
Arbetet med de här diagnoserna förutsätter att eleverna har förkunskaper från delområdet Grundläggande aritmetik, AG.
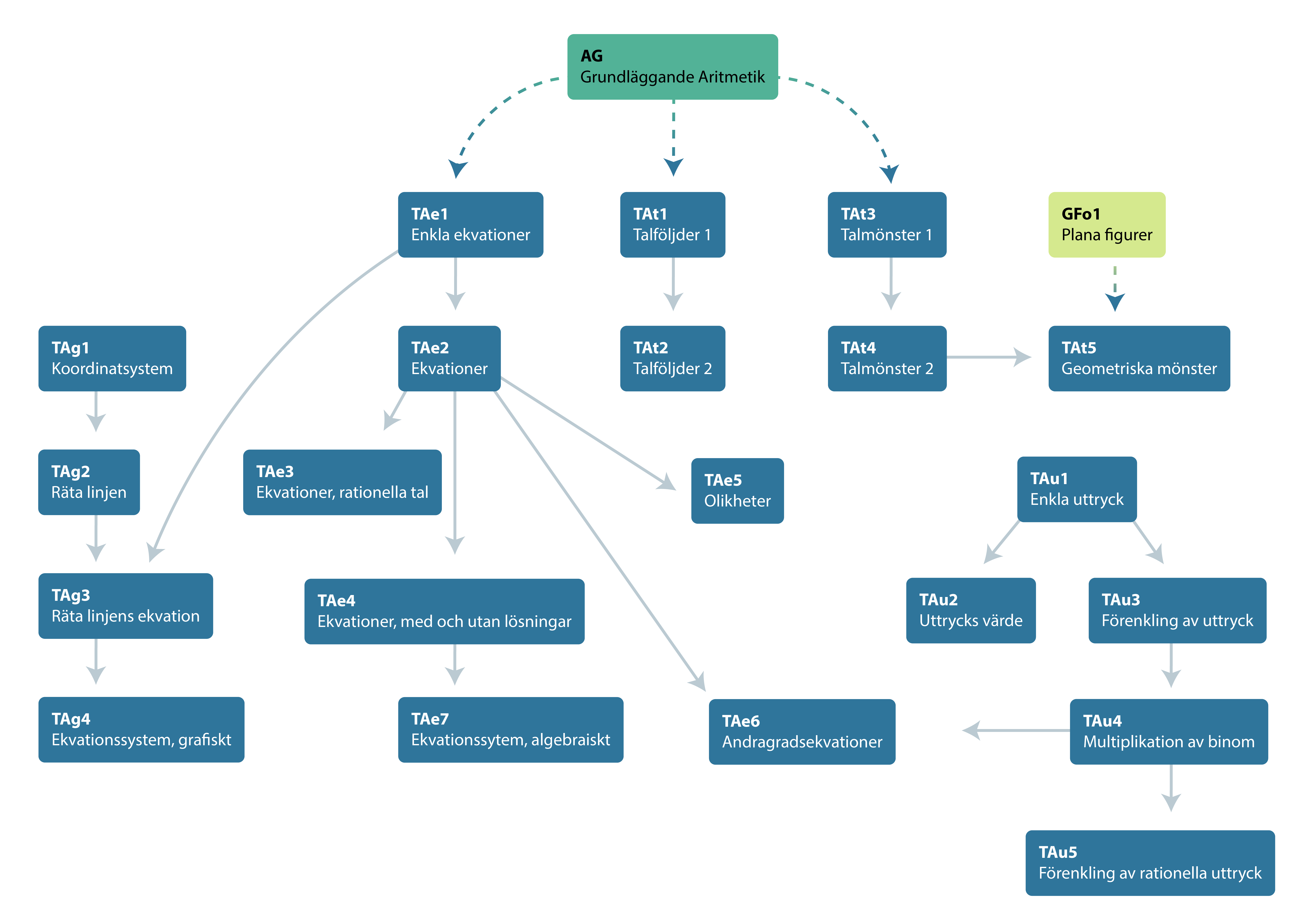
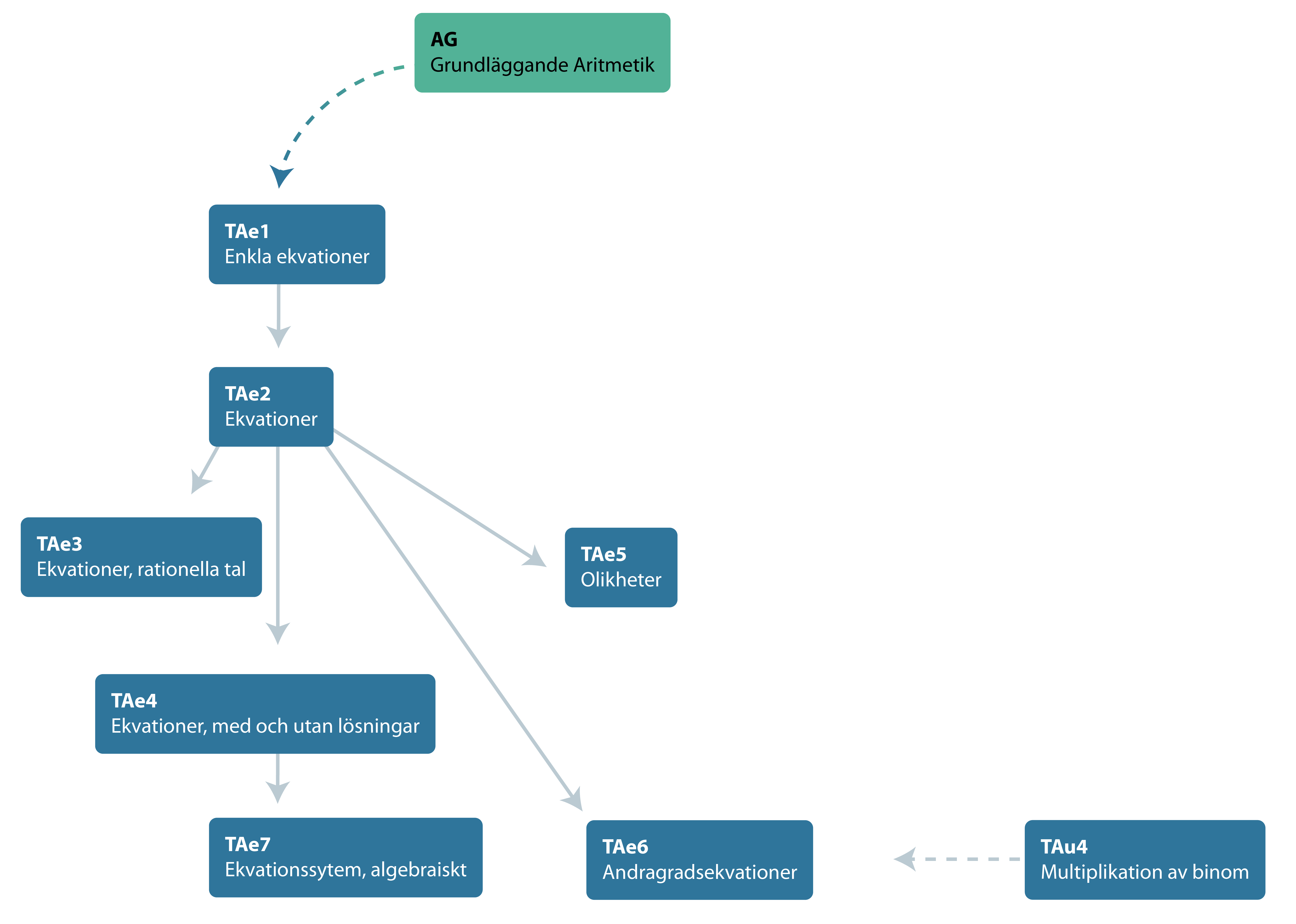
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Där framgår att TAe1 är förkunskap till TAe2, som i sin tur är förkunskap till TAe3, TAe4, TAe5 och TAe6. TAe4 utgör förkunskap till TAe7. Vidare kräver TAe6 förkunskaper frånTAu4, Multiplikation av binom. Självklart finns det också ett samband med de första diagnoserna inom delområde TAu där man testar elevens förståelse av enkla uttryck, uttrycks värden och förenkling av uttryck. Dessa samband är dock inte utritade i strukturschemat.
Didaktiska kommentarer till delområdet TAe
Målet är att eleverna ska kunna formulera en ekvation utifrån en problemlösningssituation, lösa ekvationen och sedan tolka resultatet i förhållande till det ursprungliga problemet. Detta innebär att eleven måste kunna uppfatta problemets struktur och uttrycka det algebraiskt samt kunna bearbeta uttrycket och lösa ekvationen. I detta delområde testas elevens förmåga att lösa ekvationer.
En ekvation är avkontextualiserad och eleverna måste kunna hantera symbolerna i sig men för att kunna använda ekvationer som redskap vid problemlösning räcker det inte att de mekaniskt kan hantera symbolerna. God taluppfattning och kännedom om räkneregler och räknelagar krävs.
Ekvationerna kan till att börja med lösas informellt med hjälp av matematiska resonemang eller genom att först göra en uppskattning (gissning) och sedan pröva.
Eleverna bör därefter utöka sin förmåga att lösa enkla ekvationer i situationer som är relevanta för eleven. Det handlar om ekvationer av typen 5x − 10 = 2x + 2 som bör lösas formellt korrekt med hjälp av annulleringslagarna. Metoderna ska nämligen senare kunna generaliseras till mer komplicerade ekvationer. En lösning av en ekvation ska alltid avslutas med en kontroll av att lösningen satisfierar ekvationen.
Annulleringslagen för addition innebär att samma tal kan adderas (eller subtraheras) på båda sidor om likhetstecknet utan att förändra sanningshalten i ekvationen. Annulleringslagen för multiplikation innebär att samma tal (bortsett från 0) kan multipliceras (eller divideras) på båda sidor om likhetstecknet utan att förändra sanningshalten i ekvationen.
Även ekvationer som 4x − 7 = 4x och 2x − 2 = 4x − 2 + 2x bör diskuteras. I det första fallet ger annulleringslagarna 0 = 7, vilket är en falsk utsaga. Den ekvationen saknar därför lösningar. I det andra fallet kan ekvationen skrivas 2x − 2 = 2x − 2 eller som 0 = 0. Detta är en sann utsaga oberoende av x. Det betyder att ekvationen har oändligt många lösningar. Med hjälp av ekvationsspelet är det lätt att konkretisera reglerna för ekvationslösning, även för betydligt yngre elever.
Även uppgifter med x i nämnaren såsom 5/x + 4 = 2/x + 7 kan förekomma. Den här typen av uppgifter ger mycket att resonera om och övar förmågan att föra och följa matematiska resonemang. Tanken är i det här fallet att man inte behöver operera med x i nämnaren utan enbart med talet 1/x som om det vore ett naturligt tal. Med hjälp av annuleringslagen finner man att 1/x = 1 det vill säga att x = 1 Byter man ut 1/x mot y blir det ännu enklare.
Eleverna bör nu även möta ekvationer som 4 + 3x = 1 som har ett negativt tal (x = −1) som lösning och ekvationer som 4x − 1 = x + 1 vars lösning är ett tal i bråkform (x = 2/3). Vänj eleverna vid att alltid kontrollera att lösningen på en ekvation verkligen satisfierar (löser) ekvationen.
En elev som förstår ekvationslösningens idé, kan även lösa enkla ekvationer av andra graden. En ekvation som x(x − 1) = 0 är t.ex. enkel. För att vänster led ska bli lika med 0 måste ju minst en av faktorerna vara lika med 0. Det betyder att x = 0 och (x − 1) = 0 (alltså x = 1) löser ekvationen. Eleverna bör även kunna gissa sig till att ekvationen \(x^2 − 2x + 1 = 0\) har en lösning x = 1, eftersom x = 1 satisfierar ekvationen. Diskussioner av det här slaget avdramatiserar andragradsekvationen. Det här handlar om att använda matematikens uttrycksformer och att reflektera över och värdera valda strategier.
Nästa steg är att formellt kunna lösa ekvationssystem av andra graden. Innebörden i ett ekvationssystem är att man söker värden på x och y som satisfierar båda ekvationerna.
Det finns två metoder för att lösa ett sådant ekvationssystem algebraiskt. Den ena metoden kallas för insättningsmetoden den andra metoden kallas för additionsmetoden.
Det här handlar om matematiska begrepp och metoder och om matematikens uttrycksformer.
Ett alternativ till en algebraisk lösningsmetod är den grafiska metoden som behandlas i delområdet TAg.
Koordinatsystem och grafer. TAg
Delområdet TAg omfattar följande fyra diagnoser.
TAg1
Koordinatsystem
TAg2
Räta linjen
TAg3
Räta linjens ekvation
TAg4
Ekvationssystem grafisk lösning
Arbetet med de här diagnoserna förutsätter att eleverna har arbetat med koordinatsystem.
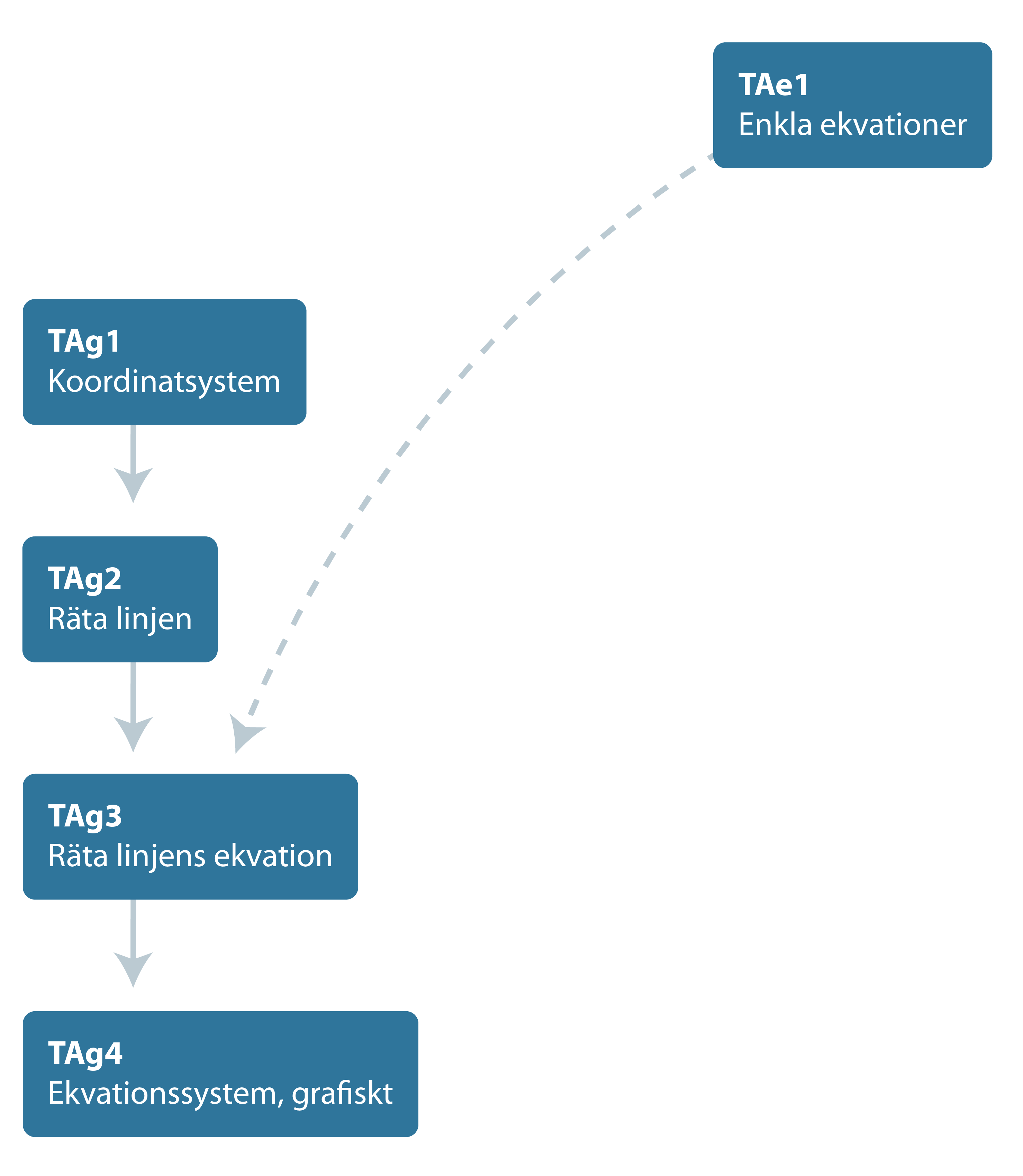
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Där framgår att TAg1, koordinatsystem, är förkunskap till räta linjen,TAg2, som i sin tur är förkunskap till TAg3, räta linjens ekvationer. TAg3 kräver som framgår av strukturschemat att även TAe1, enkla ekvationer, som förkunskap. Självklart finns det också ett samband med de första diagnoserna inom delområde TAe där man testar elevens förståelse av enkla (linjära) ekvationer. Dessa samband är dock inte utritade i strukturschemat.
Didaktiska kommentarer till delområdet TAg
Innehållet i delområdet bygger på att eleven förstår hur ett koordinatsystem är uppbyggt. Det inleds därför med en diagnos, där eleven ska avläsa punkter som till exempel (4, 3), (0, 4) och (6, 0) samt kunna rita in givna talpar som punkter i koordinatsystemet.
Koordinatsystemet är ett vanligt instrument inom matematiken för att kommunicera matematik. Man bör därför noga diskutera koordinataxlarnas gradering och hur man läser av och skriver koordinater, med x-koordinaten före y-koordinaten. Denna kompetens kommer även till uttryck när elever arbetar med exempelvis linjediagram (se diagnoser inom området S).
Den linjära funktionen är en av de vanligaste funktionerna vi möter i vardagen och den visar ett samband av typen y = kx + m. En speciell linjär funktion är proportionaliteten (detta behandlas i delområde RP, proportionalitet och procent). Exempel på proportionaliteter är kilopris och hastighet. Om kilopriset är k kr/kg så kan priset (y kr) för x kg tecknas y = k ∙ x. Detta svarar mot en enkel graf i form av en rät linje i ett koordinatsystem. En rät linje definieras av två punkter på linjen.
I samband med räkningar för el och telefoni, som består av en fast och en rörlig del kan undervisning kopplas till vardagssituationer. Om exemplet handlar om elräkning och den fasta delen är 1200 kr per år, den rörliga delen 2 kr per kWh och förbrukningen av el under ett år är x kWh, så blir priset y = 1 200 + 2x kr.
Anledningen till att funktioner som y = 1200 + 2x kallas linjära beror på att grafen är en rät linje. Undervisningen om detta kan inledas med att eleverna plottar grafen till funktionen i ett koordinatsystem och därefter konstaterar att grafen är en rät linje som skär y-axeln i punkten (0, 1200). Man konstaterar samtidigt att proportionaliteten också är en rät linje med tillägget den alltid går genom origo.
I nästa steg analyseras grafen till en linjär funktion som y = kx + m lite närmare. Det kan inledas med att man konstaterar att x = 0 ger y = m. Det innebär att grafen till funktionen y = kx + m, går genom punkten (0, m) på y-axeln. När variabeln x ökar med 1, så ökar variabeln y med k. Det innebär att grafen till y = 2x − 3 som går genom punkten (0, −3), också går genom punkterna (1, −1) och (2, 1). Koefficienten beskriver således grafens (linjens) lutning. När man vet detta behöver man inte plotta grafen till en linjär funktion, utan kan direkt rita grafen utgående från konstanterna k och m, där m alltså är linjens skärning med y-axeln och k är linjens lutning (riktningskoefficient).
Ekvationssystem av första graden, grafisk lösning
För att lösa ett ekvationssystem grafiskt ritar man graferna till de båda linjerna i ett koordinatsystem. Linjerna skär varandra i punkten (1, 2) som är lösningen till ekvationssystemet. Gör eleverna uppmärksamma på vad detta handlar om, nämligen att punkten (1, 2) ligger på båda linjerna och alltså satisfierar båda ekvationerna. Det här handlar om ett alternativt val av matematisk strategi och ett alternativt val av metod och modell.
Ett ekvationssystem kan även lösas algebraiskt. Detta behandlas i delområde TAe.