Sannolikhet och statistik. S
Sannolikhet och statistik. S
Sannolikhet och statistik. S
Området består av två delar sannolikhet och statistik. Diagnoserna i delområdet sannolikhet avser att kartlägga elevernas förmåga att arbeta med enkel kombinatorik, att använda träddiagram samt att beräkna sannolikhet i olika situationer.
Diagnoserna i delområdet statistik avser att kartlägga om eleverna kan ordna, avläsa, tolka och presentera statistiska data i tabeller och diagram, samt bestämma enkla lägesmått.
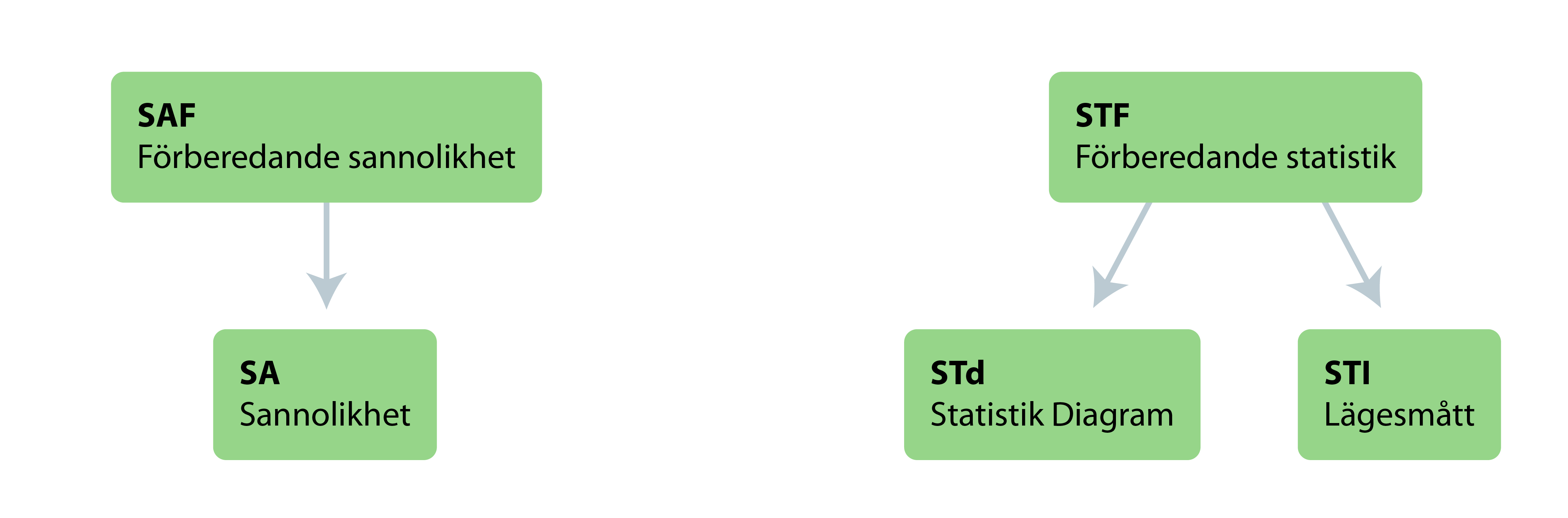
Området består av följande fem delområden inom Sannolikhet och Statistik.
SAF
Förberedande sannolikhet
SA
Sannolikhet
STF
Förberedande statistik
STD
Statistik Diagram
STl
Lägesmått
Strukturschemat visar att det inte finns några direkta kopplingar mellan sannolikhet och statistik. Det betyder att innehållet inom dessa områden kan behandlas i valfri ordning eller parallellt. Det finns en naturlig koppling mellan områdena på så sätt att det var utvecklingen av sannolikhetslära som vetenskap som gjorde det möjligt att utveckla statistiken genom att använda begränsade slumpmässiga urval som grund för att dra slutsatser ur statistiskt material. Statistikområdet innhåller diagnoser som på två olika sätt beskriver statistiskt material. Dels tabeller och diagram, dels lägesmått.
Detta är två uttryckssätt som till stora delar kompletterar varandra. De ingår därför i samma delområde.
Diagnosområdet i relation till syfte och centralt innehåll i kursplanen i matematik
Med hjälp av diagnoserna inom detta område kan man ta reda på om elever har byggt upp ett begreppsförråd och ett verktygsförråd inom sannolikhet och statistik som behövs för att utveckla förmågan att:
- formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder,
- använda och analysera matematiska begrepp och samband mellan begrepp,
- välja och använda lämpliga matematiska metoder för att göra beräkningar och lösa rutinuppgifter
- föra och följa matematiska resonemang, och
- använda matematikens uttrycksformer för att samtala om, argumentera och redogöra för frågeställningar, beräkningar och slutsatser
Inom området ges det stora möjligheter för eleven att använda matematikens uttrycksformer.
Det är viktigt att eleverna får möta innehållet genom upplevda och verklighetsförankrade situationer som man gemensamt resonerar om för att på så sätt skapa förståelse för begrepp och metoder. Detta ger i sin tur eleven möjlighet att välja och värdera lämpliga metoder samt att kunna lösa uppgifter, såväl rutinuppgifter som problemlösningsuppgifter.
Diagnoserna ger eleven möjlighet att visa kunskaper inom följande centrala innehåll:
Årskurs 1–3
Sannolikhet och statistik:
- Slumpmässiga händelser i experiment och spel
- Enkla tabeller och diagram och hur de kan användas för att sortera data och beskriva resultat från enkla undersökningar.
I kunskapskrav för godtagbara kunskaper i årskurs 3 finns följande: Eleven kan vid olika slag av undersökningar i välkända situationer avläsa och skapa enkla tabeller och diagram för att sortera och redovisa resultat. Eleven ska alltså såväl passivt kunna tolka diagram som aktivt själv skapa diagram. Vidare ska eleven kunna föra och följa matematiska resonemang vilket kräver förståelse av begrepp inom området.
Årskurs 4–6
Sannolikhet och statistik:
- Sannolikhet, chans och risk grundat på observationer, experiment eller statistiskt material från vardagliga situationer. Jämförelse av sannolikheten vid olika slumpmässiga försök.
- Tabeller och diagram för att beskriva resultat från undersökningar. Tolkning av data i tabeller och diagram.
- Lägesmåtten medelvärde, typvärde och median samt hur de kan användas i statistiska undersökningar.
I kunskapskraven i slutet av årskurs 6 framkommer att eleven ska förstå begrepp som hör till området samt kunna använda dem och välja lämpliga matematiska metoder och uttrycksformer för beräkningar och resonemang på olika nivåer och i olika situationer inom sannolikhet och statistik.
Årskurs 7–9
Sannolikhet och statistik:
- Likformig sannolikhet och metoder för att beräkna sannolikheten i vardagliga situationer.
- Hur kombinatoriska principer kan användas i enkla vardagliga och matematiska problem.
- Tabeller, diagram och grafer samt hur de kan tolkas och användas för att beskriva resultat av egna och andras undersökningar, till exempel med hjälp av digitala verktyg. Hur lägesmått //…// kan användas för bedömning av resultat vid statistiska undersökningar.
- Bedömningar av risker och chanser utifrån statistiskt material.
I kunskapskraven i slutet av årskurs 9 framkommer att eleven ska ha förståelse för matematiska begrepp som hör till området samt kunna använda dem och välja lämpliga matematiska metoder och uttrycksformer för beräkningar och resonemang på olika nivåer och i olika situationer inom sannolikhet och statistik.
Didaktiska kommentarer till område S
Sannolikhetslära används inom många olika vetenskaper. Det är till exempel sannolikhetsberäkningar som ligger till grund för hur man kan dra slutsatser ur statistiskt material, vilket i sin tur kan användas för att räkna ut risk och möjlighet att olika händelser ska inträffa. Till vardags dyker sannolikhet upp i till exempel spelsituationer och vid lottdragning.
Slumpbegreppet kan vara svårt för elever att hantera eftersom det kan strida mot den intuitiva uppfattningen. Inte sällan styrs elever av psykologiska förklaringar i sina slutsatser. Som exempel kan en del elever tro att det är lättare att få en viss sida upp på tärningen för att det är deras ”lyckotal” eller att det är lättare att få en sexa i ett kast om de inte har fått en sexa i flera tidigare kast. Att få en sexa skulle därför vara ”rättvist”.
De beräkningar som utförs inom sannolikhetsläran resulterar ofta i relativt stora tal eftersom antalet kombinationer snabbt blir många. Det gäller därför att börja med försök där antal möjliga utfall är begränsade och där man kan åskådliggöra situationen med enkla tabeller eller träddiagram. Ur träddiagrammen bör man så småningom kunna dra generella slutsatser om principer för sannolikhetsberäkningar för att senare även kunna räkna på situationer där ett större antal möjliga utfall och upprepade händelser ingår.
Inom statistiken ges möjlighet att uttrycka och beskriva verkliga situationer med hjälp av matematikens uttrycksformer. Elever ska kunna avläsa och konstruera olika slags diagram, kunna välja lämpligt diagram för olika undersökningar, kunna tolka, dra slutsatser och argumentera utifrån statistisk information, samt kunna beräkna och tillämpa lägesmått.
Statistik är ett matematiskt innehåll som på ett naturligt sätt kan användas vid till exempel tematiskt arbete inom olika ämnesområden där det krävs slutsatser som bygger på användning av statistik. Detta kan vara ett sätt att motivera elever till att arbeta med statistisk. Det kan även vara lämpligt att knyta statistik till vardagen genom använda sig av dagstidningar och annan aktuell information i undervisningen.
Eleverna bör även få konstruera diagram med hjälp av tekniska hjälpmedel vilket dels ger snygga och läsbara diagram, dels ger eleverna en inblick i användandet av tekniska hjälpmedel. Det gäller då att ha en dialog med eleverna för att säkerställa att de förstår innebörden av vad som visas på skärmen.
Sannolikhet och statistik. Alla diagnoser
Sannolikhet. SA
Delområdet SA består av följande sex diagnoser:
SAF
Förebredande, sannolikhet
SA1
Grundläggande kombinatorik
SA2
Kombinatorik
SA3
Grundläggande sannolikhet
SA4
Experimentell sannolikhet
SA5
Sannolikhet
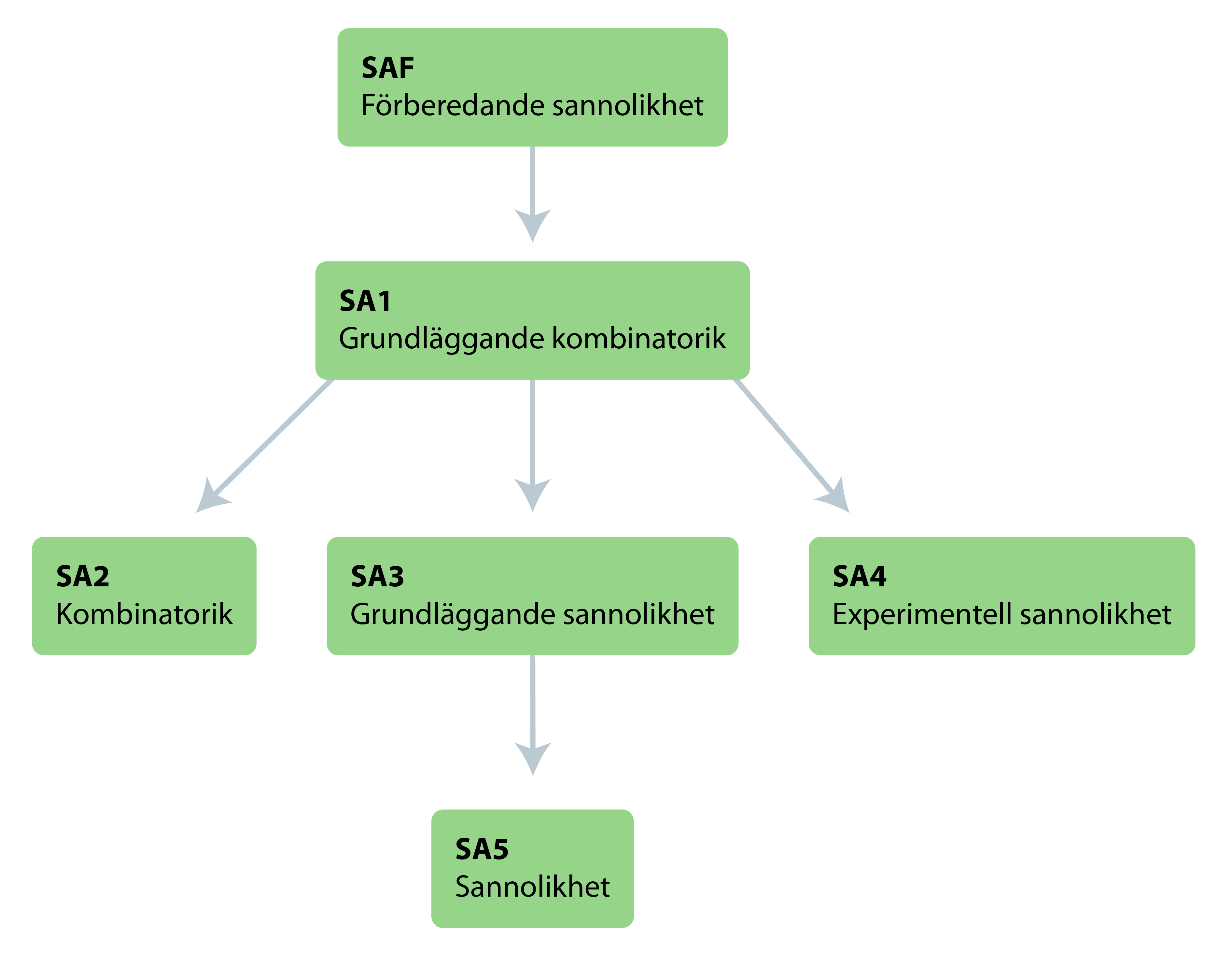
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan.
SAF behandlar elevens grundläggande förmåga att resonera och dra logiska slutsatser om rimlighet i förhållande till observationer och erfarenheter och utgör därmed förkunskaper till följande diagnoser. Diagnoserna SA1, som behandlar antal möjliga kombinationer, utfall, utgör grunden för senare sannolikhetsberäkningar diagnos SA3, SA3 och SA4.
Didaktiska kommentarer till delområdet SA
Sannolikhet är ett mått på hur troligt det är att en viss händelse inträffar. Sannolikheten för en viss händelse beräknas som kvoten mellan antal gynnsamma möjligheter (utfall) och totala antalet möjligheter (utfall).
För att ta reda på hur stort antal möjliga utfall samt antal gynnsamma utfall är används principer för kombinatorik.
För att hitta alla möjliga utfall behöver man gå systematiskt tillväga och bokföra på ett överskådligt sätt. Redan vid ett begränsat antal valmöjligheter kan totala antalet kombinationer bli stort. Att rita träddiagram är en strategi för att gå systematiskt tillväga och få en överblick över både möjliga och gynnsamma utfall. Träddiagram fungerar bra om antalet utfall inte är alltför stort.
Med hjälp av träddiagram kan man senare få förståelse för multiplikationsprincipen. Multiplikationsprincipen säger att sannolikheten för att en följd av händelser ska inträffa tas fram genom att man multiplicerar sannolikheterna för att samtliga önskvärda ingående händelse ska inträffa. (En följd av händelser kan till exempel vara att först få en trea och sedan en fyra om man kastar en tärning två gånger).
Även additionsprincipen kan inses med hjälp av uppritade träddiagram. Additionsprincipen anger att sannolikheten för en händelse där flera olika alternativ är gynnsamma, beräknas som summan av sannolikheterna för alla dessa olika alternativa händelser. (En händelse där flera olika alternativ är gynnsamma är till exempel möjligheten att få minst en trea vid kast med en tärning. Då är alla de fyra utfallen trea, fyra, femma eller sexa, samtliga gynnsamma).
Elever bör få närma sig kombinatorik och sannolikhetslära genom experiment och laborationer där sannolikhet för olika utfall tas fram på experimentell väg och systematiskt bokförs. Resultaten bör sedan diskuteras och ligga till grund för mer generella slutsatser. Denna grundläggande förståelse kan under senare skolår utvecklas med matematiska uttryck för beräkning av sannolikheter i mer komplexa situationer.
Det kan vara lämpligt att börja arbeta med likformiga (symmetriska) utfallsrum, där varje utfall har lika stor möjlighet att inträffa, exempelvis kast med tärning. Sedan kan man gå vidare till händelser med olikformiga sannolikheter för olika utfall.
Ett annat sätt att ge progression i arbetet är att börja med enstaka händelser för att sedan även arbeta med situationer där ett antal händelser sker i följd. Ett exempel är tre kast i rad med en tärning eller ett antal dragningar av kulor ur en burk, både med och utan återläggning. Förståelse för språkliga begrepp får en central betydelse, till exempel att vid kast med tärning få minst tre, högst tre, åtminstone tre, exakt tre, allt utom tre.
Statistik. ST
Delområdet ST består av nio diagnoser grupperade i två delar diagram och lägesmått:
STF
Förebredande statistik
STd1
Tabeller
STd2
Stapeldiagram
STd3
Stolpdiagram
STd4
Cirkeldiagram
STd5
Linjediagram
STd6
Histogram
STl1
Grundläggande lägesmått
STI2
Lägesmått
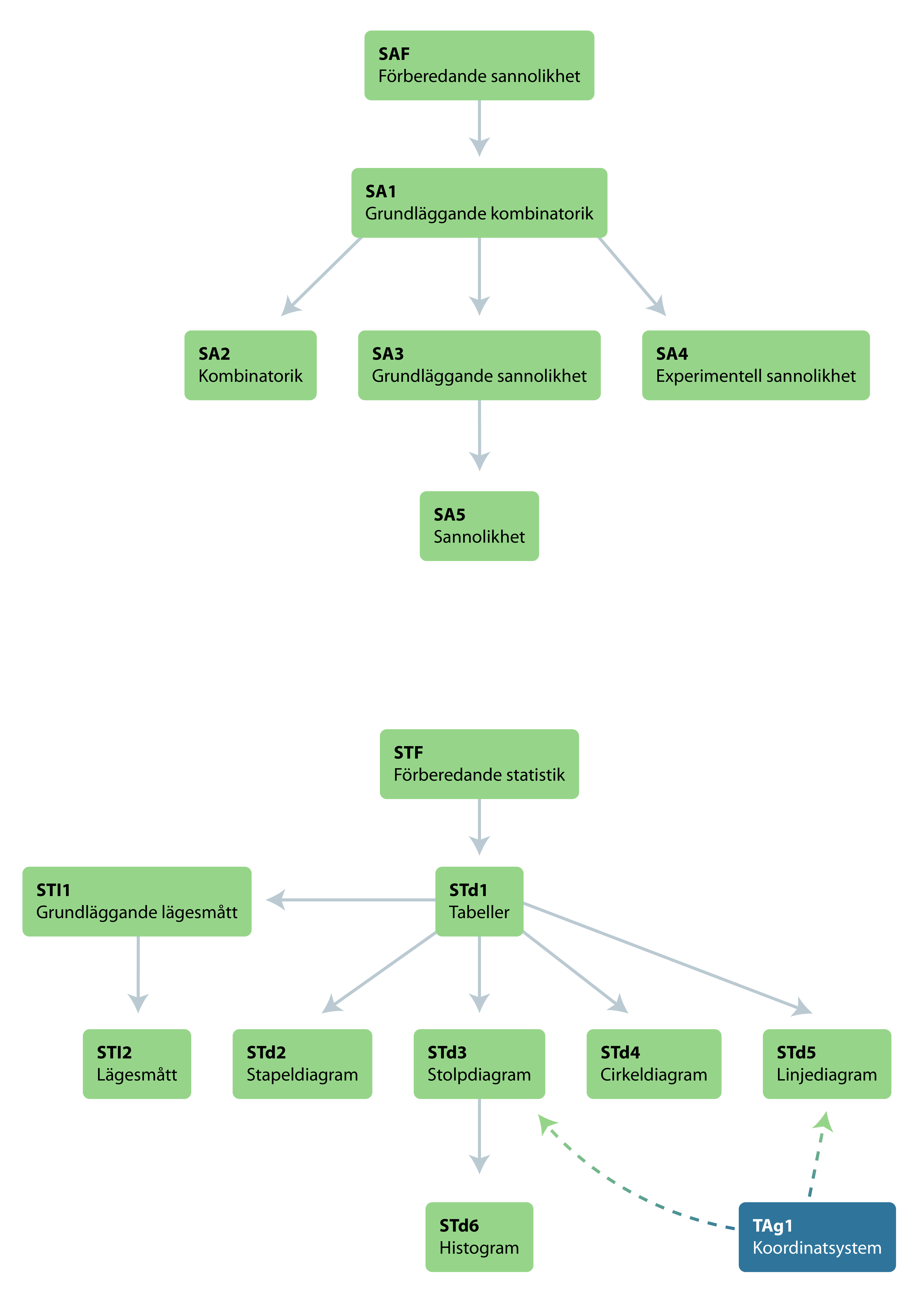
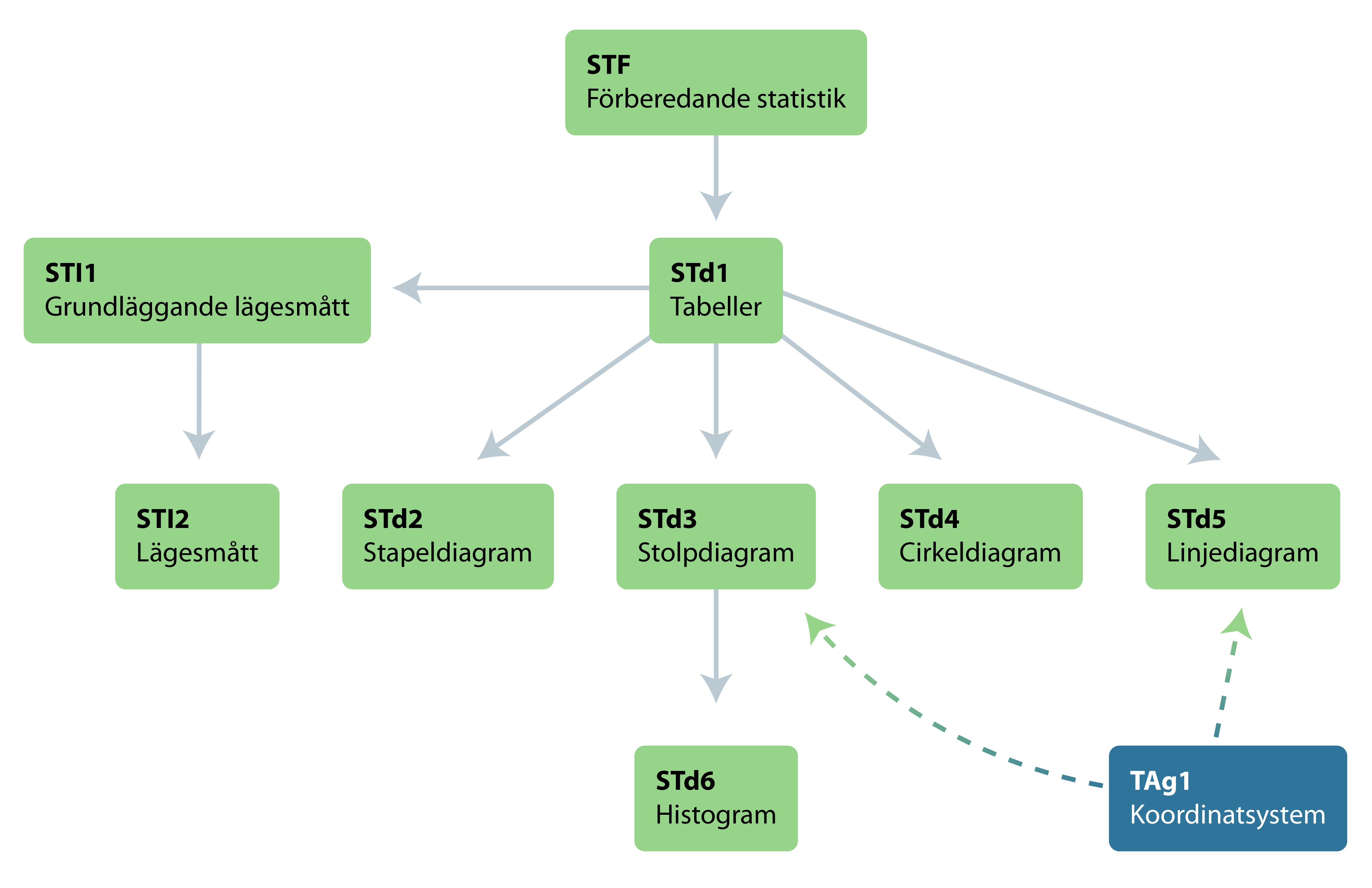
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan.
Grunden för statistik är sortering och klassificering av material vilket behandlas informellt i STF samt mer formellt, i form av tabeller, i STd1. Sedan följer de olika diagramtyperna för presentation av statistiskt material. Detta testas med diagnoserna STd2–STd6. Parallellt kan man arbeta med olika typer av lägesmått och för det innehållet finns diagnoserna STl1–STl2.
Didaktiska kommentarer till delområdet ST
En förutsättning för att kunna förstå uppbyggnaden av tabeller och diagram är att eleven kan sortera och klassificera data utgående från olika principer. Dessa data kan sedan organiseras och presenteras på olika sätt.
En metod att beskriva data är att använda sig av tabeller och diagram. Eleverna behöver därför kunna: överföra enkla rådata till tabeller och omvänt kunna avläsa data i tabeller av olika slag.
Ibland kan det vara enklare att få en överblick över ett material om det presenteras i form av ett diagram. Eleverna bör därför kunna: tolka diagram såsom stapeldiagram, stolpdiagram, cirkeldiagram, linjediagram och histogram.
För att på djupet förstå hur ett diagram är uppbyggt är det dessutom viktigt att eleverna kan överföra enkla data till diagram av olika typer.
En annan metod att beskriva data är att använda sig av lägesmått (och spridningsmått). Eleven ska därför kunna bestämma enkla lägesmått och utgående från dem bilda sig en uppfattning om beskrivna data.
Tabeller och diagram innehåller ofta en hel del information. För att denna information ska kunna tolkas på ett korrekt sätt, finns det ett antal enkla regler för hur tabeller och diagram ska byggas upp. Det är viktigt att dessa regler introduceras och följs även under de första årskurserna.
För att kunna arbeta med statistiska data krävs en god taluppfattning eftersom det till stor del handlar om att avläsa, ordna och jämföra tal. För att bestämma ett aritmetiskt medelvärde krävs det dessutom att eleven kan addera ett antal tal och därefter utföra en division. Eftersom syftet med de här diagnoserna är att kartlägga elevernas förmåga att hantera idéerna för att handskas med statistiska data, har den aritmetiska färdigheten i uppgifterna tonats ned. Eleverna ska inte behöva göra fel på uppgifterna av aritmetiska skäl. Utgångspunkten är att elever kan, eller lätt kan, lära sig att kombinera kunskaper. Behärskar därför en elev de statistiska idéerna med enklare tal och räkneoperationer, kan dessa idéer även användas med svårare tal och räkneoperationer.
Diagnoserna inom det här delområdet omfattar uppgifter av stegrad svårighetsgrad. Det betyder att elever i de tidigare årskurserna troligen inte kan lösa alla uppgifter på en diagnos. Man kan då antingen välja ut lämpliga uppgifter på diagnosen, eller tala om för eleverna att vissa uppgifter kanske är för svåra, men uppmana dem att försöka lösa så många uppgifter som möjligt.
Diagnoserna som ingår i området bör emellertid betraktas som helheter, vilka var för sig ger en viss typ av information. Om man ger delar av en diagnos är det därför viktigt att studera vad de olika uppgifterna mäter. Risken är annars att man tappar någon viktig aspekt.
Det är viktigt att eleverna lär sig skilja mellan olika typer av diagram och i vilka situationer man använder de olika diagrammen. Det är också viktigt att man diskuterar användningen av typvärde, median och medelvärde samt att eleverna lär sig att tolka innebörden av låddiagram, gärna kopplat till situationer från vardagen eller till andra ämnen.