Aritmetik. A
Aritmetik. A
Aritmetik. A
AF
Förberedande aritmetik
AG
Grundläggande aritmetik
AS
Skriftlig räkning
AU
Utvidgad aritmetik
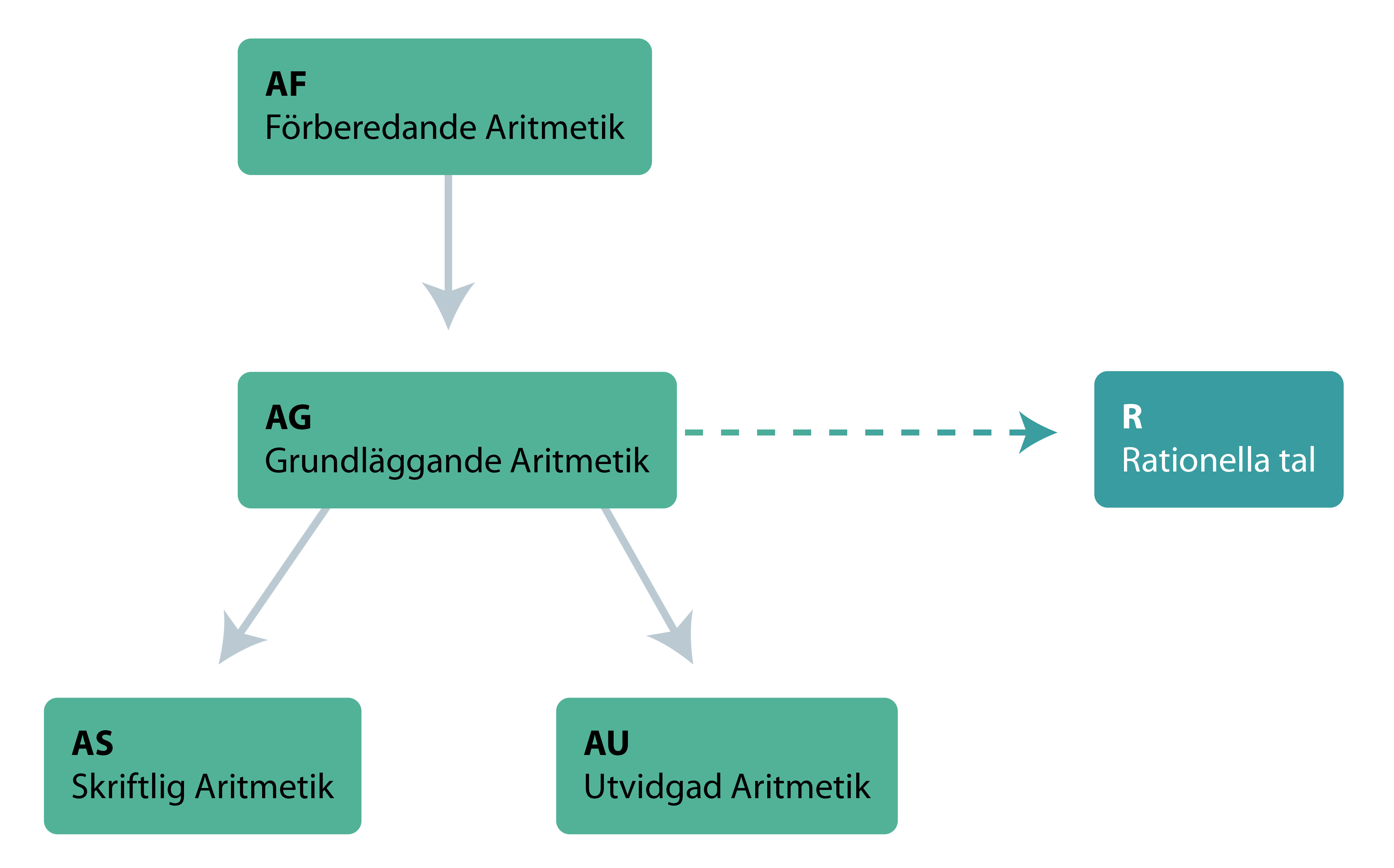
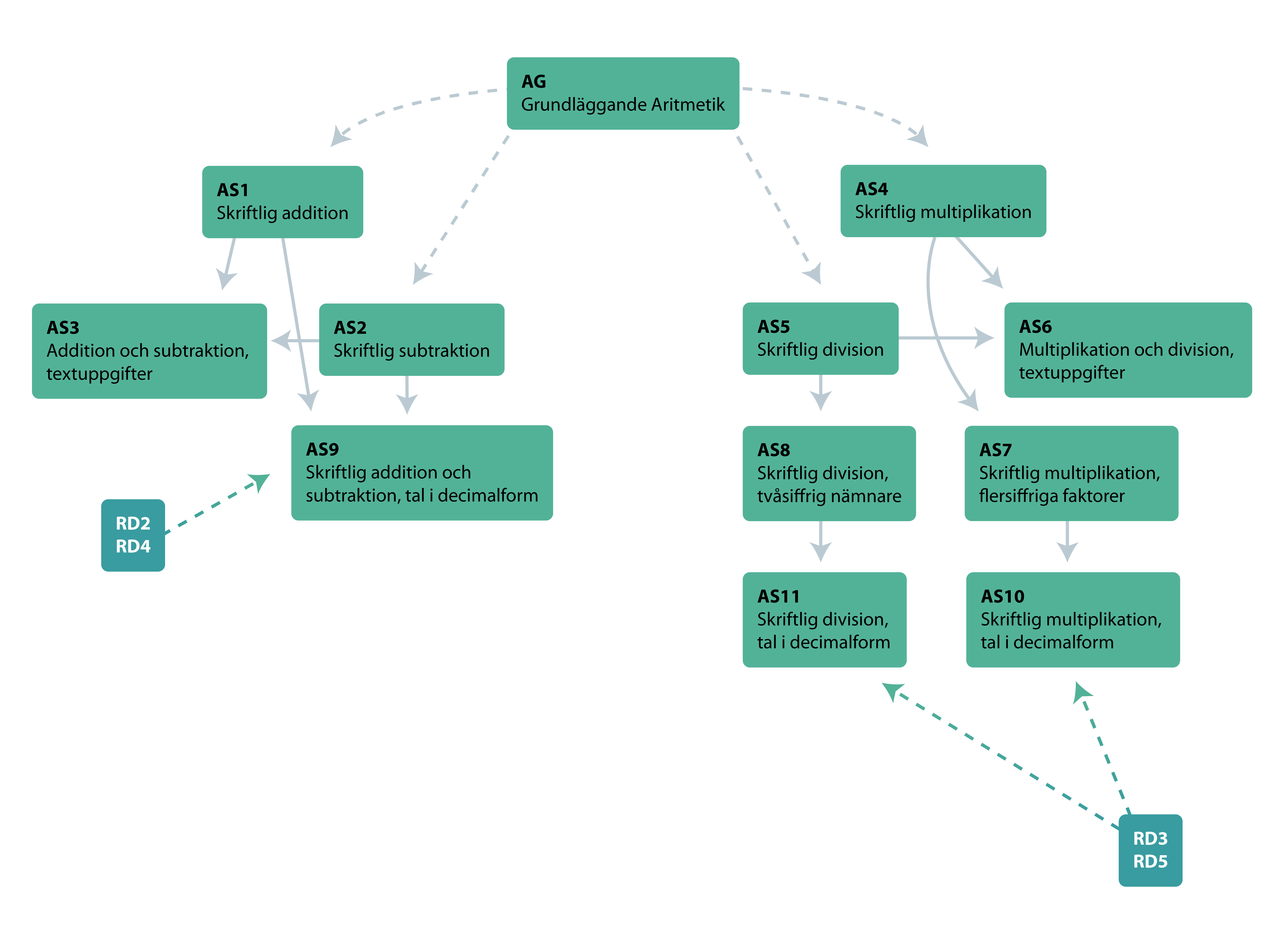
Sambandet mellan delområdena ser ut så här:
Strukturschemat visar att förberedande aritmetik, AF är förkunskaper till grundläggande aritmetik, AG, som i sin tur innehåller förkunskaper till skriftlig räkning, AS och utvidgad aritmetik, AU. AG är även förkunskap till R som handlar om de rationella talen och dess aritmetik.
Didaktiska kommentarer till område A
Om räknelagar och räkneregler
Den grundläggande aritmetiken har en avgörande betydelse för elevens fortsatta matematikinlärning. Matematikkunskaper handlar inte enbart om att kunna räkna, utan om att förstå den matematik som används. Redan i årskurs 1 bör eleverna få kännedom om de grundläggande begrepp som utgör basen för
all matematik. Alla dessa begrepp kan konkretiseras i undervisningen. Målet med konkretiseringen är att den ska leda till abstraktion. Ju tidigare en elev tillägnar
sig dessa grundläggande begrepp desto lättare blir det för eleven att såväl lära sig mer matematik, som att utveckla intresse för matematik och tilltro till sin förmåga att använda matematik i olika sammanhang.
Under de första skolåren är det viktigt att eleverna utvecklar en bra taluppfattning och att de får ett bra flyt i räknandet. En förutsättning för detta är att man talar matematik med eleverna och att de får öva på ett meningsfullt och utvecklande sätt. Eleverna bör också göras medvetna om att undervisningen inte går ut på att enbart göra saker inom matematik utan att förstå vad de gör, t.ex. att kunna utföra beräkningar på ett sätt som senare kan generaliseras till nya områden. Följande aspekter av en taluppfattning bör eleven möta under de första skolåren, med början redan i förskolan och förskoleklassen.
Taluppfattning handlar om att ha en sådan känsla för hur talen är uppbyggda, att man direkt, utan att reflektera, kan operera med talen. I en sådan taluppfattning ingår
att behärska behärska talens ordning och dess grannar såsom:
- att 6 + 1 = 7 eftersom 7 är talet efter 6
- att 8 – 1 = 7 eftersom 7 är talet före 8
- att 8 – 7 = 1 eftersom talen 7 och 8 är grannar
att behärska positionssystemet med basen 10 samt 10 tals- och 100 tals-övergångar såsom:
- att 18 betyder 10 + 8
- att 35 betyder 3 · 10 + 5
- att 98 + 3 = 101
- att 101 – 2 = 99
att kunna tillämpa de grundläggande räknelagarna, i första hand:
- de kommutativa räknelagarna: \(a + b = b + a\) och \(a \cdot b = b \cdot a\)
- de associativa räknelagarna \( (a + b) + c = a + (b + c) \) och \( (a \cdot b) \cdot c = a \cdot (b \cdot c) \)
- den distributiva lagen: \( a \cdot (b + c) = a \cdot b + a \cdot c \)
att behärska tals uppdelning i termer och faktorer såsom
- att 10 = 8 + 2 och 7 = 5 + 2, vilket i sin tur ger en förklaring till tiotalsövergången 8 + 7 = 8 + 2 + 5 = 10 + 5
- att 28 = 4 ∙ 7 och 100 = 4 ∙ 25, vilket kan utnyttjas vid beräkningar som 28 ∙ 25 = 7 ∙ 4 ∙ 25 = 7 ∙ 100 i huvudet
att behärska tals storleksordning, att avrunda tal och
- att arbeta med runda tal såsom
- att 32 – 19 är ungefär lika med 32 – 20, men 1 mer. (Det är som att köpa något för 19 kr, betala med två tior och få en krona tillbaka.)
- att genom lika tillägg (differens) se att 32 – 19 = 33 – 20, (Man kan t.ex. tänka på åldersskillnaden 32 år och 19 år, som är densamma om ett år.)
Elever bygger inte upp en grundläggande taluppfattning av sig själva. För detta krävs en genomtänkt, långsiktig planering från lärarens sida och rika tillfällen för eleven att praktisera kunskapen. Detta arbete bör grundläggas i årskurs 1 och därefter följas upp och fördjupas under hela skoltiden.
Det räcker emellertid inte med att ha en bra taluppfattning. En förutsättning för att elever ska kunna operera med tal, alltså att kunna utföra beräkningar, är att de behärskar talen och dess egenskaper på ett sådant sätt att operationerna kan ske med flyt. Det kan jämföras med läsinlärning. Det räcker inte med att förstå hur bokstäverna uttalas och hur de kan sammanfogas till ord. För att läsningen ska bli funktionell måste läsandet ske med flyt, alltså kunna utföras så automatiskt att eleverna kan fokusera på innehållet i det lästa och inte på avkodandet av bokstäver och morfem.
Diagnoserna inom området aritmetik testar om eleven har abstraherat det grundläggande aritmetikkunnandet. Dessa diagnoser ska ges först när man tror att eleven har abstraherat och behärskar detta kunnande. Diagnoserna ges på tid för att eleven ska få möjlighet att visa att hon har flyt i sitt kunnande.
Aritmetik. Alla diagnoser
Didaktiska kommentarer till delområdet AF
Vad ingår i en grundläggande
taluppfattning?
När eleverna börjar förskoleklassen/skolan har de mycket olika erfarenheter av matematik. Vissa av dem kan redan talens namn och ordning upp till 20 och kan dessutom räkna 10–20 föremål. Andra kan ännu inte detta. Såväl forskning som beprövad erfarenhet visar att elever i den senare gruppen riskerar att få svårigheter i sin matematiska utveckling.
Forskning visar att barn har en förmåga att förstå och lära grundläggande matematik i tidiga åldrar.
Två forskare som ägnat stor uppmärksamhet åt detta och som fortfarande utgör en central referens inom området, är Gelman och Galistel (1978). De menar att barns förmåga att hantera tal är i det närmaste genetiskt betingat och byggs upp på samma sätt som modersmålet. Det innebär att barn som har utvecklat sin förmåga att tala också borde kunna hantera grundläggande räkning. Den enda väsentliga skillnaden består
i att barn hela tiden omges av ett språk medan de inte alltid omges av motsvarande numeriska miljö. Som exempel vet man att barn som är döva blir sena i sin språkutveckling, men att detta inte beror på bristande språklig förmåga. På motsvarande sätt kan ett barn inte bygga upp en förmåga att räkna om det växer upp i en miljö där man inte räknar.
När elever lär sig läsa, bygger läsandet på att de har en erfarenhet av att tala. Samma sak gäller för matematik. I skolan börjar man tidigt med att läsa och skriva siffror. För de elever som ännu inte har upptäckt och lärt sig använda matematik i vardagen kan detta försvåra inlärningen. Av det skälet är det viktigt att tidigt kartlägga elevers grundläggande taluppfattning och därmed förebygga svårigheter som annars kan uppstå.
Genom bland andra Gelman och Galistels forskning kan man bilda sig en uppfattning om vad det innebär att kunna räkna föremål. De delar upp denna förmåga i fem delar, fem principer. De första tre av dessa är:
- Abstraktionsprincipen som innebär att det är möjligt att bestämma antalet föremål (element) i varje väl avgränsad mängd.
- Ett-till-ett principen som innebär att man, genom att ordna föremål parvis, kan avgöra om två mängder innehåller lika eller olika många föremål.
- Principen om godtycklig ordning som innebär att man får samma resultat oavsett i vilken ordning man räknar föremålen.
De här tre principerna anses vara genetiskt nedärvda och brukar utvecklas i tidig ålder. För att barn ska kunna hantera dem krävs det emellertid en miljö där principerna kan användas. De två övriga principerna utvecklas i en social kontext (sammanhang) och kräver träning. Dessa principer är:
- Principen om talens stabila ordning. För att kunna ange antalet föremål i en mängd krävs det att man gör en ett-till-ett tillordning (parbildning) mellan räkneord och föremål. Detta kräver att man behärskar talens namn i rätt ordning.
- Antalsprincipen som innebär att det sist nämnda talnamnet vid en uppräkning (enligt princip 4) anger antalet föremål i den uppräknade mängden.
Att ett barn får svårt med att hantera tal eller antal, beror i allmänhet på att barnet ifråga ännu inte har förstått en eller flera av de nämnda principerna. Denna grundläggande förståelse är nödvändigt för att kunna följa skolans undervisning i matematik.
En del av syftet med undervisningen i matematik är att eleven ska abstrahera, alltså lämna det konkretiserande arbetet och utföra matematiska operationer i huvudet. Det som diagnostiseras i uppgifterna 7 och 8 på diagnosen inom delområdet är om eleverna nått detta stadium i sin utveckling, att de på en enkel nivå har lämnat det konkretiserande arbetet. För de elever som ännu inte har abstraherat och därmed inte klarat dessa delar av diagnosen krävs ny inlärning. Denna inlärning bör utgå från en konkretisering med avsikten att eleven ska förstå idén, alltså att de har abstraherat. Detta innebär att dessa båda uppgifter ska lösas i huvudet, inte med hjälp av fingrar eller material.
Grundläggande aritmetik. AG
Delområdet AG omfattar följande nio diagnoser:
AG1
Additioner och subtraktioner inom 1–9
AG2
Additioner och subtraktioner inom 10–19, utan tiotalsövergång
AG3
Additioner och subtraktioner inom 10–19, med tiotalsövergång
AG4
Additioner och subtraktioner inom 20–99
AG5
Räknesättens innebörd, addition och subtraktion
AG6
Multiplikationstabellen
AG7
Generaliserad multiplikationstabell
AG8
Divisionstabell och generaliserad divisionstabell
AG9
Räknesättens innebörd, multiplikation och division
Alla diagnoserna bygger på att eleverna behärskar diagnosen Förberedande aritmetik (AF). Att behärska diagnoserna inom AG utgör i sin tur förutsättning för att eleverna ska kunna gå vidare med diagnoserna Aritmetik, skriftlig räkning (AS) och diagnoserna Aritmetik, utvidgad (AU).
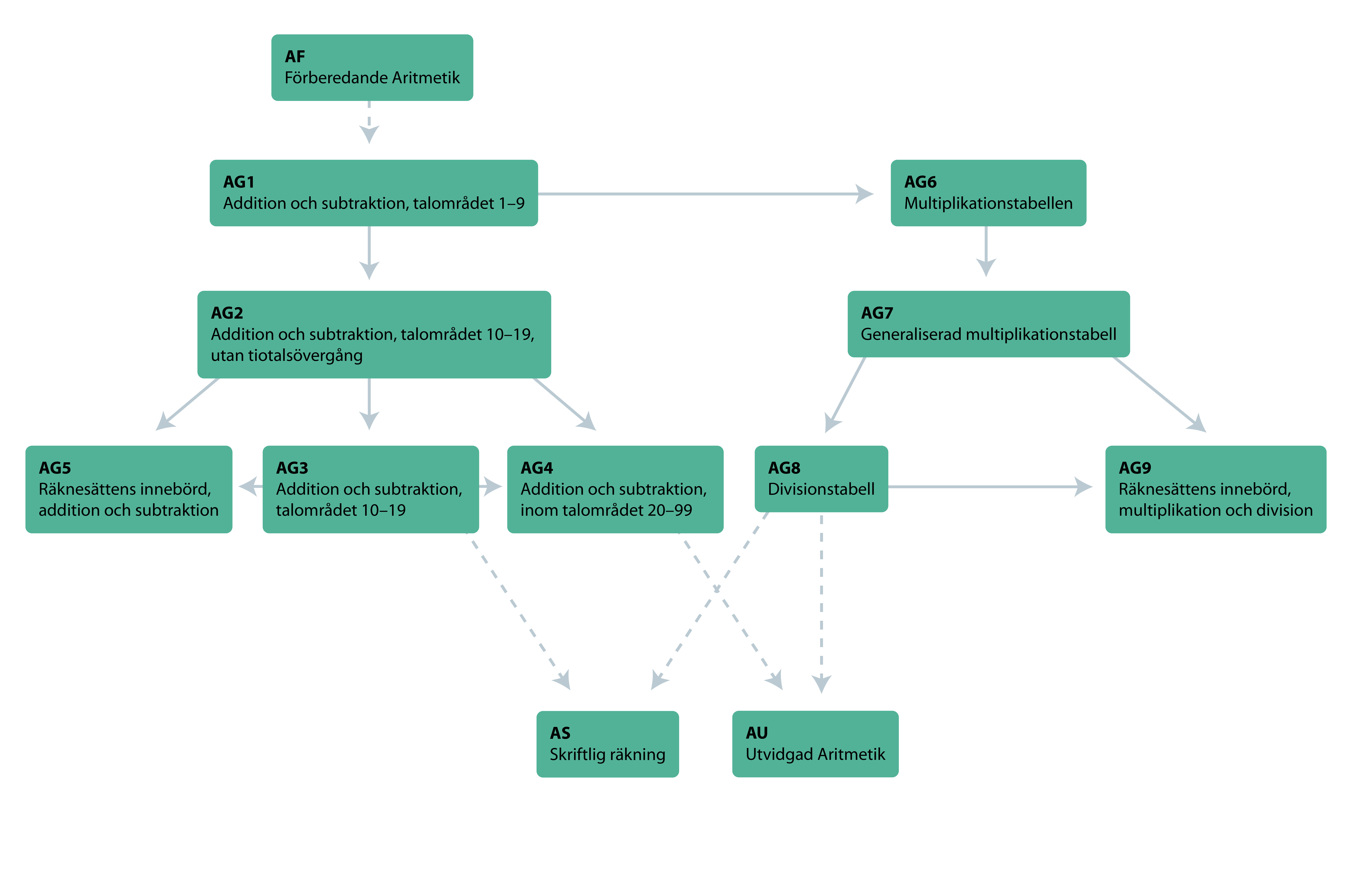
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Genom att följa pilarna i strukturschemat kan du t.ex. se att diagnos AG1 innehåller förkunskap till AG2, AG3, AG5 och AG6. På motsvarande sätt innehåller AG7 förkunskaper till AS4, AG8 och AG9. Det här betyder att en elev som inte klarat uppgifterna i AG2 kanske ännu inte behärskar alla uppgifter i AG1.
När det gäller AS2, alltså skriftlig subtraktion, så krävs förkunskapen AG3 om man använder lånemetoden. Om man istället använder utfyllnadsmetoden så räcker det med förkunskapen AG2. På motsvarande sätt kan du genom att följa pilarna baklänges se vilka förkunskaper som krävs för att behärska en viss typ av uppgift.
Grundläggande Aritmetik. AG
Didaktiska kommentarer till delområdet AG
En del av syftet med undervisningen i matematik är att eleven ska abstrahera, alltså lämna det konkretiserande arbetet och utföra matematiska operationer i huvudet. Det som diagnostiseras med AG diagnoserna är om eleverna nått detta stadium i sin utveckling inom området. För de elever som ännu inte har abstraherat och därmed inte klarat vissa delar av en diagnos AF krävs en ny inlärning. Denna inlärning kräver ofta en konkretisering. Men avsikten är då fortfarande att de ska förstå idén, alltså att de har abstraherat. Detta innebär att uppgifterna i de här diagnoserna ska lösas som huvudräkning, inte med hjälp av fingrar eller konkretiserande material. Det är därför viktigt att observera eleverna medan de gör diagnosen. Eftersom eleverna bör behärska de här uppgifterna i huvudet och på rimlig tid, är det viktigt att notera vilka elever som använder orimligt lång tid för att lösa uppgifterna, använder fingrarna eller i övrigt saknar flyt i sitt räknande. Dessa elever bör följas upp.
God taluppfattning inom grundläggande aritmetik
För att kunna utföra beräkningar, såväl i huvudet som med skriftliga metoder, behöver eleverna ha en god taluppfattning. En central del av denna taluppfattning är att eleverna behärskar de s.k. tabellerna för addition, subtraktion, multiplikation och division med flyt. En god taluppfattning inom grundläggande aritmetik omfattar bland annat följande delar:
• En känsla för hur tal är uppbyggda
Det gäller t.ex. att känna till talens ordning och talens grannar såsom att 6 + 1 = 7 eftersom 7 är talet efter 6 och att 8 – 7 = 1 eftersom talen 7 och 8 är grannar. Det gäller också att känna till uppbyggnaden av vårt positionssystem med basen 10, till exempel att talet 18 är komponerat av 1 tiotal och 8 ental och 35 av 3 tiotal och 5 ental. Eleverna behöver också behärska 10-tals- och 100-talsövergångarna såsom 8 + 3 = 11 och 11 – 2 = 9, vilket senare ska generaliseras till 98 + 3 = 101 och 101 – 2 = 99.
• De grundläggande räknelagarna
De grundläggande räknelagarna är de kommutativa och associativa lagarna samt den distributiva lagen. Det är med hjälp av dessa lagar man kan analysera tal och dela upp dem i termer och faktorer. Det är på dessa lagar de viktigaste aritmetiska operationerna bygger. Exempel på den associativa lagen är att 8 + 7 kan beräknas genom att talet 7 delas upp i 2 + 5 att 8 + 2 = 10. Detta ger i sin tur 8 + 7 = 8 + 2 + 5 = 10 + 5. På motsvarande sätt kan man beräkna 28 ∙ 25 genom att dela upp 28 i 7 ∙ 4 = 28 och 4 ∙ 25 = 100. Man får då 28 ∙ 25 = 7 ∙ 4 ∙ 25 = 7 ∙ 100.
De grundläggande räknelagarna kan också användas i följande situationer. Det är lättare att beräkna 5 + 32 som 32 + 5, enligt den kommutativa lagen. Det är också lättare att beräkna 8 ∙ 53 ∙ 25 som 8 ∙ 25 ∙ 53 = 200 ∙ 53 och 4 ∙ 98 som 4 (100 – 2 ) = 400 – 8. För den som vill bli duktig i huvudräkning är det av stort värde att behärska denna typ av operationer och det krävs att man kan utföra dem i huvudet och med flyt.
• Tals avrundning
Vid all beräkning är det viktigt att kontinuerligt kunna göra en rimlighetsbedömning av det man gör. För den som kan göra bra avrundningar av tal är det också enkelt att genom överslagsräkning göra lämpliga rimlighetsbedömningar. Detta ger samtidigt en säkerhetskänsla under hela beräkningen. Ett exempel på detta är att 32 – 19 är ungefär lika med 30 – 20 = 10. Med en god taluppfattning kan man emellertid gå ett steg längre och avrunda till 32 – 20 = 12, vilket är 1 för lite. Ännu smartare kan det vara att addera 1 till båda talen, alltså att utnyttja att 32 – 19 = (32 + 1) – (19 + 1) = 33 – 20. Den känsla för tal som byggs upp på det här sättet, kan senare överföras till algebran.
Skriftlig räkning. AS
Delområdet AS omfattar följande elva diagnoser:
AS1
Addition av två tal i talområdet 0–1 999
AS2
Subtraktion av två tal i talområdet 0–999
AS3
Additions- och subtraktion, textuppgifter
AS4
Multiplikation där ena faktorn är ensiffrig inom talområdet 0–999
AS5
Division där nämnaren (divisorn) är ensiffrig inom talområdet 0–999
AS6
Multiplikations- och division, textuppgifter
AS7
Multiplikation med flersiffriga faktorer
AS8
Skriftlig division med tvåsiffrig nämnare
AS9
Addition och subtraktion av två tal i decimalform
AS10
Multiplikation av tal i decimalform
AS11
Division av tal i decimalform
Arbetet med de här diagnoserna förutsätter att eleverna har förkunskaper från delområdet grundläggande aritmetik (AG).
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Här framgår vilka förkunskaper från grundläggande aritmetik (AG), som krävs för att kunna utföra skriftliga beräkningar. Det framgår även att AS1 och AS2 är förkunskaper till AS3 och att AS4 och AS5 är förkunskaper till AS6. Den här strukturen visar också att elevernas möjligheter att lyckas med diagnoserna i AS är i hög grad beroende av att de behärskar de kunskaper som diagnostiseras i AG.
AS9, AS10 och AS11 kräver även förkunskaper från RD4 och RD5 alltså att eleverna har en taluppfattning om tal i decimal form och att de kan lösa enklare beräkningar i huvudet för att göra rimlighetsbedömningar. Vidare behövs förkunskaper från motsvarande diagnoser inom AS1, AS2 respektive AS4 och AS5 för skriftlig räkning inom de naturliga talen.
Didaktiska kommentarer till delområdet AS
Som framgår av kursplanen är det inte tillräckligt att en elev kan räkna i huvudet eller med miniräknare. Eleven ska också behärska skriftliga metoder. En rimlig tolkning av detta är att alla elever ska ges en möjlighet att lära sig någon skriftlig metod (algoritm) för addition, subtraktion, multiplikation och division.
Vad menas med en skriftlig metod? Med utvecklingsbar metod menas att tillvägagångssättet är effektivt och generellt användbart. Det innebär att alla uppgifter, åtminstone inom talområdet 0–1 000, ska vara lösbara med metoden ifråga, inte bara vissa speciellt utvalda uppgifter.
Just det faktum att det räcker med en enda metod för att behärska en viss uppgiftstyp, är det som skiljer skriftlig räkning från huvudräkning. För att bli en bra huvudräknare måste man behärska en rad olika metoder (som var och en ofta är en typ av algoritm), eftersom metoden ofta måste väljas utgående från den typ av uppgift som för tillfället ska lösas. Vid skriftlig räkning räcker det däremot att behärska en enda metod (algoritm) för respektive räknesätt.
I kunskapskrav för godtagbara kunskaper i årskurs 3 finns följande: Vid addition och subtraktion kan eleven välja att använda skriftliga räknemetoder med tillfredsställande resultat när talen och svaren ligger inom heltalsområdet 0–200. Detta är ett högt ställt krav med tanke på att alla de deloperationer som förekommer i ett större talområde även förekommer i detta begränsade talområde.
För en elev som lärt sig en algoritm mekaniskt alltså utan djupare förståelse kan det vara svårt att byte metod. Detta är speciellt viktigt att uppmärksamma när en invandrad elev tidigare lärt en annan algoritm än klasskamraterna. I olika kulturer används olika metoder för skriftlig räkning. I varje kultur anses just deras metod vara den bästa. Detta bör tolkas så att det inte finns någon metod som är den generellt sett bästa. Alla metoder har sina för- och nackdelar. Däremot är det viktigt att de metoder eleverna lär sig är funktionella, och att de fungerar för att lösa alla uppgiftstyper inom respektive räknesätt.
Oberoende av vilka metoder för skriftlig räkning man väljer att erbjuda eleverna, kräver dessa metoder lämpliga förkunskaper, så att de deloperationer eleverna ska utföra kan utföras med flyt. För att en elev t.ex. ska kunna använda lånemetoden i subtraktion med flyt bör hon behärska den stora subtraktionstabellen och för att kunna använda utfyllnadsmetoden i subtraktion räcker det om hon behärskar tabellen upp till 10.
Utvidgad aritmetik. AU
Delområdet AU omfattar följande tio diagnoser som är grupperade i tre delar, negativa tal, potenser och närmevärden:
AUn1
Negativa tal, taluppfattning
AUn2
Negativa tal, addition och subtraktion
AUn3
Negativa tal, multiplikation och division
AUn4
Negativa tal
AUp1
Potenser, grundläggande
AUp2
Potenslagar 1
AUp3
Potenslagar 2
AUp4
Kvadratrötter
AUp5
Potenser och kvadratrötter
Arbetet med de här diagnoserna förutsätter att eleverna har förkunskaper från delområdet Grundläggande aritmetik (AG).
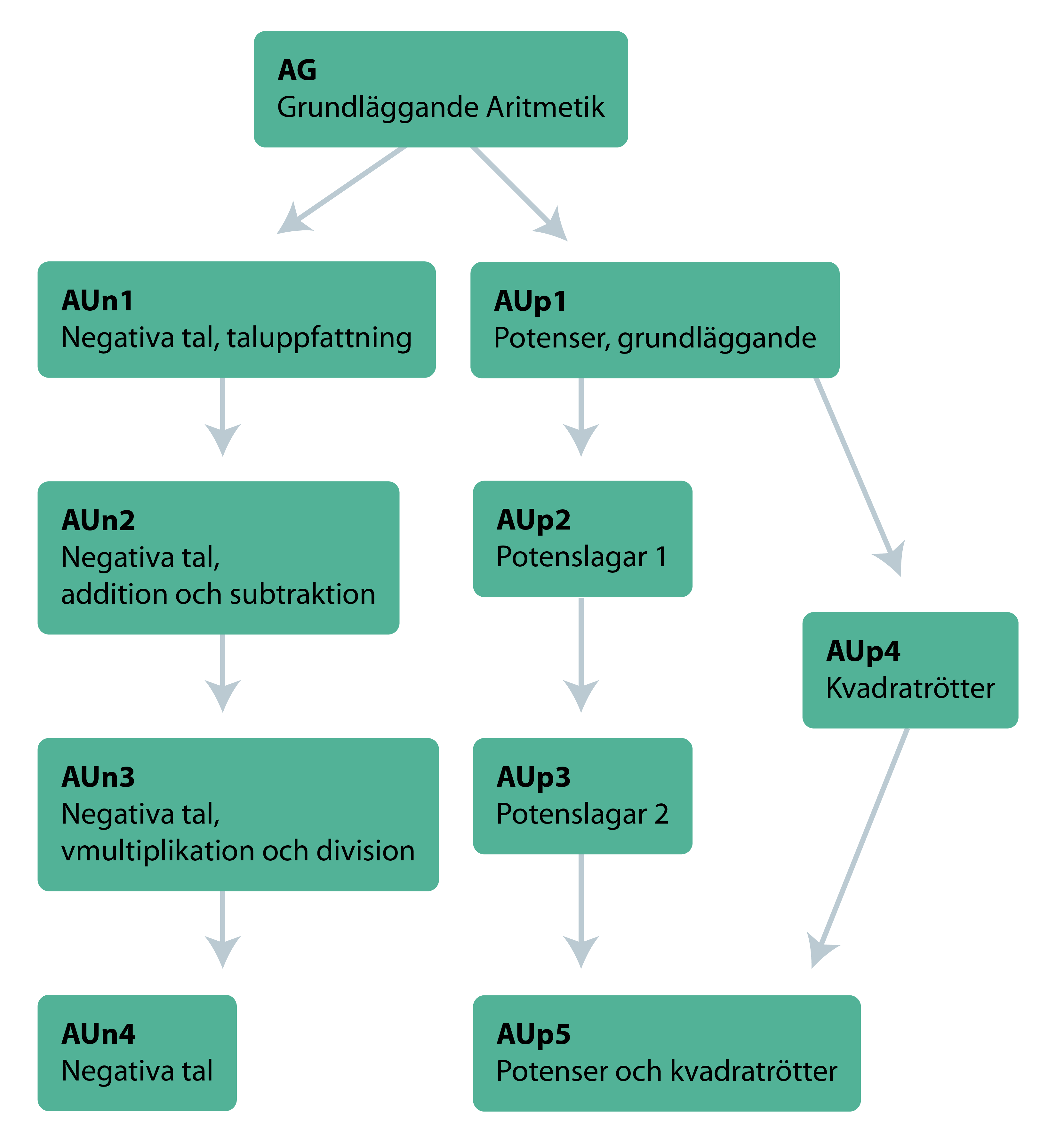
Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Här framgår att de olika delarna negativa tal, potenser och närmevärde inledningsvis är oberoende av varandra men alla kräver förkunskaper i grundläggande aritmetik.
En hel del av uppgifterna på de här diagnoserna är centrala förkunskaper på flera program inom gymnasieskolan. Även om alla elever inte behöver behärska samtliga dessa uppgifter så är diagnoserna viktiga. Diagnoserna ska kunna användas för att ge stöd vid bedömning av de duktiga eleverna.
Sambandet mellan de olika diagnoserna ser du
i strukturschemat nedan. Genom att följa pilarna i strukturschemat kan du till exempel se att diagnosen AU1 innehåller förkunskaper till AU2, att AU2 innehåller förkunskaper till AU3 o.s.v.
På motsvarande sätt innehåller AUp1 förkunskaper till AUp2, att AUp2 innehåller förkunskaper till AUp3, o.s.v. Ett avsteg från detta är AUp4 som fordrar förkunskaper från AUp1 och ger förkunskaper till AUp5.
Didaktiska kommentarer till delområdet AU
De negativa talen
Det är en ny utmaning för eleverna när talområdet utvidgas till att omfatta även de negativa talen. Det gäller att eleverna får en grundläggande förståelse för hur man opererar med de negativa talen, och hur man generaliserar räknelagarna, innan de lär sig regler som annars kan verka förbryllande.
De negativa talen dyker upp i en rad olika situationer, bland annat som svar till vissa ekvationer såsom x + 1 = 0 och 2x + 7 = 3 eller som koordinater på grafen till y = 3 – 2x. En förutsättning för att eleverna med framgång ska kunna arbeta med negativa tal, är att de förstår vad ett negativt tal är och vilka egenskaper de negativa talen har. Många av de svårigheter som uppstår, till exempel, vid multiplikation av två binom, beror på att eleverna inte förstår vad de gör. Det lönar dig därför att ägna lite tid åt att reda ut innebörden av detta, så att eleverna senare kan använda operationerna på ett korrekt sätt och utveckla sin förståelse.
De negativa talen −1, −2, −3, −4, −5 …. är de motsatta talen till 1, 2, 3, 4, 5 …, vilket innebär att 5 + (−5) = 0. Om man på tallinjen speglar ett naturligt tal i punkten 0, så får man motsvarande negativa tal. Som framgår av figuren så är −5 spegelbilden till 5. Eftersom eleverna redan vet att 5 – 5 = 0, bör man nu koppla samman de här två erfarenheterna, vilket ger det användbara sambandet 5 – 5 = 5 + (−5).
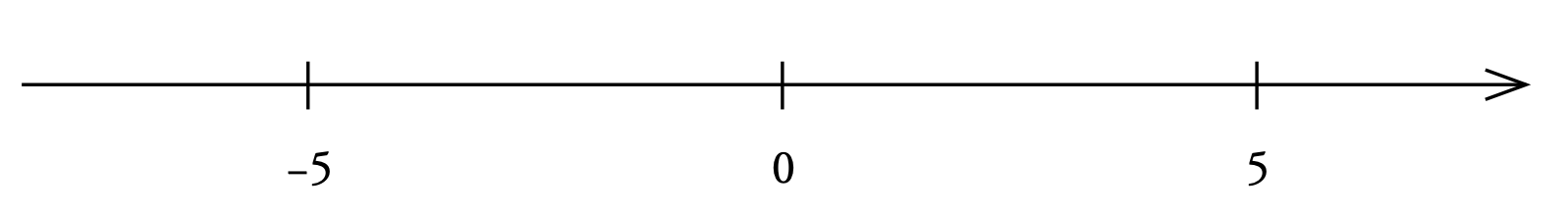
En konsekvens av detta är att uttryck som 4x – 5 – 2x + 6 kan skrivas 4x + (−5) + (−2)x + 6. Eftersom den kommutativa räknelagen gäller vid addition (men inte vid subtraktion) kan termerna byta ordning. Detta förklarar varför man har rätt att skriva det här uttrycket som 4x + (−2)x + 6 + (−5) = 4x – 2x + 6 – 5 = 2x + 1.
För att undvika sammanblandning mellan det minustecken som betecknar ett negativt tal och det minustecken som betecknar subtraktion är det ofta lämpligt att skriva talet −6 som (−6).
Elever som i årskurs 1 har lärt sig förstå kopplingen mellan subtraktion och öppen utsaga, kan nu använda den strategin även vid subtraktion av negativa tal.
Subtraktionen 6 – (−4) kan ses som en öppen utsaga, nämligen (−4) + __ = 6, vilket är avståndet på tallinjen från (−4) till 6 alltså 10.
Subtraktionen (−6) – (−4) kan ses som den öppna utsagan (−4) + __ = (−6), vilket är avståndet från (−4) till (−6) på tallinjen (i negativ riktning) alltså (−2).
En bra regel, som alltid fungerar, är annars att subtraktion av ett negativt tal är detsamma som en addition av det motsatta talet. Det betyder att (−6) – (−4) = (−6) + 4.
Subtraktioner som 6 – (−4) kan också lösas med hjälp av lika tillägg. Idén är detsamma som att 32 – 19 = 33 – 20 = 34 – 21. Om man adderar samma tal till båda termerna i en subtraktion så förändras inte differensen. På motsvarande sätt kan man addera 4 till båda termerna i subtraktionen 6 – (−4) vilket ger 6 + 4 – (−4) + 4 = 10 – 0.
Multiplikation och division med negativa tal
Den enklaste multiplikationen med ett negativt tal är av typen 3 ∙ (−4) som i sin tur är lika med (−4) + (−4) + (−4) = (−12). På motsvarande sätt är \(\frac{-12}{3} = 3 \cdot \frac{-4}{3} = (-12)\)
därför att \((-12) = (-4) + (-4) + (-4) = 3 \cdot (-4)\)
. Eftersom multiplikation är kommutativ gäller det även att (−4) ∙ 3 = 3 ∙ (−4) = (−12).
Att multiplicera två negativa tal är lite svårare. För att beräkna produkten (−3) ∙ (−4) kan man börja med att addera talet (−3) ∙ 4 vilket ger (−3) ∙ (−4) + (−3) ∙ 4. Genom att bryta ut (−3) kan man skriva om detta som (−3)[(−4) + 4] = (−3) ∙ 0. Eftersom summan av de två talen är noll måste de två talen (−3) ∙ (−4) och (−3) ∙ 4 vara motsatta tal. Vi vet emellertid redan att (−3) ∙ 4 = (−12). Alltså är det motsatta talet (−3) ∙ (−4) = 12. På motsvarande sätt är \(\frac{-12}{-4} = (-3) \).
Det är genom att resonera så här med eleverna och göra dem förtrogna med matematikens uttrycksformer som de lär sig matematik såsom att operera med negativa tal. Detta underlättar även förståelsen för de formler man så småningom kommer att använda.
Diskussioner av det här slaget som hjälper eleverna att förstå formler som \( (-a) \cdot (-b) = ab \) och \(\frac{-a}{-b} = \frac{a}{b} \) eller att \(\frac{a}{(-b)} = \frac{(-a)}{b} \). Detta leder i sin tur till en större säkerhet när de ska arbeta med algebra.
Grundpotensform
Med hjälp av grundpotensform kan talet 3 000 skrivas som \( 3 \cdot 10^{3}\), talet 3 900 som \( 3,9 \cdot 10^{3}\) och talet 3 980 som \( 3,98 \cdot 10^{3}\). På motsvarande sätt som man kan skriva 1 000 som \(10^3\), och 100 som \(10^2\) och 10 som \(10^1\) kan man skriva 0,1 som \(10^{-1}\), 0,01 som \(10^{-2}\) och 0,001 som \(10^{-3}\). Det betyder att man även kan skriva små tal i grundpotensform. Talet 0,00345 kan skrivas som 3,45 ∙ 0,001 eller i grundpotensform \( 3,45 \cdot 10^{-3}\).
Det innebär t.ex. att protonens massa kan skrivas som \(1,67 \cdot 10^{-27}\) kg.
Ett alternativ till att använda grundpotensform är prefixen. Istället för att skriva \(4 \cdot 10^{9}\) watt kan man skriva 4 gigawatt (GW). På motsvarande sätt kan man skriva \(3 \cdot 10^{6}\) volt som 3 megavolt (MV), \(5 \cdot 10^{-6}\) meter som 5 mikrometer (μm) och \(2 \cdot 10^{-9}\) sekunder som 2 nanosekunder (ns). Arbetet med detta bör ske i samverkan med NO−ämnena. Det här handlar om att använda matematikens uttrycksformer.