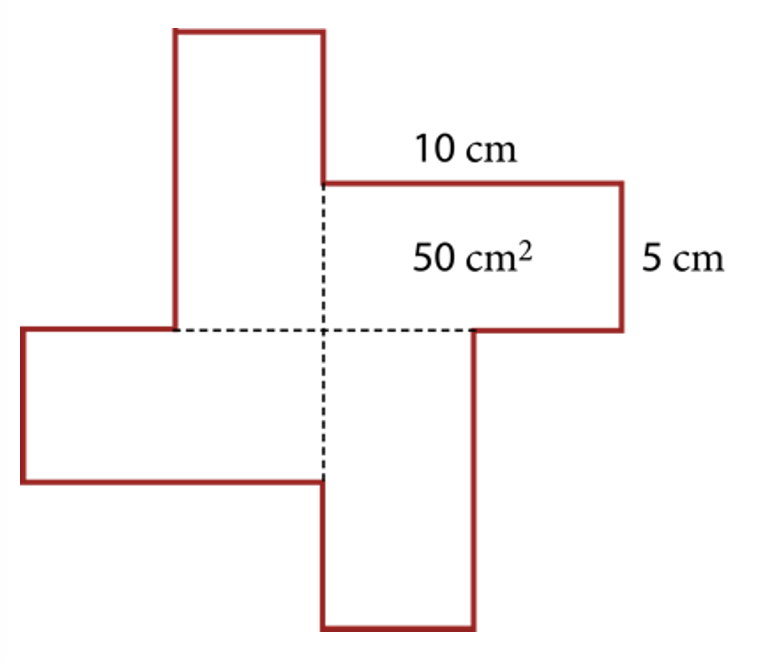
Jultomten vill baka pepparkakor som har formen av en månghörning där de fyra längre sidorna är dubbelt så långa som de åtta kortare sidorna. Alla vinklar i månghörningen är räta och figurens area är 200 cm². Vilken är månghörningens omkrets?
Svar: 80 cm
Lösning: Pepparkakan delas i fyra lika stora rektanglar med arean 50 cm². Den korta sidan är x och den långa sidan är då 2x. Det ger ekvationen 2x² = 50cm². Det ger x² = 25. Den korta sidan är då 5 cm lång och den långa sidan 10 cm lång. Det finns fyra långa sträckor och åtta korta sträckor. Detta ger omkretsen: (4 · 10 + 8 · 5) cm = 80 cm.