- Lösningar har kommit från:
Tindra A. Varberg.
Anton K. i 9:2 och Mina F. på Kunskapsskolan Kista.
Oxledsskolan i Sävedalen, åk 3 (Lärare: Paula Kern).
Klass 1A och 1B på Långsättersskolan i Nyköping (lärare: Josefin Thorsten).
Två elever i klass 5a på Skånhällaskolan.
Gruppen ”Utmanande matte” inom elevens val, åk 6-9, på Fjällenskolan i Järfälla (lärare: Annika Lundin).
Klass 3-4, lila Grossbolskolan i Forshaga.
Vera P. 6H Vasa Real, Stockholm.
Lösning på problem 1
Svar: Den mörka triangeln (den andra figuren från vänster).
”Uppgift 1 är glasklar för eleverna. Alla svarar i kör att det är triangeln hon menar när jag läst påståendena.” – skriver Josefin T.
Lätt även för de yngsta elever när de får problemet tydligt presenterat.
Observera att ordningen av Marias tre påståenden saknar betydelse och att det första påståendet egentligen är onödigt, allt det säger framgår också av det tredje påståendet.
Lösning på problem 2
Svar: 2 katter ljuger (och två säger sanning).
Ett knivskarpt resonemang från elever i Fjällenskolan:
”Trixet var att inse att det inte handlar om vem som ljuger, utan hur många. Vi undersökte två olika antaganden; att Tiger ljuger respektive att Tiger talar sanning. Vid båda antagandena ”nystade” vi fram om de andra katterna ljög eller talade sanning. Båda antagandena gav att två katter ljuger och att två talar sanning (men att det är olika katter i båda fallen).”
Vet man huruvida Tiger säger sanning eller ljuger, så kan man ”nysta” fram hur alla de andra katterna gör. Detta garanterar att det inte finns fler än 2 möjligheter.
Vi har fått ett bildbevis på att även elever på Långsättersskolan undersökte båda möjligheterna:

En pil från Tiger till Simba markerar här att Tiger säger att Simba ljuger. Detta i sin tur leder till slutsatsen att antingen Tiger säger sanning och i så fall Simba ljuger eller Tiger ljuger och i så fall Simba säger sanning. Alltså en av dessa två katter ljuger och en säger sanning. Observera att pilen i motsatt riktning skulle betyda en annan sak som ändå leder till samma slutsats. Pilen mellan Simba och Tiger och en mellan Murre och Puma ger att två av dessa fyra katter ljuger och två säger sanning.
Lösning på problem 3
Svar: Max ljuger. Isak och Oskar säger saning.
Problemet är på flera sätt svårare än problem 2. Redan övergången från det vanliga språket till det formella, matematiska språket bjuder på fallgropar. Dessutom handlar det inte bara om logik utan också lite om geometri, triangelolikheten i alla fall. Dessutom hanterar vi i vårt resonemang olikheter. Observera att det finns skillnader mellan hantering av ekvationer och hantering av olikheter. Angående triangelolikheter, i en triangel med sidolängder a, b och c gäller bl.a. a < b + c men även om vi har godtyckliga tre punkter med avstånden a, b och c, som kanske bildar en triangel, kanske ligger på en rät linje, så gäller i alla fall de svaga olikheterna a <= b + c etc..
Från Fjällenskolan kommer följande:
”Eftersom Max och Oskar säger samma sak även om båda utgår från sig själva och Isak säger något annat, måste Isak ljuga.”
Ni har klarat er över två fallgropar och fallit i den tredje.
1. Ordet ”jag” kan betyda olika personer (eller talande fåglar) beroende på vem som säger det, när Max säger det betyder det Max, när Oscar säger det betyder det Oscar.
2. Det är alltid lika långt från Oscar till Max som från Max till Oscar, därför första delen av Max utsaga betyder ändå samma sak som första delen av Oscars utsaga.
3. De sista tre ord: ”som från Isak” betyder olika saker i Max och i Oscars utsagor. Det är en förkortning av ”så långt som jag bor från Isak” och ”jag” betyder Max i ena fallet och Oscar i det andra.
Max och Oscar säger alltså olika saker. Vi ska sedan bevisa att de motsäger varandra.
Ungefär likadant misstag gör Mina. Några andra ger rätt svar men utan förklarning.
Vera har skickat oss bilder av två konstellationer i vilka Isak och Oscar säger sanning medan Max ljuger.
Vi har snyggat upp bilderna lite och lagt till en bild av en tredje sådan konstellation. Ta en, vilken som helst av dem och undersök hur de tre koltrastarnas utsagor stämmer på dem.
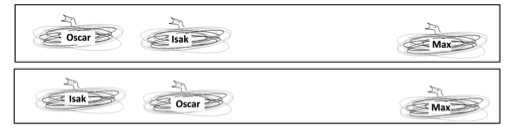

Undersökningarna bekräftar att Isak och Oscar säger sanning medan Max ljuger. Men finns det konstellationer för vilka andra två koltrasternas utsagor är sanna, kanske alla tres?
Vi ska uttrycka koltrastarnas utsagor med matematiska formler och använda triangelolikheten.
Låt a vara avståndet mellan Isak och Max,
b – mellan Isak och Oscar
och c – mellan Max och Oscar.
Nu kan fåglarnas utsagor utryckas kort:
Isak: a > 2 b
Max: c > 2 a
Oscar: c > 2 b
Anta att Isak och Max säger sanning.
Ledvis addition av Isacs och Max olikheter ger: a + c > 2 b + 2 a
som i sin tur ger: c > 2 b + a > a + b vilket strider mot triangelolikheten
Anta att Oscar och Max säger sanning.
ledvis addition av Oscars och Max olikheter ger: 2 c > 2 b + 2 a
division av både sidor med 2 ger: c > b + a vilket strider mot triangelolikheten
Om minst två av koltrastarna säger sanning så måste det vara Isak och Oscar.
Innehåll: LR
