- Lösningar har kommit från:
David W. Svenarums skola
En liten grupp i klass 8C på Önneredsskolan (insänt av Ellen L.)
Klass 1 på Hästöskolan, Karlskrona (med Victoria Olsson, som är VFU-student)
Marcus R.
Linnea G.
Moa F.
Christian och Alyaa i Bäckadalsgymnasiet, Jönköping (lärare: Jakob Magnusson)
Klass 4B i Hammarlundens skola, Hammarö (lärare: Marcus Ringqist)
Isak, Celina och Tina i klass 7A på Hästveda skola, Hässleholms kommun (lärare: Caroline Hansson)
Fanny, Moa, Lovisa, Arvid, William, Jonathan, Ludvig, Tilda, Alice, Nico, Trolle, Selma, Katrine, Paula, Isac, Matilda, Maja, Ebba, Sabbi, Jvahl, Julia och Ella i 6C, Rydbergsskolan i Lerum (lärare: Marian Sandström)
Vilma M. och Thelma H. i 7B Åsenskolan Anderstorp
Jacob N. åk 8 på Eddaskolan i Täby (lärare: Kristian Hultman Abbing)
Tuna i klass 1, Jennifer, Simon, Kelly, Alvin och Elin i klass 2 samt Jonna i klass 3 i Örsjö skola, Nybro kommun
Lösning på problem 1
Svar: Minst 4 barn, 2 pojkar och 2 flickor
Eftersom det talas om barn i en familj så kan vi anta att det finns minst ett barn där.
Varje barn har minst en bror och en syster, alltså måste det finnas minst en pojke och en flicka i familjen.
Eftersom varje pojke har en bror, måste det finnas minst två pojkar i familjen.
Eftersom varje flicka har en syster, måste det finnas minst två flickor i familjen.
Maja i Rydsbergskolan uttrycker det kort:
Alla ska ha en syster och en bror och en bror ska ha en bror till och en syster ska ha en syster till.
Fler än fyra barn behöver de inte vara. Finns det två pojkar och två flickor i syskonskaran så har varje barn en bror, en syster och ett syskon till.
Victoria Olssons lektionsbeskrivning:
Vi löste problemet med 1/3 av klassen som fick titta på problemet på tavlan och själva fundera och sen fick några elever visa sina lösningar på tavlan och de som inte höll med fick visa hur de hade tänkt. Till sist gick vi gemensamt igenom genom att eleverna själva fick agera syskon i familjen och på så vis kom vi alla överens om samma svar.
Lösning på problem 2
Svar: Benjamin. Den muffins som blir kvar kan inte vara en blåbärsmuffins.
Många har beskrivit hur pojkarna kan ta sina muffins:
En tar två lika, en två olika och den tredje ibland två lika, ibland två olika.
Ibland blir det en hallonmuffins kvar, ibland en kladdmuffins.
Eleverna i Önneredsskolan har sammanställt det i en tabell:
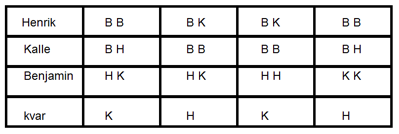
Tabellen har fyra kolumner utom den vänstra därför att det finns fyra olika sätt som pojkarna kan ta de första sex muffinsen på.
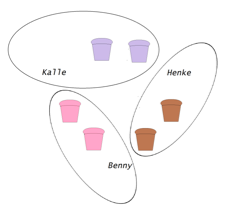
Det kan också visas i bilder:
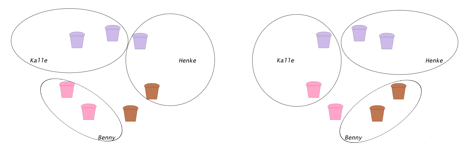
Om Benny tar två hallonmuffins, så tar Kalle två blåbärsmuffins och Henke en blåbärs- och en kladdmuffins (eftersom någon ska ta två olika).
Om Benny tar två kladdmuffins, så tar Henke två blåbärsmuffins och Kalle en blåbärs- och en hallonmuffins.
Om Benny tar en hallon- och en kladdmuffins, så finns det två möjligheter:
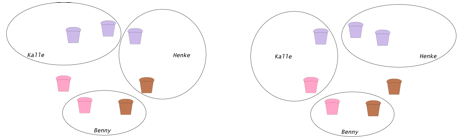
antingen tar Kalle två blåbärsmuffins och Henke en blåbärs- och en kladdmuffins eller tar Henke tvåblåbärsmuffins och Kalle en blåbärs- och en hallonmuffins.
Vi ser att i två fall blir en hallonmufins kvar och i två fall en kladdmuffins, aldrig en blåbärsmuffins. Önneredsskolans elevers slutsats är att Benjamin kan alltid ta den sista muffins.
Ett annat sätt att bevisa att en blåbärsmuffins inte kan bli kvar är ett motsägelsebevis:
Anta att en blåbärsmuffins kan bli kvar, då kan vi lika gärna lägga den undan från början och låta pojkarna ta av övriga sex muffins, två var av sina favoriter. Nu finns det två muffins av var och en av de tre sorterna. En pojke tar två lika, då återstår två av varje i de andra två sorterna.
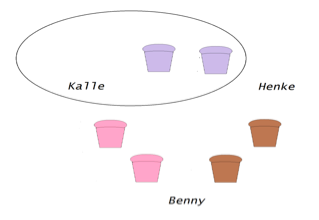
För en av de övriga pojkarna är bara en av dessa sorter hans favoriter, han tar båda två av den sorten och det återstår två muffins av den tredje sorten till den tredje pojken.
Varje pojke tar alltså två lika, vilket motsäger beskrivningen, en skulle ta två lika och en två olika. Det är uteslutet att en blåbärsmuffins blir kvar.
Lösning på problem 3
Svar: 84 liter.
Det har kommit flera rätta svar på denna fråga.
Akvariet, (vi antar att det har form av ett rätblock), dess storlek och proportioner bestäms av tre parametrar: längden L dm, bredden W dm och höjden H dm. De flesta som svarade med rätt volym, kunde också ange parametrarna.
Givna är tre ytmått: bottens area, B = 21 dm2, framsidans, F = 28 dm2 och gavelns, G = 12 dm2. Vi kommer att se att även dessa tre mått entydigt bestämmer akvariets storlek och proportioner men det är lite trixigare att utgå från dem än från L, W och H.
Vi vet att B = L∙W dm2, F = L∙H dm2 och G = W∙H dm2 alltså L∙W = 21, L∙H = 28 och W∙H = 12
Nu ska vi lösa problemet på två sätt:
Det första sättet är till hälften en gissning och till hälften ett resonemang. Vi gissar att de flesta tänkte på detta sätt. Vi antar att L, W och H är heltal. Då är L och W delare i 21, L och H delare i 28 och W och H delare i 12, alltså är L en gemensam delare till 21 och 28, W till 21 och 12 samt H en gemensam delare till 28 och 12. Vi chansar också att de gemensamma delarna är största gemensamma delare, alltså L = SGD (21, 28) = 7, W = SGF (21, 12) = 3 och H = SGD (28, 12) = 4.
Vi har tur, L = 7, W = 3 och H = 4 uppfyller ekvationerna: L∙W = 7∙3 = 21, L∙H = 7∙4 = 28 och W∙H = 3∙4 = 12. L, W och H kan vara 7, 3 och 4.
Volymen i så fall är L∙W∙H dm3 = 7∙3∙4 = 84 dm3, fast det är osäkert om det är den enda möjligheten.
I den andra metoden tar vi ekvationerna L∙W = 21, L∙H = 28 och W∙H = 12 och multiplicerar dem ledvis (L∙W) ∙ ( L∙H) ∙ (W∙H) = 21∙28∙12
L∙W∙L∙H∙W∙H = 21∙28∙12
L∙W∙H∙L∙W∙H = 21∙28∙12
(L∙W∙H) ∙ (L∙W∙H) = 21∙28∙12
V∙V = 21∙28∙12 = 7056
V = √7056 = 84
Lite smartare och utan en räknedosa kan vi räkna: V= √(21∙28∙12) = √(3∙7∙4∙7∙3∙4) = 3∙7∙4 = 84
Beräkningen av V är klar men vi är nyfikna på L, W och H. De är enkla att beräkna:
L = V/G = 84/12 = 7, W = V/F = 84/28 = 3, H = V/B = 84/21 = 4
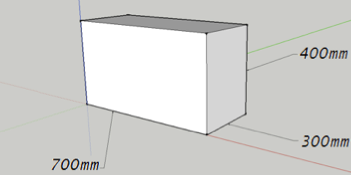
En perspektivbild av akvariet gjord av Jacob N. i Täby.
Innehåll: LR
