En stjärna med n antal spetsar: Rita en cirkel och fördela n punkter jämnt längst cirkelns rand. Starta i en av punkterna och dra ett streck till en punkt som ligger två steg åt höger. Fortsätt likadant tills du är tillbaka på den första punkten. Med 5 punkter på cirkeln skapas en 5-uddig stjärna. Om det inte fungerar så försök att gå rund cirkeln på var tredje punkt, eller var fjärde punkt.
För 6 punkter fungerar det inte. Eftersom 6 är delbart med både 2 och 3 kommer du vara tillbaka till din första punkt både när du testar varannan punkt eller var tredje punkt.
För alla heltal n ≥ 7 kommer det att finnas minst ett sätt att rita en stjärna eftersom det kommer att finns minst ett tal mindre än n som inte är en delare till n.
Alla stjärnor med udda antal spetsar går att rita genom att gå till varannan punkt eftersom talen inte är delbart med 2. Många kommer även att kunna ritas på andra sätt. Exempelvis är 7 inte heller delbart med 3 så det går att rita om man går till var tredje punkt. 7 är heller inte delbart med 4, men att gå till var fjärde punkt kommer att resultera i en likadan stjärna som när man går till var tredje punkt åt andra hållet.
Testa vidare med andra stjärnor. Om n är ett mycket stort tal och stjärnan ritas genom att gå till varannan punkt kommer den att snarare att likna en cirkel. Ett sätt att beskriva stjärnan är att först ange antal uddar, och sedan det tal man delar in sina hopp med. Exempelvis betecknas den 5-sidiga stjärnan som (5, 2). Om det andra talet inte är en delare till det första så kommer du slutligen att få en stjärna.
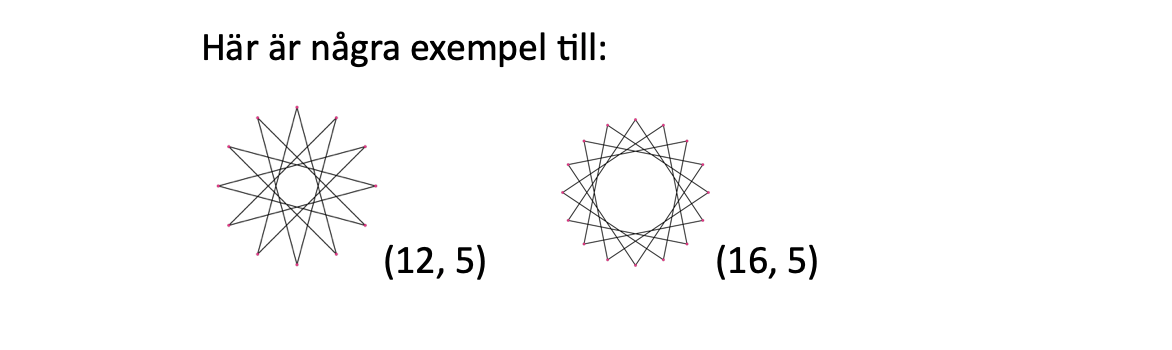
Här syns hur stjärnan passar in i cirkeln.
Bild hämtad från: https://www.slideshare.net/itsmedv91/star-polygons-application-of-cyclic-group/
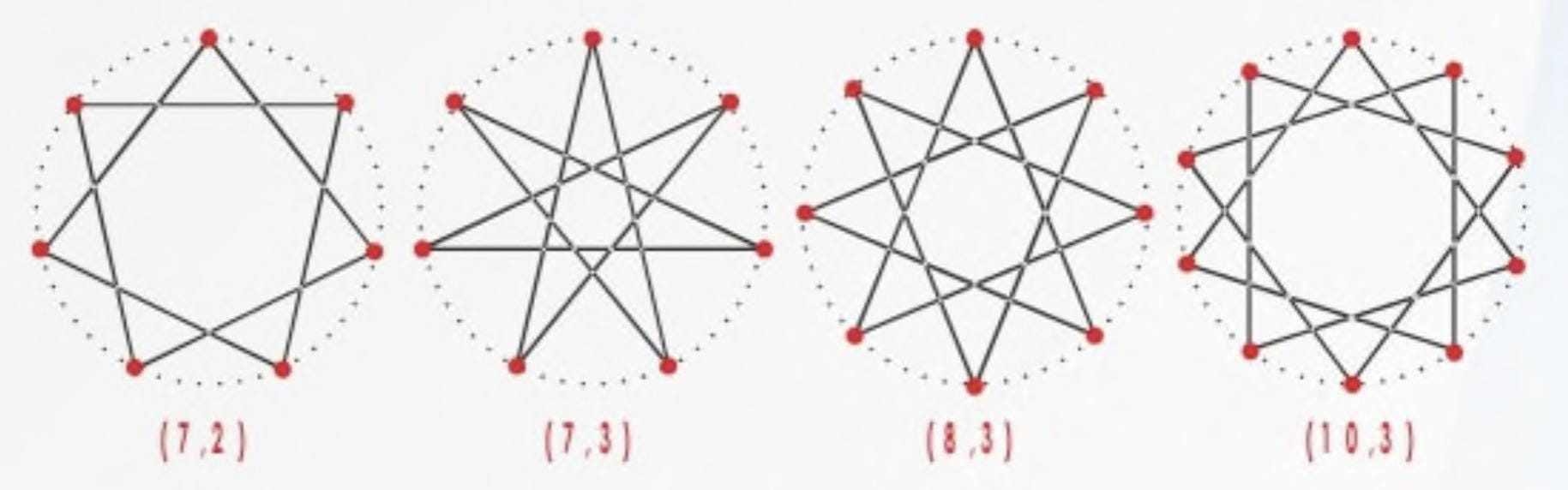
För den som vill läsa med om matematiken bakom:
https://en.wikipedia.org/wiki/Star_polygon/
https://professortiz.wordpress.com/2013/03/05/489/