Vi tackar
Hugo Dahlgren, Alexander Nyberg, Mou Beskow, Tyra Pihlgren, klass 5B, Kungsholms skola, Stockholm
Jack Filipsson och Melker Marcusson, klass 5, Långareds skola, Alingsås
Isac Melin, Melvin Hjort och Viggo Karlsson, Alingsås
Signe Ahlning och Ella Ahlberg, Alingsås
Felix och Lucas, Vibyskolan
Douglas Oredsson, åk 7, Markaryd
Ebba, Nina och Viktor, Mattegrupp, Paulinska skolan, Strängnäs
Eda Demir, Långareds skola, Alingsås
Alva Ahlgning, Långareds skola, åk 6, Alingsås
Mattegrupp åk 2, Almby skola, Örebro
Elias Eriksson, åk 5
Ester Jakobsson, åk 5a, Askimsskolan, Göteborg
Agnes Q, Klara H och Lina åk 6 Grimstaskolan Upplands Väsby
Sebastian, Edit och Isak åk 8 Grimstaskolan Upplands Väsby
Eleverna på Elevens val mattetävlingar. Grimstaskolan Upplands Väsby
som har skickat in lösningsförslag eller svar på minst ett av problemen.

Rätt svar: 2400 meter
Det finns många fina lösningar på problemet. Så här skriver Signe Ahlning och Ebba Ahlberg från Alingsås;
Det är 600 m mellan tre soptunnor, därför är det 300 m mellan varje soptunna. Det är 9 soptunnor och 8 mellanrum, och därför blir det 300 x 8 = 2400 m
Åk 2 i Almbyskolan i Örebro har skickat in följande bild med lösning:

De har också skrivit förklaringen: Det blir 2 avstånd mellan de tre första papperskorgarna. Alltså 300 + 300. Det blir 4 sträckor med 600 m, alltså 600×4. Totala sträckan mellan de nio papperskorgarna blir 2400 meter.
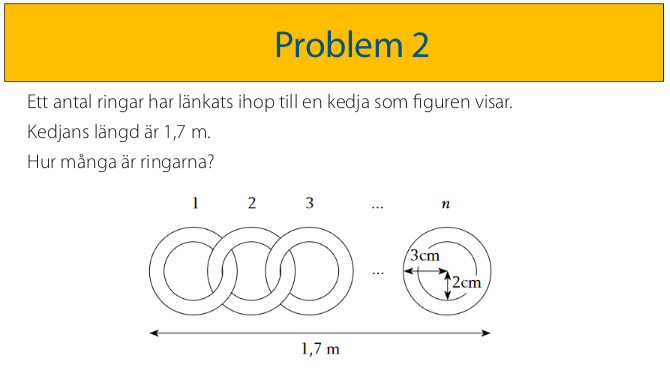
Rätt svar: 42 ringar
Jack Filipsson och Melker Marcusson, Långareds skola klass 5 har skickat följande lösning.
Den första ringen är 6 cm och sen blir resten 4 cm för när man kopplar ihop den förlorar man 2 cm.
170 – 6 = 164 den första ringen är 6 cm för det är den första ringen i kedjan.
164/4 = 41 nu vet vi att vi behöver 41 ringar.
41 + 1 = 42
Svar: Det behövs 42 ringar för att komma till sträckan 1,7 meter.
Douglas Oredsson, Markaryd, åk 7 har skickat följande lösning.
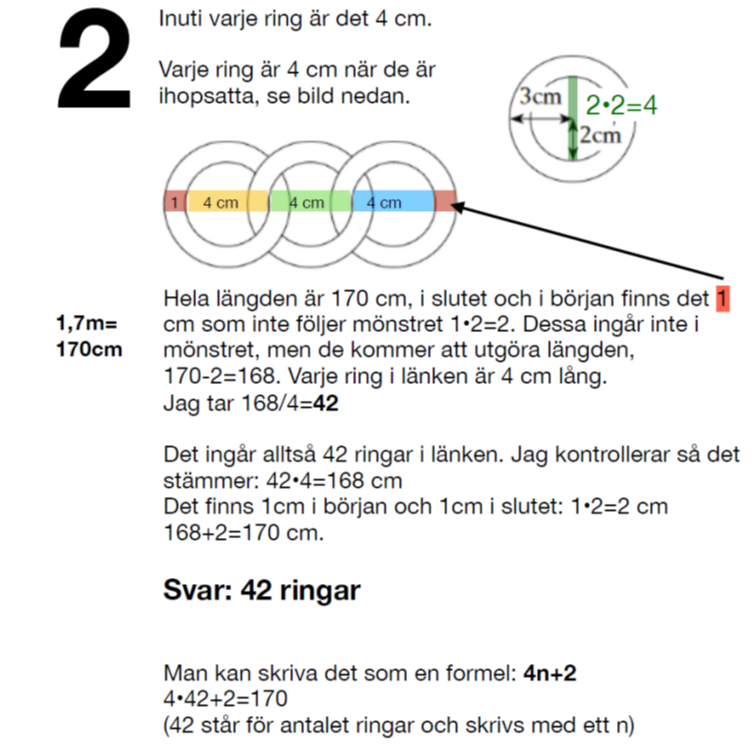

Rätt svar: c = 4
Man kan bilda sex tresiffriga tal genom att permutera a, b och c. Talen är abc, acb, bac, bca, cab och cba. Det ger:
2(a + b + c)·100 + 2(a + b + c)·10 + 2(a + b + c)·1 = 1554
(a + b + c)·100 + (a + b + c)·10 + (a + b + c)·1 = 777
a + b + c = 7
De tre siffrorna är 1, 2 och 4. Eftersom c ska var den högsta siffran så är c = 4.
Här visar vi svaret från Grimstaskolan, Upplands Väsby:
Genom att permutera dessa a,b,c får man 3+2+1=6 möjliga tal:
abc
acb
bac
bca
cab
cba
Genom prövning kom vi fram till att 1; 2 och 4 ger summan 1554.
124 + 142 + 214 + 241 + 412 + 421 = 1554.
Eftersom a<b<c måste c vara det största talet, alltså 4.
