Denna månad har fler än vanligt skickat in svar. Det skulle vara roligt om ni som bara skickar svarar även skriver ner era tankegångar så vi andra kan förstå hur ni har tänkt.
Ett stort tack till
Douglas Oredsson, klass 5, Markaryds skola, Markaryd
David Mihic, klass 4, Gårdstensskolan, Angered och Davids mamma
Max Kvarnström Barck-Holst, Elina Stegenberg och Nova i klass 3a, Tegelhagsskolan, Sollentuna
Jasmine och Agnes, klass 6, Emanuelskolan, Sjöbo
Puja och Emma, Nils, Liam Lind och Albin Hansson, Anton och Erik, Klara, Greta och Line, Oskar Gabrielsson och Erik Widahl, Hanna och Linnea, Liam och Kim, Olle, Elsa och Ida, samtliga i klass 6a Rydsbergsskolan, Lerum
Amanda, Ingrid och Lovisa åk 4–6, Amelie 6A, Samuel 6B, Einar och Max 6B, Ebba, Stina, Alexandra och Stella samtliga åk 4–6, Hedvig Eleonora skola, Stockholm
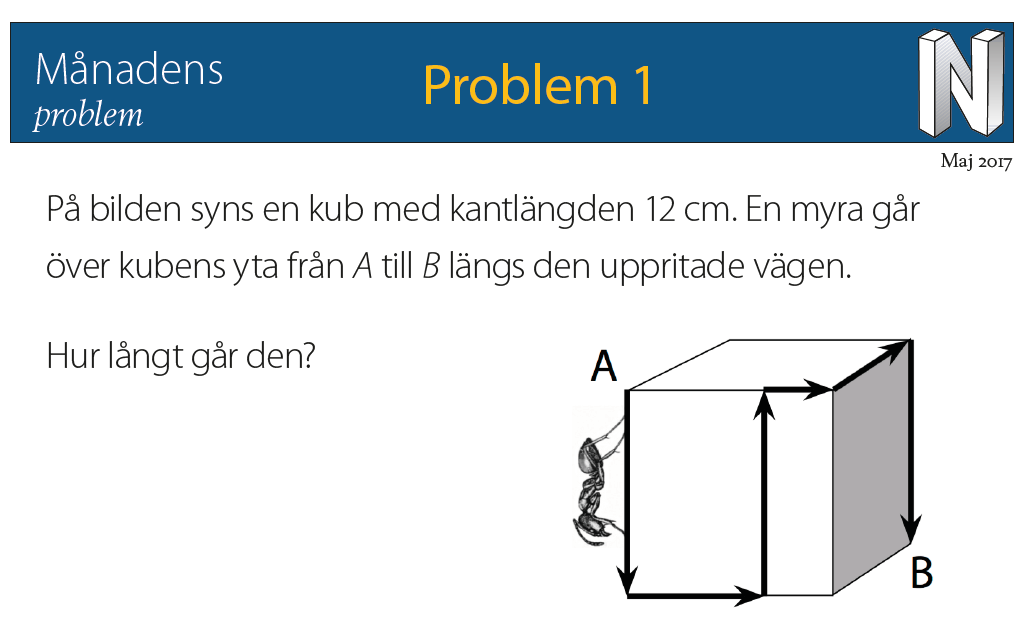
Lösning på problem 1
Svar: 60 cm
De flesta som har löst problemet har kommit fram till rätt svar. Amanda, Ingrid och Lovisa, på Hedvig Eleonora skola, skriver så här:
1) Vi börjar med att addera alla kantlängderna (12 · 4).
2) Sedan tänkte vi att de två vågräta pilarna på främre sidan blir en hel kantlängd, alltså 12 cm.
3) Vi adderade svaren i 1) och 2) och får 60 cm.

Lösning på problem 2
Svar: 2 + 2√2 ≈ 4,8
Det är bara Davids mamma som vet hur man ska beräkna längden av en diagonal i en kvadrat.
Ni övriga har ritat och konstaterat att den minsta sträckan blir att gå utefter två diagonaler och går två vågräta sträckor. Nils, på Rydsbergsskolan skriver: Att gå diagonalt är alltid kortare för att komma ner i rutnätet till samma höjd som målet och efter det finns en rak väg i målet. Svar: 1,4 · 2 + 1,4 · 2 = 4,8
Diagonalens längd går att bestämma med Pythagoras sats. För en rätvinklig triangel med kateterna a och b och hypotenusan c gäller att summan av kvadraterna på kateterna är lika med kvadraten på hypotenusan, a2 + b2 = c2


Lösning på problem 3
Svar: 16 längdenheter
Här är det flera av er som har testat er fram, men det är bara Douglas, på Markaryds skola, Einar och Max, på Hedvig Eleonora skola, Amanda, Ingrid och Lovisa, på Hedvig Eleonora skola som levererar rätt svar. Douglas bygger en kub av gröna piprensare, markerar starthörnet med en röd lapp, och visar med svarta piprensare hur myran måste gå för att villkoren ska var uppfyllda. Amanda, Ingrid och Lovisa ritar en kub och utefter dess kanter pilar för myrans väg. Hur gör man då ett resonemang utan att rita och bygga?

Innehåll: LT och SG
