Vi tackar:
Jakob Magnusson, Bäckadalsgymnasiet, Jönköping, som löste uppgifterna samma dag som de publicerades
Tage Johansson, klass 5B, Hagaskolan, Dalsed
Åk 5 och 6, Hedvig Eleonora skola, Stockholm
David Mihic, klass 4a, Gårdstensskolan, Angered och Davids mamma
Douglas Oredsson, klass 5, Markaryds skola, Markaryd
Ina Åman, klass 6, Kyrkhults skola, Olofström
Lydia, Klas Oscar, Hampus och Anton, Skuruskolans Kluringklubb, Nacka
William Lundberg

Lösning på problem 1
Svar: Den fjärde rektangeln har arean 15/4 och den stora rektangeln har arean 63/4
David gör en fin lösning där han jämför höjd och bas mellan de fyra rektanglarna. Jakob konstaterar i sin lösning att den fjärde rektangeln har samma höjd som rektangeln med area 5. Den i sin tur har samma bas som rektangeln med area 4. Alltså är förhållandet mellan de två rektanglarna 5:4. Samma förhållande gäller för den fjärde rektangeln och den med area 3. Det ger att fjärde rektangelns area är 5/4 · 3 = 15/4 och total arean är 63/4.
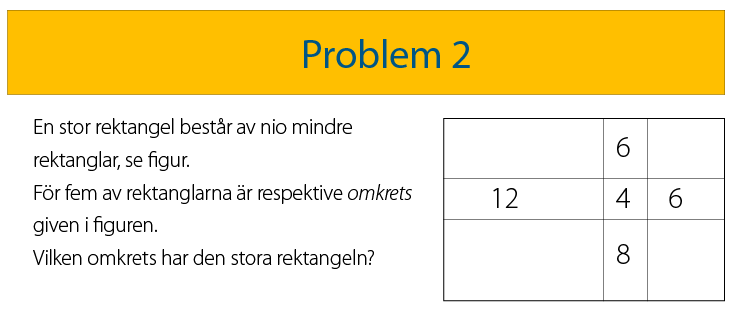
Lösning på problem 2
Svar: 28 längdenheter
Samtliga inskickade lösningar har kommit fram till rätt svar och de använder samma metod. Man utgår från att rektangeln med omkrets 4 är en kvadrat med sidan 1. Därefter faller övriga sidor ut automatiskt. Rektangeln med omkrets 12 har sidorna 1 och 5, rektanglarna med omkrets 6 har sidorna 1 och 2, rektangeln med area 8 har sidorna 1 och 3. Då har den stora rektangeln sidorna 8 och 6 och omkretsen är 2(8 + 6) = 28

Lösning på problem 3
Svar: 37 1/20 areaenheter
Jakob och Davids mamma är de enda som skickat in korrekta svar. Jakob skrev:
”Liknande problem som nummer 1. Rutan i mitten är 5/4 av 3. Rutan till höger om 1 är dubbel, liksom rutan till höger om 5 bör vara 10 och mittenrutan till höger bör vara dubbel mot centrumrutan. Rutan längst upp till vänster är 4/5 av 1.
Totalt blir detta:
4/5 + 1 + 2 + 3 + 15/4 + 30/4 + 4 + 5 + 10 = 16/20 + 225/20 + 25 = 12 + 1/20 + 25 = 37 1/20”
Innehåll: LT och SG
