- Vi tackar:
Elever i 6D på Käppala skola, Lidingö och deras lärare Jessica John
Markus C eller ”de coola kidsen”
Hilda B
Meja D, Tyra T, Vidar K och Theo S elever i åk 5b på Herrgärdsskolan i Västerås och deras lärare Mia Hasselgren
Douglas O i Båstad Montessori
Alice B, Dorotea M, Alba H och deras lärare Carin Bergdahl i Djupadalsskolan i Malmö
Elin J
Kristian M, Lucas F, Axel P och Simon T i klass 5 i Malsta skola
Lova och Vendela i 6b på Kastellegårdsskolan
David M i 3A, Långmosseskolan, Angered
Daniel E i Hvitfeldtska gymnasiet, matematikspets år 3
Alicia B och Cha S år 6 i Hannaskolan, Örebro och lärare Hanna Angel
samt Jacob m fl.
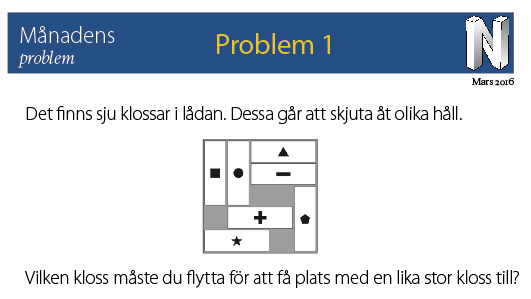
Lösning på problem 1
Svar: Kloss med + flyttas till vänster
För en lite svårare version se problem 1 i Månadens problem, januari 2014.
Lösning på problem 2
Svar: 5
Douglas har skickat oss en sådan bild. (Vi har numrerat bladen.)
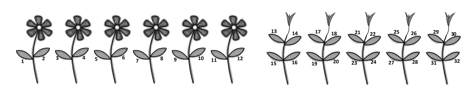
Man ritar sex växter med blommor och börjar rita växter med skott, räknar bladen och fortsätter att rita och räkna tills det blir 32 blad. Då räknar man skott och får svaret.
Problemet kan ges redan i förskolan/förskoleklass, kanske med mindre antal växter, och lösas som ovan. I stället för att rita allt på ett pappersark kan kort med växtbilder användas.
Elever på Käppala skola, har löst det på följande sätt (sammanfattat av läraren):
Det finns sex blommor, som har två blad var. Alltså 12 blad tillsammans.
I rabatten finns det 32 blad allt som allt. 32 – 12 = 20 blad som måste sitta på de växter som har skott. Växter med skott har fyra blad var. 20/4 = 5. Alltså finns det fem skott i rabatten.
(En liknande lösning kom från Daniel.)
Alicia i Örebro samt David i Angered använder bilder, ord och beräkningar.


Lösning på problem 3
Svar: Ja, minst en klarar sig. (Minst två blir träffade.)
Västernfilmer tar vi med en nypa salt men den som i verkligheten har sett människor skjuta på varandra, vill helst inte tänka på det. Douglas tycker att man skulle kunna göra lika bra problem om myror som sprutar syra på varandra. Brukar myror bete sig så? Om vi kommer överens att en cowboy blir träffad så snart han får ett kulhål i sin skinnjacka, så kan historien bli helt oblodig. Å andra sidan, beväpnade män som är rädda för varandra och ny teknik som spelar spratt, behöver diskuteras.
Många har svarat. Nästan alla svarar ”ja” som är det rätta svaret och många ger korta förklarningar som vittnar om äkta tankearbete:
• Det finns inga alternativa scenarior då alla cowboys dör, och alltså måste en cowboy överleva.
• Ja. En cowboy klarar sig alltid för den skjuter men ingen skjuter tillbaka.
• Ja, någon klarade sig för alla sitter inte närmast honom.
• En klarar sig.
• Ja, en klarar sig. För om den första skjuter den närmaste så dör den, sedan gör alla lika och då dör alla förutom den första.
• Det är en som överlever för de ska skjuta dem som är närmast.
• Ingen klarar sig.
• Ja, den som sitter längst bak.
Daniels förklarning:
”Eftersom alla cowboys sitter på olika avstånd måste det finnas en person som har det största avståndet till någon annan. Då kommer varje annan cowboy att inte träffa den cowboyen eftersom det alltid finns någon annan som sitter närmare. Därmed klarar sig den mest isolerade cowboyen helskinnad.”
Felet i detta resonemang är att det inte behöver finnas någon som ensamt har det största avståndet. Ett avstånd mäter man mellan två. Avstånden från A till G och från G till A är ett och samma avstånd.

A:s och G:s avstånd till den som är närmast är lika stor, det är avståndet mellan A och G. A och G är lika isolerade. I en sådan konfiguration skulle A skjuta mot G och G mot A.
Låt oss kalla ett par som skjuter mot varandra duellanter. Duellanternas antal, hur många dueller de än utkämpar, måste vara jämnt. Antalet cowboys är sju, ett udda tal. Alltså finns det någon eller några som inte är duellanter. Två i en duell skjuter lika långa skott medan de som inte är duellanter skjuter olika långa skott.
Vi modifierar Daniels förklarning:
Den bland ickeduellanterna, säg John, som skjuter det längsta skottet och träffar Bill, klarar sig därför att:
1. Ingen av duellanterna skjuter mot John, duellanterna skjuter bara mot varandra.
2. Ickeduellanterna (utom John själv) sitter minst lika långt eller längre från John än Bill gör, men de skjuter kortare skott än John, så inget av dem når honom.
En dag diskuterade Månadens problems redaktör cowboyproblemet med sina vänner. De var ense att om antalet cowboys skulle vara ett jämnt tal (t ex åtta i stället för sju), så skulle alla kunna bli skjutna. De skulle kunna sitta parvis så här
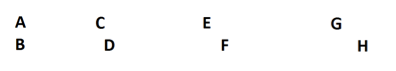
och utkämpa fyra dueller.
Om antalet är ett udda tal större än ett måste minst en klara sig, ansåg de, men ingen kunde bevisa det.
Nästa dag mötte vi Jakob som är fil dr i matematik. Han bevisade det på två sätt, med ett motsägelsebevis som använder permutationer samt med ett induktionsbevis. Alltså han bevisade att:
Om antalet cowboys är 2 ∙ n + 1, där n är ett positivt heltal så klarar sig minst en cowboy.
Men först formulerade han en hjälpsats:
Minst en cowboy klarar sig om och endast om en annan träffas av fler än ett skott.
Eftersom det skjuts lika många skott som det finns cowboys och varje skott träffar exakt en cowboy, så är det klart att hjälpsatsen gäller.
• Ett motsägelsebevis med permutationer.
Anta att ingen klarar sig. Enligt hjälpsatsen träffas varje cowboy av exakt ett skott. Det betyder att avbildningen som tilldelar varje cowboy den som han skjuter mot är en permutation. En permutation består av cykler. Summan av cyklernas längder är ett udda tal lika med antalet cowboys, alltså minst en av cyklerna måste ha en udda längd. Den är mer än ett eftersom ingen skjuter mot sig själv, alltså minst tre. Låt Jack vara den i en udda cykel som skjuter det kortaste skottet, han träffar Doc. Doc skjuter inte mot Jack eftersom då skulle cykellängden vara två. Doc skjuter mot den som sitter närmast honom, närmare än Jack. Alltså skjuter Doc ett skott som är kortare än Jacks, kortare än det kortaste? – en motsägelse.
• Ett induktionsbevis
Om n = 1 så det finns det tre cowboys. Två av dessa tre, de som sitter närmast varandra skjuter mot varandra. Den tredje klarar sig.
Anta att påståendet är sant för ett visst tal k när n = k alltså är antalet cowboys 2 ∙ k + 1. Vi ska visa att i så fall är det sant även när n = k + 1 alltså när antalet cowboys är 2 ∙ k + 3.
De två som sitter närmast varandra, säg Jesse och Joe skjuter mot varandra och inte mot någon annan (de utkämpar en duell). Om någon av de övriga skjuter mot en av dessa två så träffas han av två skott och då enligt hjälpsatsen gäller tesen. Om ingen av de övriga skjuter mot Jesse eller Joe, så uppfyller de övriga 2 ∙ k + 1 stycken påståendets premisser, alltså klarar sig minst en av dem enligt induktionsantagandet.
Innehåll: LR
