- Vi tackar:
Ina A samt Ebba och Hanna från Båstad Montessori, Asken
Daniel E Hvitfeldtska gymnasiet Matematikspets år 3
Mattegruppen på Käppala skola: Emma, Oscar, Matilda, Alexandra, Felix, Edvin, Sebastian och Jesper (Lärare: Jessica John)
Sonja och Emelie samt Alessandro och Reza 5A i Stora Högaskolan, Stenungsunds kommun (Lärare: Sara Hultberg)
Axel P, Lucas F och Kristian M åk 5 Malsta skola, Hudiksvalls kommun
David M i 3A, Långmosseskolan, Angered och Davids mamma

Lösning på problem 1
Svar: 2 bokstäver: M och E
Flera har förtydligat svaret med bild:
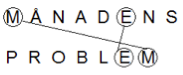
De två bokstäver som förekommer i båda orden hittar man kanske innan man börjar tänka, men för att bli säker på att det inte finns fler sådana par krävs eftertanke och noggrannhet.
Alessandro och Reza gjorde en tabell. För varje bokstav i ordet ”MÅNADENS” räknade de hur många gånger den förekommer i ordet ”PROBLEM”.
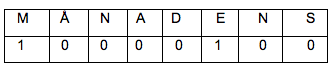
M och E förekommer en gång var. De andra bokstäver, inte alls.
Försök komma ihåg hur du undersökte det. Beskriv det för andra. Har alla gjort på samma sätt? Det finns fler sätt att göra det än man skulle tro.
Vi vänder på vår fråga:
Hur många av bokstäverna i ordet PROBLEM finns också i ordet MÅNADENS?
Självklart blir det samma svar här trots att det inte är precis samma fråga och man kanske skulle gå tillväga på ett lite annat sätt för att besvara den.
Att söka efter ett ord i hela internet eller att jämföra genetiska koder är i grunden samma sorts problem som detta, men mycket svårare, här krävs det verkligen planering. Till och med de kraftfullaste datorer måste använda väl genomtänkta metoder för att klara det.

Lösning på problem 2
Svar: 2
Det minsta sexsiffriga palindromtalet är 100 001 och det största femsiffriga 99 999. Så differensen är 2. Så enkelt är det. Det enda talet mellan dessa två är 100 000.
Elever i Malsta skola försökte krångla till det. De skriver att 000 000 är det minsta sexsiffriga palindromtalet. Så är det inte: vi säger att talet 0 är ett ensiffrigt tal därför att det kan skrivas med en siffra. ”000 000” är en sexsiffrig representation av samma ensiffriga tal.
En lite svårare fråga om palindromtal är: Vilka palindromtal finns det flest av, femsiffriga eller sexsiffriga? (Svaret efter problem 3)

Lösning på problem 3
Svar: 2x2 – P∙x + 2∙A
Det finns även andra polynom med samma två nollställen.
Nollställen till en funktion är de punkter i funktionens definitionsmängd för vilka funktionen antar värde 0. Med nollställen till ett polynom menas nollställen till motsvarande polynomfunktion. Rötter till ekvationen Q(x) = 0 är nollställen till funktionen Q(x).
Det kom lösningar från Daniel E samt från Davids mamma.
Daniel söker polynom av formen x2 + ax + b och använder sig av formler x1 + x2 = –a och x1 ∙ x2 = b där x1 och x2 är polynomets nollställen. Dessa formler blev härledda och beskrivna av den franske matematikern och astronomen François Viète på 1500-talet.
L ∙ B = A och 2L + 2B = P där L är längd och B bredd och när L och B är nollställen till x2 + ax + b dvs L = x1 och B = x2, så 2x1 + 2x2 = P och x1 ∙ x2 = A, alltså a = –P/2 och b = A vilket ger polynomet x2 – P/2 ∙ x + A.
Davids mamma, använde inga färdiga formler, utan tänkte ungefär som Viète tänkte.
L är ett nollställe till x – L och B till x – B, alltså både L och B är nollställen till (x – L)(x – B) eller mera allmänt nollställen till c(x – L)(x – B) där c är ett godtyckligt tal men helst inte 0 (vi vill ha ett polynom med bara dessa två nollställen och inga fler).
c(x-L)(x-B) = c∙(x2 – (L+B) ∙ x + L ∙ B) = c∙(x2 – P/2 ∙ x + A) och om vi väljer c = 2 får vi polynomen 2∙x2 – P ∙ x + 2 ∙ A.
Anm 1: Alla polynom av grad 2 med nollställen L och B har formen c∙(x2 – P/2 ∙ x + A) men det finns även polynom av högre grad som har samma mängd av nollställen.
Anm 2: Även ett rätblock med måtten L × B × H har polynom med nollställen L, B och H, t ex 4x3 – Px2 + 2Ax – 4V där P, A och V står för kanternas sammanlagda längd, blockets begränsnings area och blockets volym.
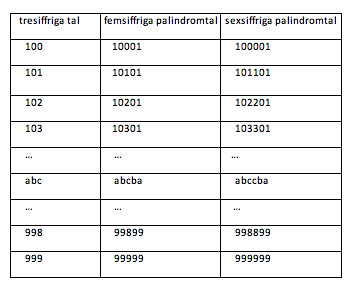
Svar till extrafrågan till problem 2: De är 900 av varje sort, lika många som alla tresiffriga tal. Det inser man när man betraktar följande tabell:
Innehåll: LR
