Svar och lösningar, januari 2016

Lösning på problem 1

Svar: Karl fyllde år på en tisdag.

Flera resonerar så här: Om imorgon är en torsdag så är idag en onsdag och då var igår en tisdag.

David visar det i ett diagram:

Även Samantha försöker visa det grafiskt med två pekare från onsdag-idag till torsdag-imorgon och till tisdag-igår.

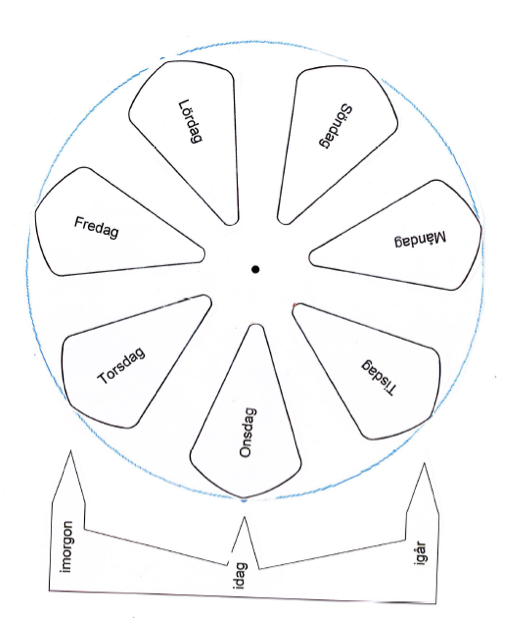
Vi har utvecklat vidare Davids idé och konstruerat en veckoklocka.

Klipp ut den runda veckoskivan och igår–idag–imorgon–pekaren! Pryda gärna med egna bilder eller klistermärken, eller skriv ett veckoschema eller en veckomeny. Veckoskivan ska klistras på en lika stor skiva av kartong och plastas in om den ska snurra i många veckor. Fäst skivan med en nål i mitten (i navet) på t ex en anslagstavla. Sätt fast pekarna till vänster om skivan. Veckoklockan har inget batteri, man får vrida den dagligen en sjundedels varv moturs för hand. Det går bra att klistra fästisar på veckoklockan för att minnas vad man har planerat att göra sju dagar framåt.

Lösning på problem 2

Svar: 170 cm

Flera kom till svaret genom att rita rektangeln, gissa sidolängder på de små rektanglarna och beräkna omkretsen på den stora. Nästan alla kom till rätt svar men det var den lätta delen av lösningen. Ni har visat att omkretsen av den stora rektangeln kan vara 170 cm, t ex:

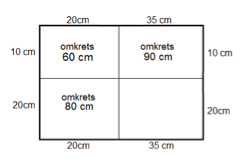
De små rektanglarnas omkrets stämmer och den stora är 170 cm, men blir det alltid samma resultat oavsett hur man gissar?

David tror sig ha löst problemet på två sätt: ett sätt som ovan och ett som följer, men det är först tillsammans som dessa två sätt bildar en fullständig lösning.

Douglas antyder ett bevis av att svaret måste vara 170:

“Man kan ta diagonalerna på omkrets, typ 90 + 80 = 170.”

Något ligger i detta. Omkretsen av den stora rektangeln är summan av omkretsar på två av de små rektanglarna, två som är diagonala mot varandra (dvs varken bredvid eller ovanför varandra).

David förklarar det tydligare och det som följer är ungefär som Davids andra sätt.

Tänk att du har åtta stickor, som bildar två av de små rektanglarna, en med omkrets 80 cm och en med omkrets 90 cm.

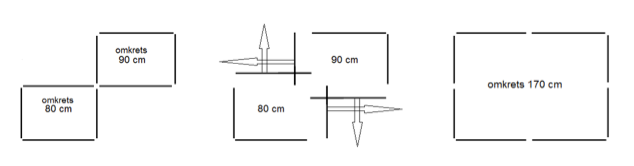
Förflytta de fyra stickor från mitten parallellt i pilarnas riktning tills de bildar den stora rektangeln. Alla åtta stickornas sammanlagda längd blir oförändrad: 80 cm + 90 cm = 170 cm.

Davids mamma påpekar att summan av omkretsarna av de två andra små rektanglarna också är lika med omkretsen av den stora rektangeln. Alltså vi kan beräkna att den fjärde lilla rektangeln måste ha omkrets 170 cm – 60 cm = 110 cm.

En ny fråga, egentligen tre frågor. Vilka omkretsar har följande tre rektanglar?

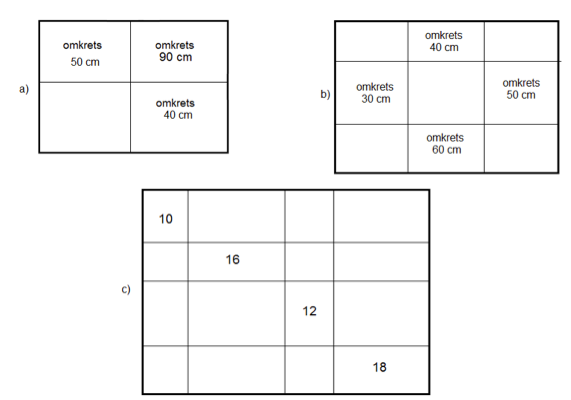
Lösningar och svar:

a) Omöjligt, det finns ingen sådan rektangel. Två diagonala rektanglar har 90 cm sammanlagt (40 cm + 50 cm), så hela rektangeln skulle ha 90 cm i omkrets. Då måste varje liten rektangel vara mindre än 90 cm i omkrets.

b) Går inte att bestämma exakt. Mera än 90 cm men mindre än 180 cm.

c) Det finns fyra små rektanglar “på diagonalen”. Vi kan resonera som i det ursprungliga problemet och visa att den stora rektangelns omkrets är summan av dessa fyras omkretsar: 10 + 16 + 12 + 18 = 56.

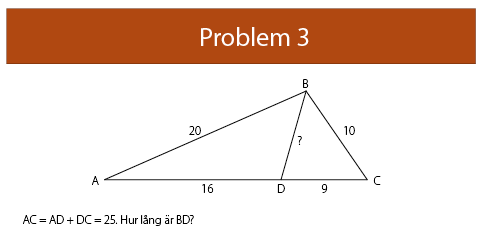
Lösning på problem 3

Svar: 8

Amanda K skriver: Man kan räkna ut den praktiskt om man är noggrann eller använda likformighet och få fram 10/x = 25/20, x = 10 ∙ 20/25 = 8.

Ja, Amanda har skickat oss en noggrann ritning med längdenheten 1 cm och BD är 8 cm på den. Det klarar man när man går i nian. Den teoretiska lösningen ser ännu enklare ut men inte många, inte ens de som har läst matematik på universitet, upptäcker att trianglarna ABC och ADB är likformiga. Ser man det så behöver man inte räkna mer än vad Amanda har gjort.

Alf Gunnarsson förklarar det närmare:

Sträckan BD kan beräknas med hjälp av cosinussatsen, men ett enklare sätt är att använda likformighet.

I den här uppgiften är vinkeln mellan de två största sidorna i trianglarna ABC och ABD gemensam.

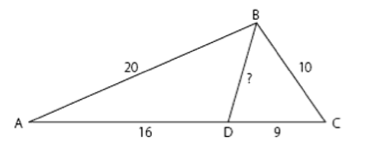
Förhållandet mellan de två största sidorna i respektive triangel är lika stort.

AB/AD = 20/16 = 5/4 och AC/AB = 25/20 = 5/4

Då är trianglarna ADB och ABC likformiga.

Likformighet ger:

BD/10 = 20/25

BD = 8

Skulle man byta ut någon siffra i figuren i problemet, så skulle inte trianglarna vara likformiga längre. Det finns allmänna metoder att lösa liknande problem oberoende om trianglarna är likformiga eller inte. (Amandas praktiska metod var en sådan men vi är ute efter teoretiska metoder.) Cosinussatsen som Alf nämnde har Anna S tillämpat. Den är ett effektivt verktyg för att klara liknande problem. Den lär man sig på gymnasiet. Den som kan cosinussatsen kan lösa problemet på tre sätt:

1. Från triangeln ABC beräkna cos(A) och använda den i triangeln ABD.

2. Från triangeln ABC beräkna cos(C) och använda den i triangeln BCD.

3. Utnyttja att cos(ADB)=-cos(CDB) och ställa upp två ekvationer och lösa dem.

Davids mamma använder Pytagoras sats och en del algebra men ingen cosinussats. Vi har delat upp hennes metod i två steg och kopplar beräkningar till figuren. Vi använder Pytagoras sats (flera gånger) samt konjugatregeln: a² – b² = (a + b) ∙ (a – b).

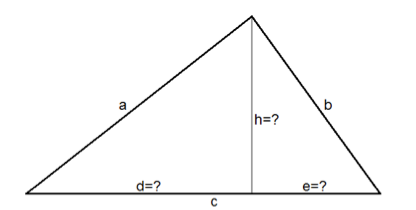
I en triangel med sidolängder a, b och c har vi dragit en höjd mot c och vill veta d, e och h.

a² = d² + h² och b² = e² + h²

a² – b² = d² – e² = (d + e) ∙ (d – e) = c ∙ (d – e)

d – e = (a² – b²)/c

När vi vet värden av d + e och d – e beräknar d och e:

d= ((d + e) + (d – e))/2

e= ((d + e) – (d – e))/2

sedan kan vi beräkna h med hjälp av Pythagoras sats.

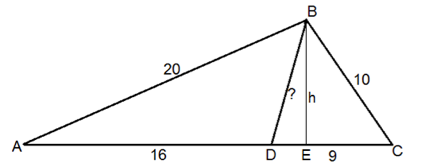
I problemets triangel har vi då a = 20, b = 10, c = 25

AE–CE =(20²–10²)/25 = 12

AE = (25 + 12)/2 = 18,5

CE = (25 – 12)/2 = 6,5

DE = 9 – 6,5 = 2,5

h² = 102 – 6,52 = 100 – 42,25 = 57,75

BD² = h² + 2,52 = 57,75 + 6,25 = 64

BD = 8

Innehåll: LR