- Oscar G, elev, (2003)
Wiggo A, åk 5, Vedums skola
Filip B.
David M, elev i 3A, Långmosseskolan, Angered och Davids mamma
Daniel E, elev på Hvitfeldtska gymnasiet (spetsutbildning i matematik åk 3)
Max D, åk 6, Kulparkskolan, Lund (lärare: Camilla Nejdesjö)
Jennie, Mohammed H, Sandra F, Dalia, Erik R, Sebbe, Filip P, Amanda, Besian, Nora K, Viktor, Elin och Isabelle E, 9b, Dalaskolan Södra, Bromölla
Douglas O, Båstad, Montessoriskolan
Maher Albedewi, studiehandledare på Tjärnaskolan i Borlänge

Lösning på problem 1
Svar: 27 och 34
Det första tvåsiffriga talet är 10, det andra 11, det tredje 12, det fjärde 13 och det femte 14.
Alltså, summan av det fjärde och det femte tvåsiffriga talet är 13 + 14 som är 27.
För alla tvåsiffriga tal gäller att talets värde är 9 mer än dess ordningsnummer bland de tvåsiffriga talen,
så det tolfte är 12 + 9 = 21, det trettonde 22 och deras summa, 43 har ordningsnummer 43 – 9 = 34.
De flesta som har beskrivit hur de räknade, har använt uppräkning för de mindre talen och differensen 9 för de större.
David och Nora förklarar varför tvåsiffriga talens värden är 9 större än deras ordningsnummer.
Räknar man från 1 och uppåt så är talens värden lika med deras ordningsnummer.
När vi räknar bara de tvåsiffriga talen, hoppar vi över de 9 ensiffriga talen 1 till 9.

Lösning på problem 2
Svar: 35 m2
De flesta har gett exempel på rektanglarnas möjliga sidolängder:
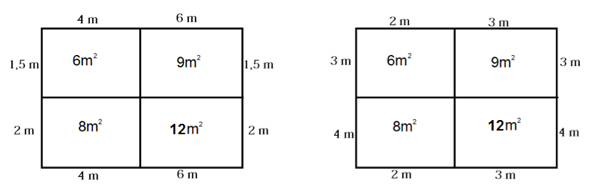
Man ser att de tre givna areorna av rektanglar stämmer. Den fjärde rektangeln är 6 m ∙ 2 m eller 3 m ∙ 4 m och har arean 12 m2. Så den hela stora rektangeln har, i exemplen, arean 6 m2 + 9 m2 + 8 m2 + 12 m2 = 35 m2.
Sandra drar slutsatsen att: ”Den stora rektangeln kan ha arean 35 m2.” Längderna i figurerna är gissningar. Det går inte att bestämma dem från de givna premisserna.
Flera andra påstår att ”rektangeln har arean 35 m2”. Det är sant oberoende av gissningar, men bara Daniel bevisar det.
Daniels lösning:
Kvoten mellan arean av de rektanglarna i den översta raden är 9/6 = 3/2. Eftersom de har en lodrät sida gemensam, är denna kvot även kvoten av rektanglarnas vågräta sidor. Denna kvot kommer då vara lika stor som kvoten mellan rektanglarnas areor i den nedersta raden, då deras vågräta sidor förhåller sig på samma sätt och de också har en lodrät sida gemensam. Arean av den okända rektangeln blir då 8 · (3/2) = 12. Totala arean av den stora rektangeln är därmed 6 + 9 + 8 + 12 = 35.
Kanske var det flera som tänkte som Daniel men det gäller också att förklara hur man tänker.

Lösning på problem 3
Svar: Den fjärde triangelns area måste vara en av 9 cm2, 16 cm2 eller 25 cm2.
Nora och Elin kom fram till att fyrhörningen inte kan vara en rektangel (i synnerhet inte en kvadrat). Rektangelns diagonaler delar den i fyra trianglar med lika stora areor. (Detta gäller inte bara rektanglar utan alla parallellogram.) Så småningom hittar Nora en sådan fyrhörning:
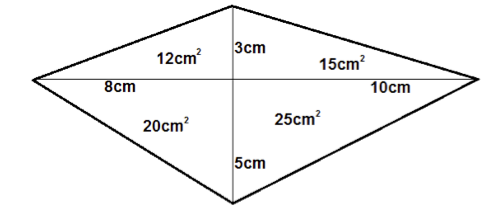
Den delas i fyra rätvinkliga trianglar. Tre av dem har areor 12, 15 och 20 cm2. Den fjärde är 25 cm2. Och Nora svarar: ”Arean på den fjärde triangeln kan vara 25 cm2.” – lika klokt och försiktigt som Sandra i problem 2.
Max har ritat en fyrhörning med lite annorlunda mått men diagonalerna delar fyrhörningen i fyra rätvinkliga trianglar med samma areor som ovan. Hans konklusion är: ”Nej, den kan inte vara hur stor eller hur liten som helst för måtten kan inte vara hur stora eller hur små som helst.” – Det var ett djärvt försök men fel. Det finns fyrhörningar som kan ha både mycket korta och mycket långa sidor samt mycket korta och mycket långa diagonaler men ändå uppfyller premisserna.
Davids mamma samt Daniel har använt formler för triangelns area för att bevisa ett intressant samband mellan de fyra trianglarnas areor. Det var formeln: area = basen ∙ höjden / 2.
I en alternativ lösning använder Daniel också den så kallade areasatsen, men här presenteras bara den första metoden.
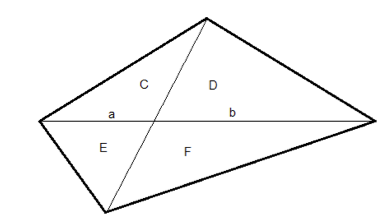
Diagonalerna delar en fyrhörning i fyra trianglar med areorna C, D, E och F. Vi ska också benämna trianglarna som C, D, E och F. Den vågräta diagonalen delas i två avsnitt: a och b. Trianglarna C och D har samma höjd mot den vågräta diagonalen, säg h. Då har vi C = a ∙ h / 2 och D = b ∙ h / 2. Alltså C : D = (a ∙ h / 2) : (b ∙ h / 2) a : b.
På samma sätt får vi E : F = a : b. Alltså C : D = E : F och av detta följer C ∙ F = D ∙ E.
Med hjälp av den sista likheten kan vi beräkna arean av en av trianglarna när vi vet de övriga tre trianglarnas areor: C= D ∙ E / F, D = C ∙ F / E, E = C ∙ F / D och F = D ∙ E / C eller med ord: En triangels area är produkten av de intilliggande trianglarnas areor delad med den motstående triangelns area. Areor av tre av trianglarna är 12, 15 och 20 cm2, vi vet inte vilken av trianglarna är den motstående till den okända triangeln. Därför finns det tre möjligheter 12 ∙ 15 / 20 = 9, 12 ∙ 20 / 15 = 16 och 20 ∙ 15 / 12 = 25.
Det är lätt att konstruera exempel för att visa att alla tre är geometriskt möjliga.
Daniel anmärker att alla tre svar är heltalskvadrater.
Det är inte slumpen, det finns inget i geometrin eller i algebran som orsakar detta men det har ett samband med heltalens egenskaper.
Innehåll: LR
