- Höstens första lösningar kom från:
Wilma Z, Tilde I, Lucas E, Colin A och Melvin Å i klass 1, Amelie, Nora V, Filippa M och Alma K i klass 2, Nora K i klass 2-3 samt Kelly A, Simon H, Wilma E, Jennifer S, Milon G och Alvin I i Örsjö skola, Nybro.
Otto och Douglas i Båstad Montessori Asken klass 4. (lärare: Johanna Roth)
Hugo i 8A och Selma i 9A i Rydsbergsskolan i Lerum. (lärare: Elinor Larsson)
Elsa som är en elev i nian.
Dalia, Elin P, Isabelle E, Amanda K, Nora K, Viktor A, Filip P, Samantha E, Besian K, Max F och Mohamed H i 9B i Dalaskolan Södra, Bromölla.
Leon och Sabina i 4C samt Axel och Anton i 4A samt Andrija i Grönkullaskolan i Alvesta. (Viktoria Lundström, specialpedagog)
Wilma L i 7D Henån.
Musdalifo, Nura, Jasmin, Ida, Emmie, Dulijano, Ajla, Selma, Amanda, Johanna, Maksymilian, Redon, Sam och Siri i klass 2a i Grönkullaskolan (lärare: Pernilla Karlsson Nordin)
David M (med sin mamma), elev i 3A, Långmosseskolan, Angered.
Leonard L och Alex J klass 6C Korpadalsskolan (lärare: Margareta)
Edwin och andra i Grossbolsskolans 3-4 Lila, Forshaga kommun (lärare: Mari Lindström)
27 barn i årskurs 1 i Sjötorpsskolan, Huddinge (lärare: Ágnes Végh Blidlöv)

Lösning på problem 1
Svar: Tre barn gömmer sig fortfarande.
Det var 13 barn, Hektor som stod och 12 barn som gömde sig. Han hittade nio och i så fall finns det tre barn (12 – 9 = 3) som fortfarande gömmer sig.
Många tyckte att det var ett mycket lätt problem men det är också lätt att glömma Hektor och bara räkna 13 – 9 = … Då får man fel svar.
Många har också ritat bilder och alla som har gjort det har svarat rätt.
Maksymilian, Redon, Sam och Siri skriver:
När det är en som letar så är det 12 barn som man ska hitta.
Först hittade han nio barn sen är det tre kvar att hitta.
1 + 12 = 13, 9 + 3 = 12, 1 + 9 + 3 = 13

Lösning på problem 2
Svar: 20 cm
Vi ser på bilderna att rektangelns sidor också är kvartscirklarnas radier. Vet man en cirkels radie kan man beräkna dess omkrets. Längden på kvartscirkelns båge är en fjärdedel av cirkelns omkrets och våra figurers ränder består av sådana kvartscirkelbågar och rektangelns sidor. Vi lägger samman längderna på varje omkrets delar och sedan beräknar vi differensen. Många har gjort så och fått rätt svar.
Kan man inte beräkna det ännu enklare?
David ritade av bilderna och kopplade samman delar av randen på ena bilden med lika långa delar av den andra bildens rand. Det blev tre raka avsnitt på den vänstra bilden kvar som inte hittade sina par i den högra bilden, en 10 cm lång och två 5 cm långa. Så han behövde inte räkna mycket: 10 cm + 5 cm + 5 cm = 20 cm.
Hugo, som räknar likadant, förklarar det så här:
”De böjda sidorna behöver man inte kunna räkna ut för båda figurerna har samma böjda sidor.” Sedan använder han ett algebraiskt skrivsätt: kallar den sammanlagda längden på ”de böjda sidorna”, (bågarna) i en figur för x, de är lika långa i den andra figuren så även här får de heta x, och skriver formler för figurernas omkretsar:
Figur 1: O1 = 10 cm + 10 cm + 5 cm + 5 cm + x = 30 cm + x
Figur 2: O2 = 10 cm + x
Differensen: O1 – O2 = (30 cm + x) – (10 cm + x) = 20 cm
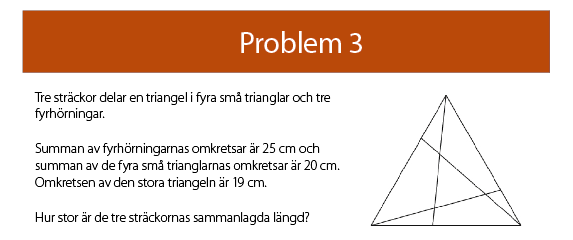
Lösning på problem 3
Svar: 13 cm
Många har löst även Problem 3 den här gången.
En sådan här bild av den stora svarta triangeln uppdelad med blå linjer i små trianglar (röda) och fyrkanter (gula) har David skickat.
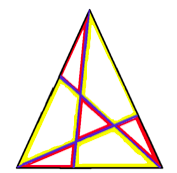
Kanske med lite hjälp från sin mamma har han ritat en lika fin bild som Amanda K och andra flickor i årskurs 8 i Dala skolan. Ser man figuren så kan man skriva följande färgekvation:

Den kan läsas: Om man tar bort de gula och röda linjerna som går längs den svarta linjen så blir de linjer som går på båda sidor av de blå linjerna kvar.
När David sedan ersatte färger med respektive linjers längder, de som var kända, fick han en mera vanlig ekvation:
25 + 20 – 19 = 2 · blå.
Av detta kan utläsas att blå är 13.
Selma i Rydsbergsskolan för ett resonemang som är kortare än andras: Hon märker att de sju områdenas ränder (spelar ingen roll vilken form de har) går två gånger längs varje avsnitt av de linjer som delar triangeln och ett varv runt själva triangeln. Sedan räknar hon 25 + 20 – 19 = 26 och 26/2 = 13. Flera har räknat så, men utan en förklaring.
Tänker man mer generellt, kan man säga att triangeln och de tre ”blå” linjerna delar hela planet i åtta delar. Omkretsen av alla dessa delar är sammanlagt dubbelt så lång som de delande linjernas sammanlagda längd. Man får då ekvationen
25 cm + 20 cm + 19 cm = 2 · (19 cm + x)
där x är längden av de ”blå” linjerna och 19 cm är egentligen inte triangelns omkrets utan omkretsen av planet med ett triangulärt hål. Sedan är det enkelt att ur ekvationen bryta ut x och beräkna att x = 13.
Man skulle kunna tro att planets (med eller utan hål) omkrets är oändlig men ett områdes omkrets är längden av den linje som avskiljer området från de övriga och där i oändligheten finns det ingenting som planet behöver avskiljas ifrån.
Innehåll: LR
