- Lösningar har kommit från:
4A & 4B på Käppala skola, Lidingö (lärare: Jessica John)
Jermy, Leo och Ludvig, Linnéa och Philip samt Katarina och Märtha i åk 2 i Fredrikshovs slotts skola, Stockholm (Lärare: Karolina Dahlberg)
Sture S
Wiggo A i åk 4 på Vedum skola, Vara
Lösning på problem 1
Svar: Om tre år.
Nu är Tore 13 år. För två år sedan var han 11.
Då var Tommy 4 år eftersom de tillsammans var 15.
Det har gått 2 år sen dess och Tommy är 6 år nu, så det dröjer 3 år till innan han blir 9.
Lösning på problem 2
Svar: Den gröna bläckfisken talar sanning.
Frågeformuleringen antyder att en av bläckfiskarna säger sanning men det framgår även på annat sätt: säger inte den blåa sanning, så har inte de fyra bläckfiskarna 28 armar tillsammans. Alltså har minst en annat än 7 armar och den talar sanning.
Vilken, den som talar sanning än är, så måste de övriga tre ljuga eftersom de alla påstår olika saker. Dessa tre har 7 armar var, den som talar sanning har 6 eller 8, det blir 27 eller 29 sammanlagt.
Den gröna säger 27, det som de övriga 3 säger kan inte vara sant. Den gröna bläckfisken är den som talar sanning.
Lösning på problem 3
Svar: 6.
Vi ska använda följande två påståenden:
A: Mittpunkten på hypotenusan av en rätvinklig triangel har lika stora avstånd till triangelns alla hörn, t ex:
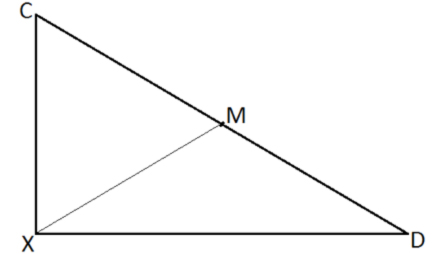
Om CXD = 90° och CM = MD så XM = CM
B: Längden av en rät linje som förbinder mittpunkterna på axlarna av en parallelltrapets är medellängden av parallelltrapetsets baser, t ex
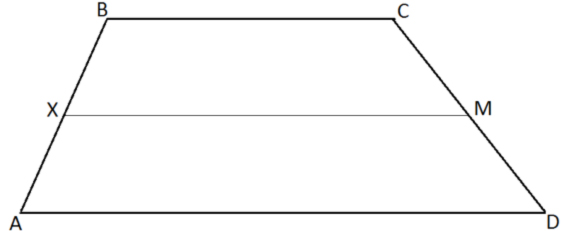
Om BC är parallell med AD och AX = XB och CM = MD så XM = (AD + BC)/2
Tre förslag på bevis av A:
1. Triangeln är hälften av en rektangel. M är skärningspunkten av rektangelns diagonaler.
2. Enligt omvändningen av randvinkelsatsen är M medelpunkten i den kring triangeln omskrivna cirkeln.
3. Placera triangeln i ett koordinatsystem med kateterna på var sin axel (och rätvinkeln i origo). Uttryck koordinater av hypotenusans mittpunkt mha hörnens koordinater.
Två förslag på bevis av B:
1. Om parallelltrapetsen ABCD är en parallellogram så är även BCXM det.
Använd annars transversalsatsen: Låt K vara skärningspunkten av parallelltrapetsens förlängda axlar. Bevisa att XM är parallell med AD. KB : BC = KX : XM = KA : AD.
2. Med vektorkalkyl:
Låt u = AX = XB och v = CM = MD.
u + XM + v = AD
u + BC + v = XM
AD + BC = u + XM + v + BC = XM + u + BC + v = XM + XM
Nu räknar vi omkretsen:
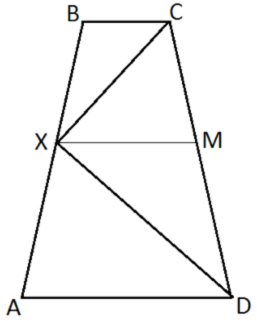
CDX är en rätvinklig triangel med hypotenusan CD. Låt M vara mittpunkten av CD.
Då gäller: MC = MX = MD
Eftersom trapetsen är likbent så gäller AB = CD. Alltså AX = XB = CM = MD = XM = 1.
Omkretsen är AX + XB + BC + CM + MD + DA = 1 + 1 + BC + 1 + 1 + DA = 4 + 2∙XM = 6.
Sture S har även undersökt trapetsens area. Den ligger mellan 2 och kvadratroten ur 3.
Innehåll: LR
