Lösningar av problem 1, 2 och 3 har kommit från:
- Linnéa, Ottilia, Julia och Tilda i 6:an på Hilllerstorpsskolan
- Anna Schastnaya, Klara Norra Gymnasium, Stockholm
- Ylva, Albin och Pianca i åk 7, Kunskapskolan i Uppsala (lärare: Emil Ohlander)
- Laura Wey, SU
- Vera P.
- Marcin W.
Det har också kommit flera svar på extraproblemet. Prisbeslutet kommer att kungöras inom kort

Svar: 14
När Martin kom halvvägs till Klara så hade han hälften av tolv, alltså sex, våningar kvar. Klara bor alltså sex våningar över den åttonde, dvs på fjortonde våningen.
Lustigt att nästan alla räknar först på vilken vånning Martin bor, för att sedan beräkna Klaras våning.
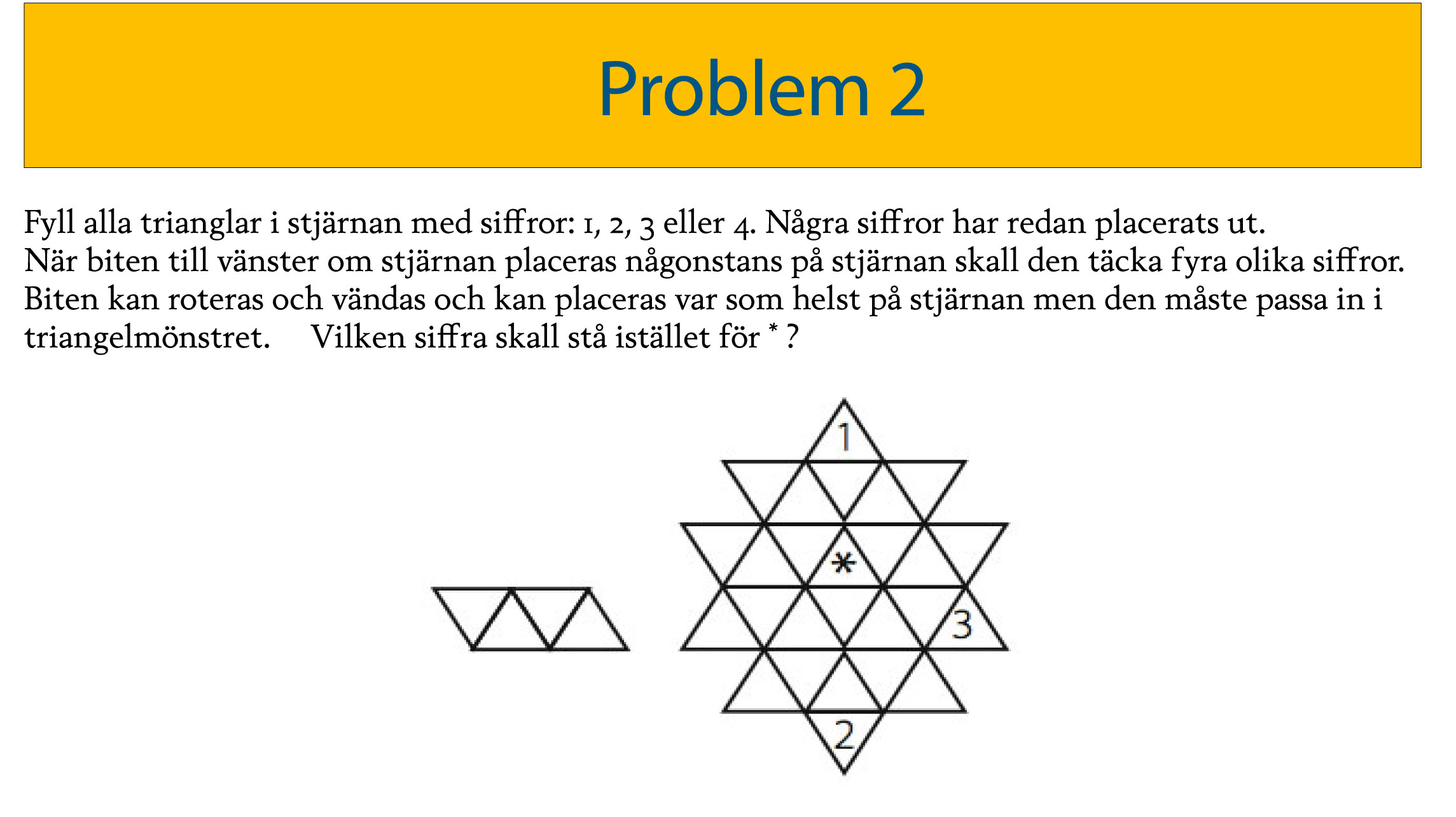
Svar: 2
Vrida, vända, rotera (och det finns fler ord) är ord som ofta kan betyda samma sak men ibland gör man skillnad. Om ett platt föremål ligger på ett bord, så kan man vrida eller rotera det genom att låta den glida på bordsytan eller också vända det genom att lyfta och lägga det på bordet igen med den tidigare osynliga undersidan upp. Ett annat sätt är att ställa en spegel bredvid föremålet. Då ser man det spegelvänt, man ser inte dess undersida och dess kontur blir som om man hade vänt den på det första sättet.
I vårt problem får man både rotera och/eller vända ”biten”, eller parallellogrammen.

Här till vänster ser vi fyra kopior av parallellogrammet efter rotationer, till höger spegelbilder av de förra. Man kan inte få den ursprungliga biten i läge av någon av de till höger bara genom att flytta och vrida den utan att lyfta den ur planet (bordsytan).
Efter några försök med blyerts och sudd hittar man ett sätt att fylla i stjärnan, ett sådant är att parallellogrammen alltid täcker fyra olika siffror. Man hittar det snabbast om man gissar så lite som möjligt, dvs i första hand fyller man i en siffra i en triangel där man kan utesluta de övriga siffrorna.
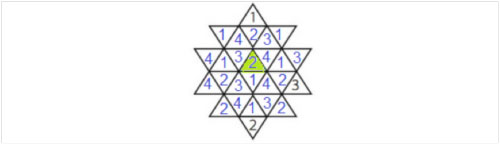
Observera att i varje rad, vågrätt eller snett, följer siffrorna ett mönster.
Man ser att i triangeln med asterisken (nu markerad med grönt) kan en tvåa stå. Men vi nöjer oss inte med att hitta ett möjligt sätt att fylla i stjärnan, vi ska också bevisa att det inte går att fylla den med en annan siffra än en tvåa i den markerade triangeln.
Fem trianglar i rad, som kan gå vågrätt eller snett, bildar en parallelltrapets.
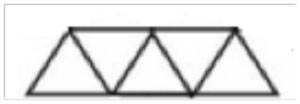
Två siffror i en sådan trapets måste vara lika eftersom vi bara får använda fyra olika siffror, men de första fyra (dvs alla utom den sista) och även de sista fyra (dvs alla utom den första) måsta vara olika. Alltså, de som ska vara lika måste vara den första och den sista, t ex:
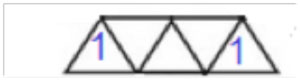 .
.
Tar vi tre sådana parallellogrammer, var och en med en ända i en redan ifylld triangel, så ser vi ytterligare tre trianglar där det måste stå en etta respektive tvåa och trea (se den vänstra stjärnan).
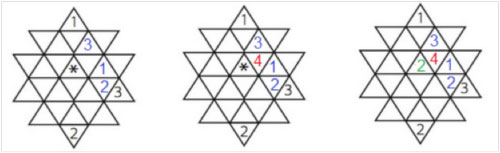
När vi har fyllt i dessa tre siffror, så ser vi en triangel där inget annat än en fyra passar (se den mittersta stjärnan). Fyller vi i den, så kan vi se att inget annat än en tvåa kan ersätta asterisken.
Anmärkningar:
Det är ganska lätt att se att hela stjärnan bara kan fyllas i på ett sätt när de tre första siffrorna är givna. Mycket svårare att bevisa, men som faktiskt är sant, är att samma skulle gälla även om man inte skulle få vända på parallellogrammen, (bara vrida). I ett bevis av detta använder man en sådan här figur:
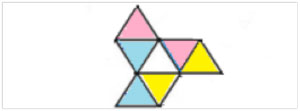
Lika siffror ska täckas med likafärgade trianglar.
Svar: 55°
Här är det tre saker som man behöver veta om trianglar:
• att vinkelsumman är 180°
• att sidor mittemot lika vinklar är lika långa
• att vinklar mittemot lika långa sidor är lika stora
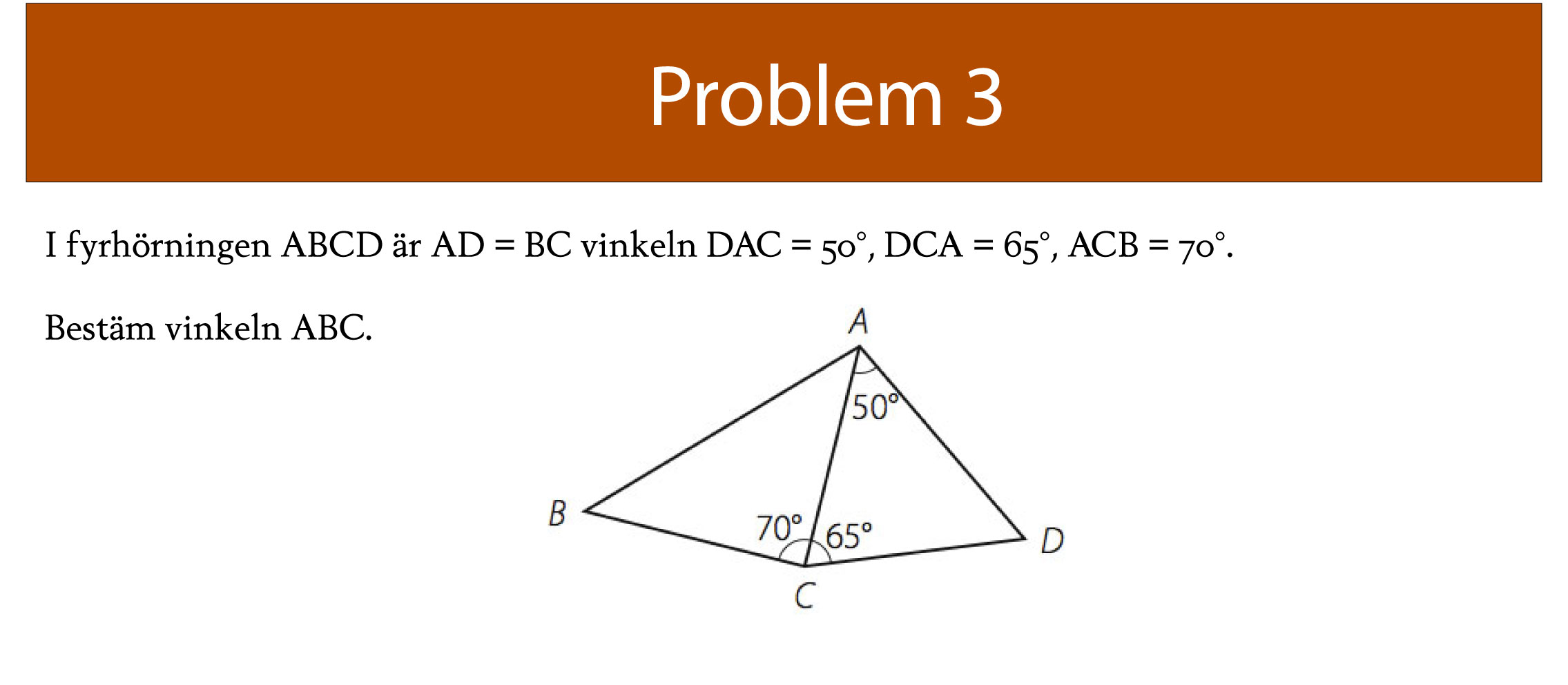
Då ∧ADC = 180°-50°-65°= 65° är alltså ∧ADC = ∧ACD. Alltså är AC = AD,
men AD= BC. Alltså är AC= BC och ∧ABC= ∧BAC = (180°-70°)/2 = 55°.
Innehåll: LR
