Det har kommit svar och kommentarer från:
- Hans H. i Motala
- Ellie H. på Sandsbro skola i Växjö
- Erik H. i Svedala
- Anna S. på Klara Norra Gymnasium
- Seidi C. från Motala
- Vera P. i klass 4a Lilla Adolf Fredriks skola i Stockholm)

Svar: De hade köpt mellan 6 och 10 par skor.
Ett sådant fullständigt svar ger Anna S. De var alltså 5 till 9 vänner. De flesta svarade 10. OK, det kunde vara 10 par skor. Vera svarar: Dom måste köpa minst sex par skor.
Undrar man vilka storlekar de hade köpt så finns det hela 55 möjliga svar. (55 tillhör Fibonaccis talföljd: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … och det är inte en slump.) Både Anna och Vera ger exempel på vilka storlekar de skulle kunna ha köpt och hur de i så fall fördelade dem mellan sig. Anna och Vera använder olika sätt att presentera sina lösningar: Båda använder tabeller med färger men på olika sätt.
Annas exempel med 6 par skor:
De flesta förutom en har 2 storlekars skillnad. Det ser ut så här (minsta antal 6 par för 5 kompisar):
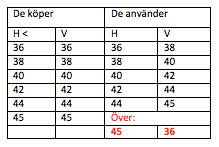
Annas exempel med 10 par skor:
Största antalet är 10 för 9 kompisar
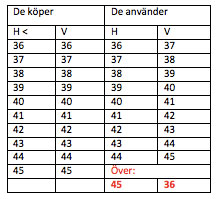
Veras exempel med 6 par skor:

(De röda siffrorna visar skorna som blir över när alla vänner har tagit sina skor och de svarta inte är köpta än)

Svar: 17.
Kroppen är en polyeder av en mera ovanlig sort, sådana kallas bipyramider. Om man tar två pyramider med likadana baser (egentligen spegelvända mot varandra) och limmar samman dem bas mot bas så får man en bipyramid. I vår bipyramid har den ena pyramiden spetsen uppåt och den andra pyramiden spetsen neråt. Pyramiderna har en gemensam triangulär bas, (triangeln på mellannivån).
Hjälpsats: Om en polyeder med ett tal i varje hörn har två triangulära sidoytor med en gemensam kant och summan av talen vid varje sidoyta är lika så måste de två ”fria” hörnen, de som inte ligger vid den gemensamma kanten, ha lika stora tal.
Bevis:
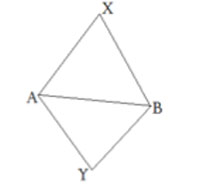
A+B+X=A+B+Y. Alltså är X=Y, vilket skulle bevisas.
Se nu på kroppen i vårt problem.
Enligt hjälpsatsen måste talet vid det nedersta hörnet vara samma tal som det på toppen, alltså 1. Även de övriga tre talen måste, enligt hjälpsatsen, vara lika sinsemellan, alltså 5. Summan av alla fem talen blir 1+1+5+5+5=17.
Veras lösning är så gott som identisk med den ovan men i stället för att formulera hjälpsatsen upprepar hon den algebraiska tankegången i hjälpsatsens bevis för varje nytt hörn. Även Hans och Anna löser problemet algebraiskt (med hjälp av ekvationer).
En fördel med hjälpsatsen är att man kan återanvända den när man vill undersöka andra kroppar med triangulära sidoytor som t ex tetraeder, oktaeder eller ikosaeder (som har 20 sådana sidoytor).

Svar: 9.
Här kommer flera lösningar:
Hans: 0,8,4,1,5,10,2,6,3,9. Det blev hela 10 tal! Men 0 måste strykas, det är inget positivt tal.
Erik: 9. Rätt svar.
Anna: Det var 9 tal: 9, 3, 6, 1, 5, 10, 2, 4, 8. Helt rätt.
Seidi: talen var 1 2 4 8 6 3 9 5 10 = 9 st tal. Stämmer, men det var inte i den ordnigen som Romeo skrev dem. 9 och 5 passar inte samman.
Vera: 9 tal. Det finns olika lösningar. Här kommer en av dem: 5 10 2 8 4 1 6 3 9. Helt rätt.
Inte i något av svaren ovan förekommer talet 7. Skulle man inte kunna pressa in det någonstans mellan de andra talen och få an följd med alla tio positiva heltal som är mindre än 11? Eller byta ut något av de övriga tal mot 7 och få en följd med nio tal men med sjuan bland dem?
För att få ett svar på detta, gör vi en översikt av par av tal som passar ihop. Alla tal är delbara med 1 och det finns fyra tal (utom tvåan själv) som är delbara med 2. Det blir många par men vi lägger 1 och 2 åt sidan och tittar på de övriga talen. Då ser det ut så här:
6 3 9 … 4 8 … 5 10 … 7
Endast talen som står bredvid varandra, utan punkter emellan passar ihop. Vi har alltså fyra kedjestumpar som vi får länka samman med hjälp av 1 och 2 till en lång kedja. Men med bara två länkar (1 och 2) kan vi inte länka samman fler än tre av dessa stumpar. För att få en kedja som är så lång som möjligt måste vi använda de tre längsta stumparna och avstå från den kortaste som består bara av sjuan. Därför får inte sjuan vara med.
Ellies svar: Ellie hade nog läst texten och missuppfattat förutsättningarna. Romeo skrev sina tal i en rad medan Ellie sorterar dem i par: 1 7 ; 2 6 ; 4 8 ; 3 9 och 5 10. Det var lättare att göra det än att ordna dem i en rad. Men å andra sidan är detta en lösning på ett annat intressant problem: Om vi har alla heltal från 1 till n, kan vi sortera dem alla i par så att det ena talet i varje par ska vara delare till det andra?
Talet n måste naturligtvis vara ett jämt tal för att det ska vara möjligt att sortera talen 1 till n i par. Vill vi dessutom att talen i varje par ska passa ihop enligt Romeo och Julias princip, så det visar sig att det är bara möjligt att göra på ett sätt om n är 2, 4, 6 eller 10 och är helt omöjligt för alla andra n.
Innehåll: LR
