Den här månaden har det kommit lösningar från Martina och Patricia i årskurs 8 och från Alice i 8a i Saltsjöbadens Samskola; från spec pedagog Hassan Salehian i Botkyrka; från 3beta och 3alfa i Kungsbacka (lärare: Christina Källqvist); från Ida och Oskar i 5F, Fryxellska skolan i Västerås samt från Vera i Lilla Adolf Fredrik skola i Stockholm.
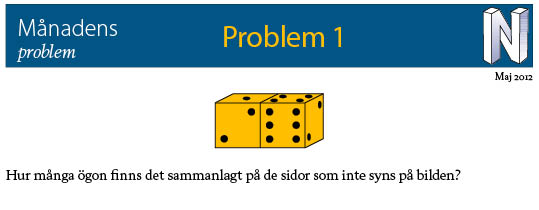
Svar: 27 ögon (eller prickar)
Här räknar man på lite olika sätt, beroende på vad man vet om tärningar.
Ida och Oskar visste att: ”Det finns alltid 7 st prickar mittemot varandra på en tärning.” För varje tärningssida som syns beräknade de antalet prickar på den osynliga sidan mittemot och lade till de 7 prickar (måste vara 3 och 4) som finns på den högra och den vänstra sidan av den vänstra tärningen (det par av motstående sidor, där ingen sida syns). De fick då fram att den högra tärningen har 1+5+3=9 osynliga prickar, den vänstra 5+6+4+3=18 och sammanlagt finns det 9+18=27 osynliga prickar.
Martina och Patricia och även Hassan visste att en tärning har sammanlagt 21 ögon på alla sidor. Då har två tärningar 42 ögon. De räknade bort de 15 ögon som syns och fick fram att det finns 27 osynliga ögon.
Om man inte vet, eller inte minns hur många ögon en tärning har, så kan man beräkna det så: 1+2+3+4+5+6=21 eller så som Vera gjorde: 3*7= 21 (3 par av motstående sidor med 7 ögon per par).
Alice räknade det totala antalet ögon på 2 tärningar på en gång:
2*1+2*2+2*3+2*4+2*5+2*6=42.
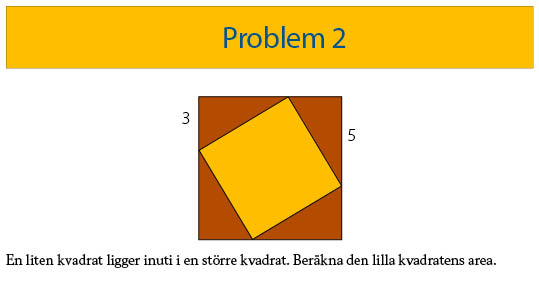
Svar: 34
Det är uppenbart att de fyra bruna rätvinkliga trianglarna är kongruenta (dvs lika till formen och till storleken). De har ju lika stora vinklar, därför att sidorna i varje triangel är alla parallella eller alla vinkelräta till motsvarande sidor i var och en av de övriga trianglarna. Och lika stora måste de vara, då alla deras hypotenusor är sidor i samma kvadrat.
Så här räknade Martina och Patricia:
Stora kvadratens sida = 3 + 5 = 8. Stora kvadratens area = 8 x 8 = 64.
Trianglarnas area: 3×5/2 = 7,5. Trianglarnas sammanlagda area: 7,5 x 4 = 30.
Lilla kvadratens area: 64-30 = 34. Likadant räknade Hassan, Alice och Vera.
I en alternativ lösning använder Vera Pytagoras sats. Den lilla kvadratens sidor är ju hypotenusor i rätvinkliga trianglar med kateter 3 och 5, så kvadratens area är kvadrat av hypotenusan som är lika med summan av kvadraterna på kateterna 3*3+5*5=9+25=34.
Nu tar vi en godtycklig rätvinklig triangel, den har kateter a och b och hypotenusan c. Av fyra kopior av den bildar vi en kvadrat med sidan a+b och med ett hål i form av en kvadrat med sidan c (den lilla kvadraten). Den stora kvadratens area är (a+ b)², hålets c². Men hålets area kan också bestämmas som den stora kvadratens area minus de fyra trianglarnas area.
c² = (a+ b)² – 4*ab/2 = a² + 2ab + b² – 2ab = a² + b² .
Vi har bevisat Pytagoras sats.
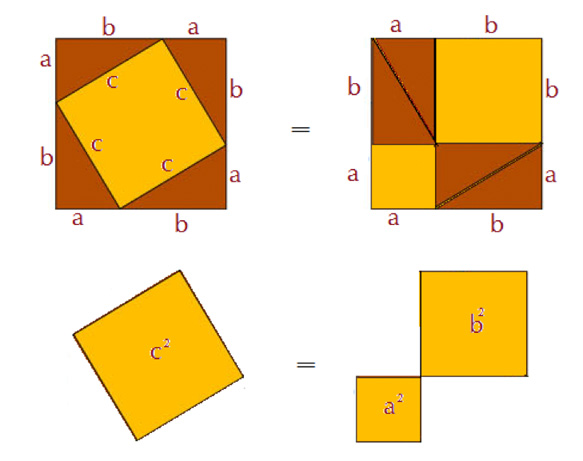
Detta är ett av de många sätt att bevisa Pytagoras sats som man har kommit på sedan tidernas begynnelse. (Observera att om vi hade använt Veras alternativlösning så skulle det inte bli något bevis, bara ett cirkelresonemang.)

Svar 5 meter. (Enheten, meter, var inte känd i antiken men kanske använde man alnar som var ungefär 1/2 m alltså 24 alnar långt rep med knutar 6 respektive 10 alnar från var sin repände. Hur som helst, det är inte längder utan proportioner mellan dem som är intressanta.)
Här gällde det att svara på frågan: Vilken hypotenusa har en rätvinklig triangel med omkretsen 12m och ena kateten 3m?
Alice antar att andra katetern är 4m, beräknar med hjälp av Pytagoras sats att hypotenusan i så fall är 5m och omkretsen 3m + 4m + 5m = 12m.
Martina och Patricia antar från början att triangelns sidor är 3, 4 och 5 och kontrollerar att 32 + 42 = 52. Här använder de egentligen den omvända satsen till Pytagoras sats (som också är en följdsats till Pytagoras sats) som säger att om sidor i en triangel har längder a, b och c och a² + b² = c², så är triangeln rätvinklig och sidan med längden c är hypotenusan.
Låt oss beteckna den kända kateten med a, den okända med b, hypotenusan med c och omkretsen med P. Vi vet att a = 3 och P = a + b + c = 12.
Ungefär så här resonerar Vera: En katet är a = 3 och omkretsen P = 12 så de två återstående sidor b + c är 9 tillsammans och hypotenusan c som är längst måste vara mera än 4,5 men varje sida i en triangel är kortare än halva omkretsen alltså 4, 5 < c < 6 alltså c = 5.
Veras resonemang visar att 5 är den enda heltalslängden som uppfyller problemets premisser. Men det kan överhuvudtaget inte finnas två rätvinkliga trianglar med en katet 3 och olika långa hypotenusor (heltal eller inte) och som har lika lång omkrets.
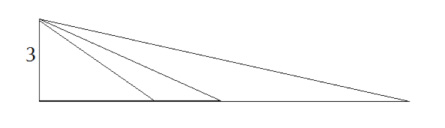
Ju längre hypotenusan desto längre omkrets. Alltså b måste vara 4.
Här kommer ett algebraiskt bevis på detta:
Anta att b < 4. Då är b² < 16 och c² = a² + b² = 9 + b² < 9+ 16 = 25, alltså c² < 25 och c < 5 och omkretsen P = a + b + c < 3 + 4 + 5 = 12, alltså P < 12.
Anta att b>4. Då är b² > 16 och c² = a² + b² = 9 + b² > 9+ 16 = 25, alltså c² > 25 och c > 5 och omkretsen P = a + b + c > 3 + 4 + 5 = 12, alltså P > 12.
Alltså b = 4 när P = 12 och då c = 5.
En annan sorts lösning
Pytagoras sats ger c² = a² + b², alltså c² – b² = a² = 9, vilket enligt konjugatregeln ger (c + b) * (c – b) = 9, men c + b = P – a = 12 – 3 = 9, alltså 9 * (c – b) = 9, alltså c – b = 1. Ledvis summering av c + b = 9 och c –b = 1 ger 2 * c = 10 och c = 5.
Vi verifierar att en rätvinklig triangel med kateter 3 och 4 verkligen har hypotenusan 5, däremot frågar vi nu inte om det finns flera lösningar, vårt resonemang visade ju att hypotenusan måste vara 5.
För andra värden på parametrar P och a, ger denna metod rimliga svar om a > 0 och P > 2 * a. Man får då c = (a² / (P – a) + P – a) / 2 och b = P – a – c. (Stämmer formeln på P = 12 och a = 3?)
Ha en trevlig sommar!
Innehåll: LR
