Den här månaden har det kommit lösningar från David Ström, gymnasielärare i matematik/fysik, Ystad (komvux); Vera P. i Lilla Adolf Fredrik skola, Stockholm; Sofie, Cecilia, Michaela och Simon i 8a på Svensgårdsskolan i Ödåkra (lärare: Sara Karlton); Ebba A.; Samuel W. i Ystad samt Ida och Oskar i 5F Fryxellska skolan, Västerås.
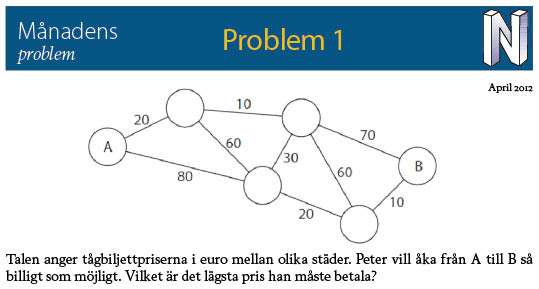
Svar: 90 euro
Någon åkte lite vilse men till slut hittade alla den billigaste vägen. Ett knep kan vara att radera de sträckor som man vet att Peter inte ska åka eftersom det finns billigare omvägar. Det finns billigare omvägar till de sträckor som kostar 60, 70 eller 80 euro och när man har raderat dem så finns bara en väg kvar.
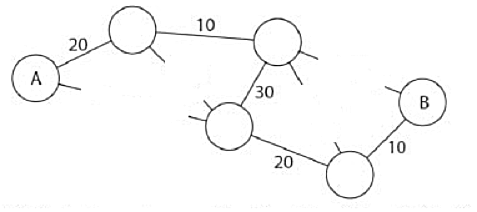
Denna metod fungerar för just den kartan, men skulle man ha en annan karta, en t ex med 40 städer och 100 järnvägsträckor mellan dem, så skulle det säkert finnas kvar ett otal möjliga vägar från A till B även efter radering av de onödigt dyra sträckorna.
Här visas en metod som skulle vara lämplig om man ville hitta den billigaste resan från A till B och hade ett stort antal vägar att välja mellan.
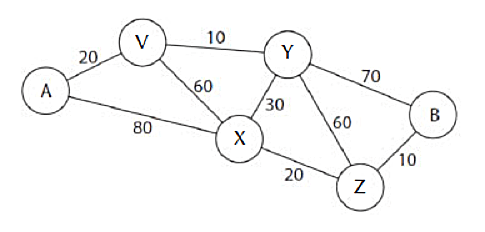
För att beräkna den lägsta kostnaden för en resa från A till en stad med högst n byten, tar man kostnader av resor med högst n-1 byten till dess ”grannstäder”, (städer med en direkt järnvägsförbindelse), lägger till priset för den sista sträckan och sedan väljer det billigaste av alternativen.
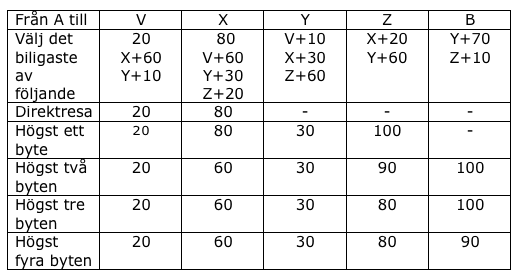
Resan till någon av dessa städer blir inte billigare med ännu fler byten.
En skicklig programmerare kan säkert ”snabba upp metoden” d v s ändra den så att man med färre beräkningar ändå kommer fram till samma resultat.

Svar: Talet är 262
Ida och Oskar svarar 182 (218-182=36). Också ett intressant resultat, bara det, att ni hade förväxlat vilket tal skulle vara störst och vilket minst. Den vanligaste metoden är att behandla problemet som ett sifferpussel. Vera beskriver det så här:
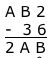
B måste vara 6 eftersom att 2-6 inte går, jag lånar 1 från B och då blir det 12.
12-6=6
Nu har jag lånat 1 från 6.
6-1=5
5-3=2
A är då 2.
AB2=262
Kontroll:
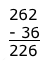
David skriver både om ”pusselmetoden” och om olika lösningar med hjälp av ekvationer:
”Jag ställde upp ekvationen (100a-10b-c) – (100c+10a+b) = 36 <=> 90a+9b-99c = 36 <=> 10a+b=11c+4, som har lösningar för alla värden på c. Sedan läste jag uppgiften lite noggrannare och såg att c=2. Alltså blir talet 262, eftersom 262-226=36, något som man enklare kunnat komma fram till genom att ställa upp differensen
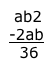
som ger b=6 och a=2.”
Det är lite besvärligt att lösa en ekvation med två eller tre obekanta. (Den har oändligt många heltalslösningar men vi är bara intresserade av de i mängden {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.) Låt oss tänka det tresiffriga talet med tvåan på slutet som en sammansättning av ett tvåsiffrigt tal T följt av siffran 2. När tvåan flytas får man 2 följt av T som ska vara 36 mindre. Sambandet kan uttryckas med följande ekvation:
10*T+2 – 36 = 200+T (ekvation med bara en obekant: T),
den förenklas till 9*T = 234 och ger lösningen T=26.
Alltså det sökta talet är 262 (och 226 efter flyttning av tvåan).
Ersätter man tvåan med en annan siffra C, så får man T=11*C+4 som ger ett ensiffrigt T, (T=4) för C=0, tvåsiffriga T för C mellan 1 och 8 och ett tresiffrigt (T=103) för C=9.
Ebba skriver bara så här:
”Uträkning: 222-222=0
Differens 36: 262-226=36
Svar: 262”
Kanske tänkte Ebba så här (här skrivet med Veras beteckningar): ”Med A=2 och B=2 blir differensen 0. Ökar man B med 1, så ökar differensen med 9. För att få differensen 36 måste man öka B med 4, alltså B=2+4=6.”
Oklart om Ebba tänkte så. I lösningar av problem tre återkommer vi till metoden att undersöka förändringar för att från tillståndet i ett läge kunna förutse tillstånden i andra lägen.
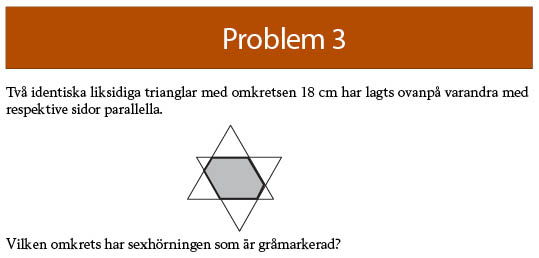
Svar: 12 cm
En lösning gjord av Sofie, Cecilia, Michaela och Simon:

Ni har räknat sidan B två gånger och hoppat över G. De är faktiskt lika långa eftersom de små trianglarna är lika stora i varje par av småtrianglar som ligger mittemot varandra i figuren. Det kan man bevisa t ex med hjälp av symmetrin eller genom att jämföra de stora trianglarnas höjder, de små trianglarnas höjder och avståndet mellan (de parallella) baserna. Men ni skulle egentligen inte behöva använda det om ni valde en annan, (en horisontell) sida som D.
David inleder med att undersöka några specialfall och gränsfall, i alla visar sig sexhörningen ha omkrets 12cm och sedan konstaterar han att på grund av de små trianglarnas, ”uddarnas”, liksidighet blir halva 6-hörningens omkrets alltid lika med en sida på triangeln: 18/3 = 6 cm. David använder alltså symmetrin fullt ut, sexhörningen består av två identiska halvor, så det räcker med att bestämma längden på bara en av dem.
Här kommer en bildlig lösning:
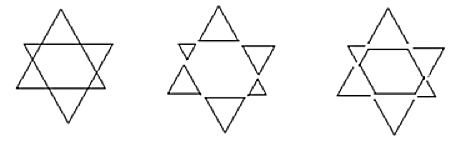
Två trianglar med omkretsar 18cm var, har den sammanlagda linjelängden 18cm+18cm= 36cm. De sex små trianglarna består av samma linjer, alltså 36cm sammanlagt. En av 3 lika långa sidor i varje liten triangel tillhör sexhörningen, 36cm/3= 12cm.
Här kan vi också se att även om trianglarna skulle vara olika stora men fortfarande liksidiga och parallella så skulle sexhörningens omkrets vara lika med summan av de 2 trianglarnas sidolängder.
Vera påstår att: ”Oavsett hur vi flyttar trianglarna blir det samma resultat, bara om de flyttas parallellt.” Detta är sant. Varje parallellförflyttning kan göras i två steg ett parallellt till ett par triangelsidor och ett parallellt till ett annat och det räcker att bevisa att i varje flyttsteg förblir omkretsen oförändrat. Här kommer ett bildbevis:
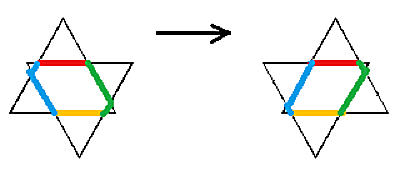
Vi delar sexhörningen i fyra delar och färglägger dem med fyra färger. Vid en parallellförflyttning av den övre triangeln horisontellt till höger bevarar varje del sin längd, den blåa och den gröna ändrar bara formen. Hela sexhörningen bevarar sin omkrets. Sedan målar vi om sexhörningen och gör en likadan förflyttning snett neråt:
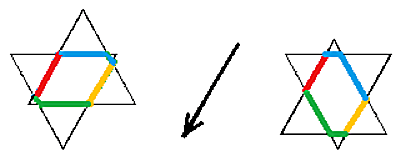
och sexhörningen bevarar sin omkrets igen.
Detta är ett lite annorlunda sätt att tänka: Man beräknar sexhörningens omkrets i ett speciellt läge, t ex det mest symmetriska, då är var och en av sexhörningens sidor 2cm och omkretsen 12cm och då vet man att den måste vara 12cm i samtliga lägen.
Metoden är kraftfullare än de föregående. Nu kan man bevisa att även om två liksidiga trianglar inte är parallella med varandra, så bevaras sexhörningens omkrets i alla fall. Den gången i varje steg förflyttar man en triangel parallellt med en bisektris till två motstående sidor i sexhörningen. (Gäller också olika stora liksidiga trianglar.)
Ett par trianglar som inte är liksidiga kan ändå ha samma egenskap: Omkretsen av den gemensamma sexhörningen förblir oförändrad trots att en av trianglarna parallellförflyttas. Annars finns det i alla fall en flyttriktning som bevarar sexhörningens omkrets.
Innehåll: LR
