Det har kommit lösningar från:
Simon på Tundalsskolan i Robertsfors;
Henning F L från Schola Europaea, Luxembourg;
elever på Torpaskolan i Vänersborg (med läraren Gunilla Fridh);
Klasserna 2 och 3 på Karlshögsskolan i Malmö (läraren Sinikka Lindgren);
Elin från Sanduddens skola i Stockholm;
Vera P. i Lilla Adolf Fredrik skola 3a, Stockholm;
Ida och Oskar i 5F i Fryxellskaskolan i Västerås;
en elev i Rönnskolans särskola L/M i Piteå (med läraren Helen Pohjanen);
David Ström, gymnasielärare ma/fy, Forum Ystad;
26 elever i åk 5 i Errarps skola, Ängelholm (med läraren Anna Arvidsson);
elever vid Stenhammarskolan i Lidköping;
arbetslaget Stenen åk 3-5 på elevernas val ”Matteverkstad”(lärare Per Anders Malm)
samt från Max och Lisa Ö.
De flesta svarade på alla 3 problemen.
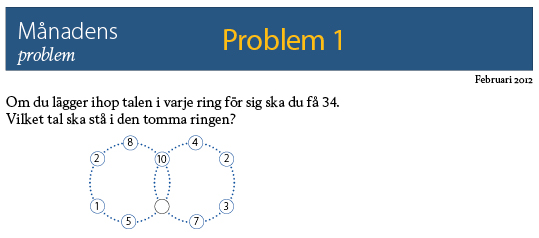
Svar: 8
Man väljer en av de stora ringarna, t ex den vänstra, lägger ihop de tal som syns i ringen, 5+1+2+8+10= 26. Då saknas det 8 till 34. Därför ska i den tomma ringen stå 8. Man kan på samma sätt göra med den högra ringen, 10+4+2+3+7= 26, 34-26= 8. De flesta som har svarat räknade på två sätt, både i den vänstra ringen och i den högra ringen och det är bra att göra så. Får man samma resultat i båda fallen, så vet man att man har räknat rätt, annars räknar man på nytt tills man får det att stämma.
Men vad ska man göra när man har räknat noggrant och kollat igen och man ändå får ett resultat i den vänstra ringen varje gång och ett annat i den högra? Ja, då måste det vara ett fel på problemet och man skickar ett meddelande till Månadens problem att något inte stämmer. Genom ett tekniskt missöde föll de två nedersta små ringarna i figuren bort, när vi lade februariproblemen ut på nätet. Efter ett meddelande från Vera P. fick vi skyndsamt åtgärda detta.
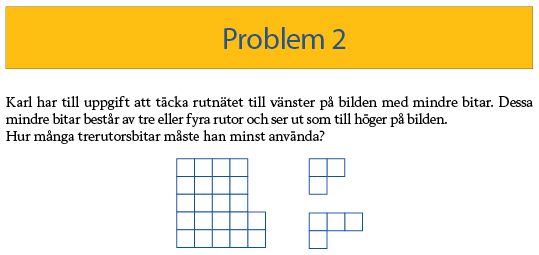
Svar: 2
Man måste använda minst 2 trerutorsbitar (plus 4 fyrarutorsbitar) för att täcka rutnätet utan att bitarna överlappar varandra eller sticker ut. Och det kan man göra på många sätt. Bland över 30 svar var nästan alla olika. Här kommer några exempel:

Elever i Stenhammarskolan i Lidköping sa att det var lite som spelet ”Ubongo”.
När man söker en lösning behöver man kanske rita på prov flera gånger då är det enklast och snabbast att rita av rutnätets kontur på rutat papper och markera bitarna så här:
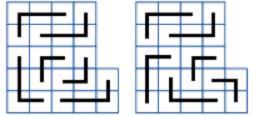
Självklart kunde Karl vrida bitarna innan han lade dem på plats, annars skulle det inte gå. Så varje bit kunde se ut på flera olika sätt:

men en sådan figur,
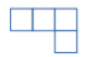
en spegelbild av fyrarutorsbiten, kunde han inte få bara genom att vrida fyrrutersbiten liggande platt. Han måste lyfta den och vända eller just spegla den i en spegel. De flesta lösningar har sådana spegelvända fyrrutorsbitar men inte alla.
Några elever trodde att Kalle måste använda minst 6 trerutorsbitar, därför att det var den bästa lösningen de kom på, som t ex den här:

Duktigt men inte en av de allra bästa. Av en märklig anledning kom inte några lösningar med 3 eller 4 trerutorsbitar, jag undrar varför. Och förresten, kan vi vara säkra på att 2 verkligen är det bästa möjliga svaret bara därför att det var det bästa vi lyckades hitta?
Vera och David beräknade att rutmönstret består av 22 rutor och att med 2 trerutorsbitar täcker man 6 rutor och restande 16 rutor täcker man med 4 fyrarutorsbitar: 2*3+4*4=22. Kanske i dessa siffror kan vi finna svar på våra frågor?
Hur skulle det gå med bara en trerutorsbit? Den skulle täcka 3 rutor såklart. Men hur många fyrarutorsbitar behöver vi nu för att täcka de 19 rutor som blir kvar? … utan att de överlappar varandra eller sticker ut? Det går inte därför att 19 inte är delbart med 4.
22 kan skrivas som summa av ett naturligt tal delbart med 3 och ett delbart med 4 bara på två sätt:
22= 6+ 16 eller 22= 18+4 dvs. 2*3+4*4 eller 6*3+1*4. Därför kan inte en 22-rutors figur täckas på annat sätt än med 2 trerutorsbitar och 4 fyrarutors eller 6 trerutors och en fyrarutors.

Svar: Johanna står mellan Sara och Fredrik.
Följande bild kom från elever på Torpaskolan i Vänersborg:
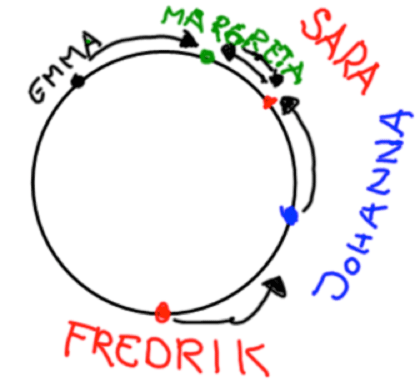
Här ser vi vem som står bredvid vem och vem som nämner vem (pekar med pilen) och att han eller hon verkligen nämner den som står närmast.
Det kom ovanligt många rätta svar på problem 3, många av dem med bilder men det var få som lyckades att placera barnen på sådana avstånd från varandra att påståendet ” Var och en säger namnet på sin närmaste granne.” stämde. Eller kanske slarvar man med detta. Man tror att om man ställer barnen i rätt ordning och låter varje barn nämna en av sina grannar så att varje namn sägs det givna antal gånger, så man kan justera avstånden efteråt så att även de stämmer. Det går att göra i detta fall men inte alltid.
Låt 5 barn stå olika långt från varandra. Om varje barn säger namnet av det barn som står närmast, är det då möjligt att varje namn sägs en gång? ”Klart att det är möjligt” – svarar nog många – ”om varje barn säger namnet på det som står näst till höger i en ring, så var och en nämns en gång”. Men försök anpassa avstånden så att de stämmer. Det går inte. Det går inte och inte på något annat sätt heller. Rätt svar på frågan är: Nej, det är omöjligt.
Max och Lisa tar upp avstånden i sin beskrivande lösning: Johanna står mellan Fredrik och Sara. Vi ritade, och då står Margareta och Sara närmast, så de säger varandra, på andra sidan Margareta står Emma, Emma säger Margareta. På andra sidan Sara står Johanna, och Johanna säger Sara. På andra sidan Johanna står Fredrik, men längre bort, och Fredrik säger Johanna. Då hamnar Fredrik längre från Emma än Johanna.
I Veras lösning stämmer avstånden. Resonemangslösningen som följer saknar ett par viktiga steg och förklaringar, men roligt att någon försöker:
Veras svar: Johanna står mellan Sara och Fredrik.

”Eftersom jag vet att Emma står bredvid Margareta som nämns 2 gånger, så vet jag att Sara måste stå bredvid Margareta för att hon också nämns 2 gånger. Eftersom Johanna nämns 1 gång måste hon stå mellan Fredrik och Sara. Fredrik nämner Johanna, Johanna nämner Sara, Sara nämner Margareta, Margareta nämner Sara och Emma nämner Margareta.”
Låt mig förklara det bättre. Två av fem barn som står i en ring, står antingen bredvid varandra eller har ett tredje barn mellan sig. De två som står bredvid Sara nämner Sara, de två som står bredvid Margareta nämner Margareta. Ingen nämner både Sara och Margareta, alltså ingen står mellan Sara och Margareta, alltså Sara och Margareta står bredvid varandra. På samma sätt vet vi att ingen står mellan Fredrik och Emma eftersom varje barn nämner en av sina grannar men varken Fredrik eller Emma nämns, alltså Fredrik och Emma står bredvid varandra. Vi har nu tre par som tillsammans bildar en kedja: Fredrik-Emma-Margareta-Sara. Johanna har kedjans ändpunkter till sina grannar, alltså hon står mellan Fredrik och Sara.
Innehåll: LR
