Svar och lösningar, jan 2011

I hålet passar två pusselbitar. Vilka?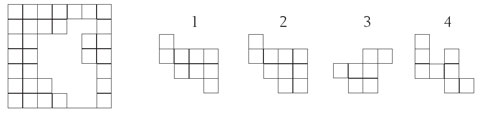

Lösning
2 och 3.
En lösning vi fått är av Dennis Gudmundsson, åk 3 Kiaby skola.
“Först provade jag alla fyra. Då såg jag att 3:an passade där uppe och tvåan passade där nere.” En enkel och bra lösning.

Man kan diskutera vad som egentligen menas med att en pusselbit passar i hålet och vad menas med att 2 pusselbitar passar i hålet. En rimlig tolkning av det andra är att man kan lägga de två över hålet så att de täcker hela hålet utan att överlappa varandra och utan att någon sticker utanför hålet. När man söker EN som passar i hålet så är man intresserad av en som kan läggas över hålet så att den har en och bara en del av omkretsen gemensam med hålet och utan att den sticker ut.

Om man råkar ut för ett liknande men svårare problem, så det är bra att veta att det finns metoder att förenkla provandet. Vi beräknar areor: hålet är 17 rutor, pusselbitarna är 9, 10, 7 och 8. Summan av pusselbitarnas areor måste vara lika med hålets area om de ska passa in. Endast bitarna 1 och 4 eller bitarna 2 och 3 kan möjligtvis passa (9+8=17 och 10+7=17). En ännu mer avancerad metod är att beräkna omkrets: Hålet har omkretsen 22 enheter, pusselbitarna 1 och 4 har 16 och 18. Vi drar slutsatsen att om bitarna 1 och 4 tillsammans ska passa i hålet, så måste de gränsa med varandra med 6 kantsidor. Lägger vi dem bredvid varandra och vrider på alla möjliga sätt så ser vi att det är omöjligt. Nu återstår bara bitarna 2 och 3. Sist försöker vi fylla hålet med bitarna 2 och 3 för att förvissa oss att de verkligen passar.

Mittpunkten i kvadraten KLMN är punkten O. Vinklarna AOB och COD är båda räta. Kvadratens sidlängd är 2 cm. Vilken area har den skuggade delen?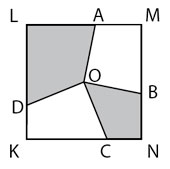
A) 1 cm² B) 2 cm² C) 2,5 cm² D) 2,25 cm² E) det beror på hur man väljer punkterna B och C

Lösning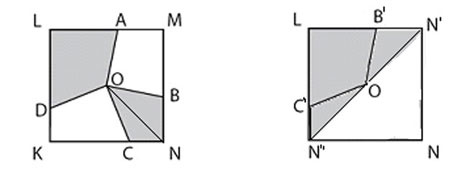
2 cm².
Dela ett av de skuggade fyrhörningarna, tex OBNC, i två trianglar OBN och ONC genom att dra en diagonal från O till kvadratens hörn N.

Rotera triangeln OBN runt punkten O 90grader moturs och triangeln ONC 90grader medurs. De skuggade områdena bildar nu tillsammans en likbent rätvinklig triangel LN’N’’ med kateter 2cm. Den har area 2cm*2cm/2=2 cm².

En annan lösning: Betrakta en av de vita fyrhörningarna tex OCKD. Vi tar bort övriga 3 områden och förlänger linjerna CO och DO.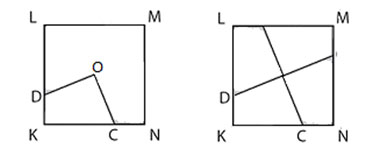

Nu är kvadraten uppdelad i 4 kongruenta fyrhörningar. (Hela figuren är rotationssymmetrisk.) Dessa fyrhörningar har lika stora areor 2cm*2cm/4=1 cm². Alltså OCKD har arean 1 cm². På samma sätt ser vi att OAMB har arean 1 cm², alltså det skuggade området har arean
4 cm² – 1 cm² – 1 cm² = 2 cm².

I en låda ligger tre röda kort, tre gröna kort, tre gula kort och tre blå kort. De tre korten av respektive färg är numrerade 1, 2 och 3. Tre kort tas på måfå ur lådan. Vilket av följande händelse är mest sannolik?
A) De tre korten är av samma färg
B) De tre korten har alla olika nummer
C) De tre korten är alla av olika färg
D) De tre korten har samma nummer
E) Alla uppräknade händelser är lika sannolika

Lösning
C. De tre korten är alla av olika färg.
Lösning 1: Vi beräknar sannolikheten för händelse A: ”De tre korten är av samma färg”.
Vi tar första kortet på måfå ur lådan. Det spelar ingen roll vilket det blev. Det finns 11 kort kvar i lådan, därav två av samma färg som det först dragna kortet. Sannolikheten att det andra kortet blir av samma färg är 2/11. Vi drar nästa kort. Om det andra kortet blir av samma färg som det första så finns det 10 kort kvar i lådan, därav en av samma färg som de två först dragna korten. Sannolikheten att det tredje kortet blir av samma färg är 1/10. Sannolikheten att både det andra och det tredje kortet blir av samma färg som det första är (2/11)*(1/10)=1/55.
Med samma metod beräknar vi att sannolikheten för händelse B är (8/11)*(4/10)=16/55.
För händelse C: (9/11)*(6/10)=27/55.
För händelse D: (3/11)*(2/11)=3/55.
Det mest sannolika är alltså händelse C, den har sannolikhet 27/55.

Lösning 2: Vi beräknar hur många utfall som ingår i händelse A, dvs hur många 3-kortkombinationer finns så att alla tre kort är av samma färg. De är fyra. Alla tre röda kort, eller alla tre gröna kort, eller alla tre gula kort, eller alla tre blå kort.
För händelse B finns 4*4*4=64 kombinationer därför att för varje nummer vi kan välja färg på fyra sätt.
För händelse C finns 4*3*3*3=108 kombinationer (vi kan välja färg som inte ska vara med på fyra sätt och för varje färg som ska vara med kan vi välja nummer på tre sätt.
För händelse D finns det 3*4 kombinationer. (Eftersom två olika kort med samma nummer har olika färger så måste de tre kort som alla har samma nummer vara av olika färger. Vi kan på tre sätt välja nummer som ska vara gemensam för dessa tre kort och på fyra sätt den färg som inte ska vara med.) Händelse C består av flest kombinationer: 108, och alla kombinationer är lika sannolika. Alltså C är mest sannolik.