Svar och lösningar, nov 2010

Denna månad har vi fått lösningar från Michaela Stjerndal, 8B i Sundbyskolan, Spånga, Tintin Lindström i 4A på Minervaskolan i Umeå samt Daniel Khodarahmi.

Alla barn i Adams och Evas klass har ställt upp sig på ett led efter varandra. Bakom Adam står 16 barn. Ett av dem är Eva. Framför Eva står 14 barn. Ett av dem är Adam. Mellan Adam och Eva står det 7 barn. Hur många barn står uppställda i ledet?

Lösning
23 barn.
En lösning som faktiskt kan göras i klassrummet mer alla elever:
16 barn står bakom Adam och ett okänt antal framför honom. Det kan presenteras så här:

ooooooooooooooooA ?

Ett av barnen bakom Adam är Eva och mellan Adam och Eva står 7 barn, så Eva är det åttonde barnet bakom Adam.

ooooooooEoooooooA?

Nu ser man att det står 8 barn plus ett okänt antal (?) framför Eva och de skulle vara 14. Det okända antalet är alltså 14-8=6.

ooooooooEoooooooAoooooo

Vi räknar: 8 barn + Eva + 7 barn + Adam + 6 barn = 8+1+7+1+6 = 23 barn.

En algebraisk lösning:
Framför Eva står Adam. Det är 7 barn som står mellan Adam och Eva. Det står ett okänt antal barn, x, framför Adam. Det ska sammanlagt ge 14 barn. Det ger ekvationen 1+7+x=14 med lösningen x=6. Alltså 6 barn står framför Adam. Adam, de 16 som står bakom honom och 6 framför honom ger 1+16+6=23 barn i ledet.

En kombinatorisk lösning:
Om vi räknar barn som står bakom Adam och barn som står framför Eva får vi 16+14= 30 och då har vi räknat alla barn i ledet eftersom varje barn står antingen bakom Adam eller framför Eva eller både och. Sen räknar vi bort de barn som vi räknat två gånger, dvs de som står mellan Adam och Eva. 30-7= 23.

Summan av fem på varandra följande heltal är 2005. Vilket är det största av de fem talen?

Lösning
403.
En lösning med hjälp av statistik:
Det mittersta av de 5 talen är också dess medelvärde. När summan är 2005 så är medelvärdet 2005/5 = 401. Det största av de 5 talen är 2 större än det mittersta, alltså 403.

En lösning med algebra:
Kalla det första av talen x. De påföljande 4 talen är: x+1, x+2, x+3 och x+4. Ekvationen x+x+1+x+2+x+3+x+4=2005 ger x=399. Det största av de 5 talen är x+4= 399+4= 403.

Bilden föreställer tre halvcirklar. Ändpunkterna A och B på den övre halvcirkeln ligger rakt ovanför mittpunkterna E och F till de två undre halvcirklarna. Om varje halvcirkel har radien 2 cm, hur många cm² är arean av det skuggade området?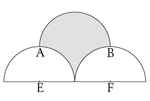

Lösning
8 cm².
De lösningar som skickas in har använt formeln för cirkelns aren. Här behöver man dock inte använda denna.
En lösning:
Vi delar det gråa området i fyra delar med hjälp av två räta linjer, en vågrät genom A och B och en lodrät genom mittpunkten av den övre halvcirkeln och tangeringspunkten mellan de två undre halvcirklarna. Vi får fyra figurer av vilka vi kan bygga två kvadrater, varje med sidan 2. Sammanlagda arean är alltså 2×2cm×2cm= 8cm².

Några varianter av den första lösningen:
Man kan på flera sätt dela området i tre delar och bygga en 2×4 rektangel av dem. (En liten modifiering av den första lösningen.) Eller, kanske det allra klyftigaste, dela den i tre delar så att man av dessa kan bygga en kvadrat med sidolängden 8. (Två av de tre ska vara cirkelsegment.)