Svar och lösningar, sep 2010

Denna månad har vi fått lösningar från klass 2d på Stora Högaskolan, Fredrik Holm år 7 på Lunds skola i Forsa samt Timmie Namuth som är 13 år.

I varje ruta på brädet ska en av siffrorna 1, 2 eller 3 skrivas in. Varje rad och varje kolumn ska innehålla alla tre siffrorna. Harry har börjat fylla i rutorna.
Vad kan han skriva i rutan med frågetecknet?

Lösning
3.
Detta är sudoku i miniatyr. En viktig princip för den som löser sudoku är: Ska alla 3 siffror (9 i en vanlig sudoku) stå i en rad eller kolumn med tre (9) rutor så får det inte vara fler än en av varje, för då skulle inte alla få plats.

En lösning: I andra raden saknas bara en trea. Den får Harry skriva in i rutan till höger. Han får inte skriva några fler treor i högra kolumnen så i övre hörnet till höger får det stå något annat än en trea. Alltså måste första radens trea stå i rutan med frågetecknet.

En annan lösning: Det kan inte stå en etta i rutan med frågetecknet. Harry får testa med en tvåa eller trea. Han skriver en tvåa med blyertspenna. Då blir det en trea i övre högra hörnet. När han ser att ingenting passar i andra raden till höger, raderar han de två siffror som han skrivit och börjar om med en trea i frågeteckenrutan, tvåa i hörnet. Nu går det bra, trea i andra raden till höger och i tredje raden ska det stå 3,2,1.

Bilden innehåller sex lika stora cirklar som precis får plats i en rektangel. En mindre rektangel har sina hörn i fyra av cirklarnas mittpunkter. Denna mindre rektangel har omkretsen 60 cm. Vilken omkrets har den större rektangeln?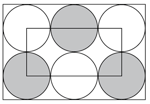

Lösning
100 cm.
Lika stora cirklar har lika stora radier. Den mindre rektangelns kortsida består av 2 radier och dess långsida av 2 radier och en diameter vilket är samma som 4 radier. Dess omkrets är 2*(2+4)=12 radier. Alltså en radie är 60 cm/12=5 cm och en diameter 10 cm.
Den större rektangeln har längd 3 diametrar och bredd 2 diametrar och därmed omkrets 2(3+2)=10 diametrar dvs. 100 cm.

Vilket av följande tal kan skrivas som produkten av fyra olika heltal som alla är större än 1?
A: 625 B: 124 C: 108 D: 2187 E: 2025

Lösning
2025.
Varje naturligt tal kan ses som ett paket av primtal. Vi har 4 sådana paket:
625 = 5 * 5 * 5 * 5 är ett paket med 4 femmor
124 = 2 * 2 * 31
108 = 2 * 2 * 3 * 3 * 3
2187 = 3 * 3 * 3 * 3 * 3 * 3 * 3
2025 = 3 * 3 * 3 * 3 * 5 * 5
(En etta är ett tomt paket och en nolla är en bottenlös brunn eller ett svart hål.)
Nu gäller det att packa om ett av dessa fem paket till fyra olika små paket som inte är tomma. Om vi gör fyra paket av 625 så blir alla fyra likadana. 123 duger inte heller, det innehåller bara tre primtal.

108 innehåller fem primtal. Vi får göra ett paket med två primtal och tre paket med bara ett primtal var. Men då behövs tre olika primtal och vi har bara två. Så det går inte.

2187 innehåller enbart treor. Ska paketen vara olika så måste de i så fall vara olika stora: den minsta med minst en trea, nästminsta med minst två, en med åtminstone tre och en med fyra eller fler treor. Då behöver vi minst 10 treor och vi har bara 7. Det går inte.

2025 innehåller fyra treor och två femmor. Vi slår ihop två treor till 9 och en trea med en femma till 15 och en trea och en femma återstår. Det gick! 2025=9*15*3*5.

Man kan undra om vi verkligen har undersökt alla möjligeter för de fyra första talen. Kan inte något av talen faktoruppdelas på ett annat sätt och ses som ett annat paket? Aritmetikens fundamentalsats säger att detta är omöjligt.