Svar och lösningar, jan 2010

Undersök när summan av tre positiva heltal är delbara med 3 om:

a) alla tre talen är lika stora
b) precis två av talen är lika stora
c) talen är konsekutiva, dvs är i ordningsföljd

Lösning
a) Summan av tre lika stora tal är delbar med tre.
Algebraiskt kan detta uttryckas: a + a + a = 3a. Vi kan konstatera att högerledet innehåller en faktor 3, och är alltså delbart med 3.

b) Här är det lite svårare att finna mönster, men har vi hittat ett exempel så kan vi få ett till genom att öka på respektive tal med 1, se exemplen nedan.
Och nu lite algebra. När det gäller delbarhet med 3 så finns tre intressanta typer av tal: 3n, (3n+1) och 3n+2), där bara det första är delbart med 3. Detta skrivsätt täcker alla positiva heltal för n-värden större eller lika med noll. Vi delar upp problemet i dessa tre typfall:

1) 3n + 3n = 6n Vi ser att om nästa tal är av typ 3m så är summan delbar med 3, eftersom 6n + 3m = 3(2n + m). Exempel: 3+3+9 = 15 om n=1 och m=3

2) (3n + 1) + (3n + 1) = 6n +2. Vi ser att om det andra talet är av typ 3m+1 så är summan delbar med 3, eftersom 6n +2 + 3m +1 = 3( 2n +m + 1). Exempel: 4+4+10=18 om n=1 och m=3

3) (3n+2) + (3n+2) = 6n +4. Vi ser att om det andra talet är av typ 3m + 2 så är summan delbar med 3, eftersom: 6n +4 + 3m +2 = 3(2n + m +2). Exempel: 5+5+11=21 om n=1 och m=3

Ett mönster är alltså att talen skall vara av samma ”typ” om summan ska vara delbar med 3.

c) Vi kan först testa med några fall och finner då att alla summor är delbara med 3. Kan det rent av finnas något släktskap med a-uppgiften? Det tredje talet är ju 1 större än det mittersta och det första talet är 1 mindre. Därför kan vi skriva summan som tre mittental. Kallar vi det mittersta talet a, så får vi:
(a – 1) + a + (a + 1) = a + a + a = 3a

c-uppgiften visar sig vara en variant av a-uppgiften!

Medelvärdet av tio olika positiva heltal är lika med 10. Hur stort kan det största av talen vara som mest?

Lösning
I det här fallet är det bra att ”tänka baklänges”. Vi har ett resultat och vi vill hitta en lösning som har med problemets förutsättningar att göra. Eftersom resultatet ska vara 10 så måste summan av de tio talen vara lika med 100. Ett av talen ska vara så stort som möjligt, vilket leder till att de andra bör vara så små som möjligt, men ändå olika. Summan av dessa blir då
1+2+3+4+5+6+7+8+9 = 45. Det tionde och största talet är alltså 100 – 45 = 55.

Placera en punkt inuti en liksidig triangel så att summan av avstånden från punkten till triangelns sidor blir så liten som möjligt. Motivera lösningen.

Lösning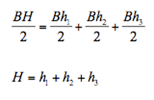
Vi kan börja med att placera en punkt lite snett någonstans inne i triangeln. Avstånden från punkten till sidorna markerar vi med sträckor vinkelrätt mot respektive sida.
Som så ofta när det gäller geometriska problem gäller det nu att dra lämpliga ”hjälplinjer”. Det brukar vara bra att dra hjälplinjer mellan punkter, så vi kan testa att förbinda vår utsatta punkt med triangelns hörn. Då ser vi att den liksidiga triangeln nu blir indelad i tre trianglar som har respektive ”avstånd” som höjd.
Vi vet också att summan av de tre deltrianglarnas area är lika med hela triangelns area. Men eftersom alla dessa trianglar har lika stor bas B (den liksidiga triangelns sida) så följer att summan av de tre höjderna är lika med hela triangelns höjd H. Algebraiskt kan detta skrivas:

Den något överraskande slutsatsen är alltså att punkten kan placeras var som helst, summan av avstånden är alltid lika med hela triangelns höjd. Detta gäller även ”extrema” fall, t.ex. om man placerar punkten i ett av triangelns hörn.