Svar och lösningar, april 2009

Lösningar till månadens problem har skickats in av Sture Sjöstedt.

Greta promenerar längs stigen från vänster till höger. När stigen delar sig måste hon välja den ena stigen. Hon vänder inte och går tillbaka. Längs stigen hittar hon lappar med bokstäver på. Dem plockar hon upp och lägger i sin korg. Vilka bokstäver kan hon få i korgen?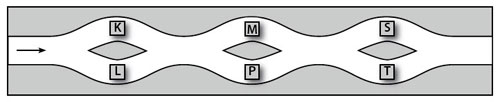

Lösning
L, M och S är en av uppsättningar med lappar. Det finns fler.
En lapp med K eller L, en med M eller P samt en med S eller T.

Fyra pojkar köpte en present till sin far. Ett av barnen gömde presenten. Modern frågade dem vem som hade gömt presenten. De fyra pojkarna kom med följande påståenden:
Alfred: ”Det var inte jag! ”
Benjamin: ”Det var inte jag! ”
Christian: ”Det var Daniel! ”
Daniel: ”Det var Benjamin! ”
Precis en av pojkarna lurades. Vem hade gömt presenten?

Lösning
Daniel luras.
Om Alfred luras så luras även Christian och Daniel. Om Benjamin luras så luras även Christian
och Daniel. Om Christian luras så luras även Benjamin. Om Daniel luras så talar de övriga sanning.

Om man vet att log(√2005 +√1995 )=n,
vilket värde har då log(√2005 – √1995 )?

A: n – 1 B: 1 – n C: 1n D: n + 1 E: Omöjligt att avgöra

Lösning
B.
log (√2005 +√1995 ) =n.
log ((√2005 +√1995 )(√2005 – √1995 )) =log(2005 – 1995) = log10 = 1.
log((√2005 +√1995 )(√2005 – √1995 )) =log(√2005 +√1995 ) + log(√2005 – √1995 ).
Det ger:
log(√2005 +√1995 ) + log(√2005 – √1995 ) = n + log(√2005 – √1995 ) = 1.
log(√2005 – √1995 ) = 1 – n.