Svar och lösningar, mars 2009

Lösningar till månadens problem harskickats in av klass 6a på Hovshagaskolan i Växjö samt Mikael Lindqvist och Linda Karlsson i klass 9a på Storåsskolan, Lindesberg

Robert bygger en tunnel av små likadana klotsar. När han tröttnar på tunneln bygger han en pyramid istället. Hur många av klotsarna från tunneln blir över när han har byggt sin pyramid?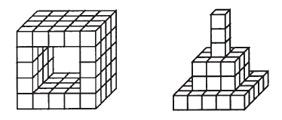

Lösning
18 st.
Till tunnelbygget behöver Robert: 4 · 5 klotsar = 20 klotsar till bottenplattan och lika många till taket, sammanlagt 40 klotsar. De två sidoytorna innehåller vardera 3 · 4 klotsar, dvs sammanlagt 24 klotsar. Totala antalet klotsar som krävs för tunnelbygget är 40 + 24 = 64. I pyramiden innehåller bottenlagret 5 · 5 = 25 klotsar. De två följande lagren innehåller vardera 3 · 3 = 9 klotsar, totalt 18 klotsar och överst är det 3 klotsar. Antalet klotsar för pyramidbygget är 25 + 18 + 3 = 46.
Antalet klotsar som blir över är 64 – 46 = 18.

De tre skålarna P, Q och R är ordnade från vänster till höger efter stigande vikt. Var ska den fjärde skålen placeras för att viktordningen ska behållas?

Lösning
Mellan P och Q.
Från skålarna P och Q drar vi slutsatsen att ”triangeln” väger mindre än ”cirkeln”.

En låda äpplen kostar 2 euro, en låda päron kostar 3 euro och en låda plommon kostar 4 euro. Åtta lådor frukt kostade 23 euro. Vilket är då det största möjliga antalet lådor med plommon?

Lösning
3 st.
När man prövar med 5 och 4 lådor plommon, så går det inte att få ihop åtta lådor frukt för 23 euro. Med 3 lådor plommon, 1 låda päron och 4 lådor äpplen går det.