Svar och lösningar, september 2007

Problem 1

Det ligger fem kort på bordet. De ligger så här:



Det gäller att få korten ordnade 1, 2, 3, 4, 5. Varje gång måste man låta två kort byta plats med varandra.
Hur många omgångar behövs?

Lösning: Ett förslag är att byta kort 2 och 5, sedan 1 och 2 samt 3 och 4.

Vi har också fått en lösning från Alice och Alva i Halmstad:
Hej vi har kommit på ett sätt, vi flyttar runt lapparna 3 gånger.
4:an byter plats med 3:an,
2:byter plats med 1:an,
och 5:an byter plats med 1:an.
Det här var en av lösningarna vi kom på några fler.
Alice och Alva

Problem 2

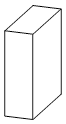
Du har ett stort antal byggblock som alla har längden 1 dm, bredden 2 dm och höjden 3 dm.



Hur många sådana block går det minst åt för att bygga en kub?

Lösning: Volymen på ett byggblock är 6. Kubens volym är något tal upphöjt i 3, men måste också vara delbart med 6. Sidorna, 1, 2, 3, 4 och 5 dm är alltså inte möjliga. En kub med sidan 6 går dock att bygga genom att bygga en kvadratisk bottenplatta med höjden 1 dm av 6 byggblock och sedan lägga sex sådana kvadrater ovanpå varandra. För att få en kub behövs det sex sådana plattor, dvs 6 x 6 = 36 tegelstenar.

Problem 3

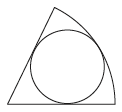
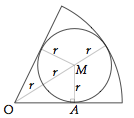
På bilden är förhållandet mellan cirkelsektorns radie och den inskrivna cirkelns radie 3:1.



Då är förhållandet mellan deras areor

A) 3:2 B) 4:3 C) 5:3 D) 6:5 E) 5:4

Lösning:



Anta att den inskrivna cirkeln har radien r och arean πr². Då har cirkelsektorn radien R=3r. Dra radien R i cirkelsektorn genom den inskrivna cirkelns medelpunkt M. Den rätvinkliga triangeln OAM är en halv liksidig triangel. Det ger att cirkelsektorns medelpunktsvinkel är 60°, och dess area är π(3r)²/6=3πr²/2. Förhållandet mellan areorna är 3:2.
problemen …
Array 		lösningarna …
Array

Innehåll: UD