Om Diamantdiagnoserna
Om Diamantdiagnoserna
Inledning och beskrivning
Diamant är ett diagnosmaterial i matematik som består av 127 diagnoser, avsedda för grundskolan. Tanken med diagnoserna är att de ska användas av dig som lärare för att kartlägga hur långt eleverna kommit i sin matematikutveckling. Syftet är i huvudsak formativt och diagnoserna ska ge ett underlag för planering av en strukturerad undervisning som skapar goda förutsättningar för eleverna att nå kunskapskraven. Därigenom blir det möjligt att förebygga framtida svårigheter i matematik som de annars kan hamna i beroende på bristande förkunskaper eller färdigheter.
En avgörande faktor för att kunna planera en väl strukturerad undervisning för den enskilda eleven, och för att bedriva en individualiserad undervisning, är god kännedom om var eleven befinner sig i sin matematiska utveckling. Tanken är därför att du ska använda diagnoserna kontinuerligt för att följa elevens kunskapsutveckling under flera år. Tydliga mål för undervisningen och en kontinuerlig uppföljning är avgörande faktorer för elevens framgång.
Diagnosernas användning
Avsikten med diagnoserna i Diamant är att de ska användas som en naturlig del av undervisningen. I allmänhet ges en diagnos till alla, eller de flesta av eleverna. Ibland kan en diagnos innehålla några uppgifter som vissa av eleverna ännu inte mött. I så fall kan dessa elever få hoppa över de uppgifterna. Vid andra tillfällen kanske du vill ge diagnoser enbart till en mindre grupp av elever och kanske väljer du då ut vissa speciella uppgifter. Man kan sammanfatta diagnosernas användning så här:
• Du kan ta reda på om alla elever har nödvändiga förkunskaper inför ett nytt moment i undervisningen.
• Du kan använda diagnosmaterialet för att identifiera elever som behöver större utmaningar för att undvika att dessa elever känner sig understimulerade i matematikundervisningen. Även elever som kommit långt i sin kunskapsutveckling bör kartläggas.
• Du kan med hjälp av en diagnos stämma av din undervisning genom att efter ett genomgånget avsnitt ta reda på om undervisningen lett till uppställda mål.
• Du kan ta reda på om en uppföljning eller ett åtgärdsprogram lett till önskat resultat.
Du som lärare avgör själv utifrån kännedom om dina elever vem som ska göra vilken diagnos och när.
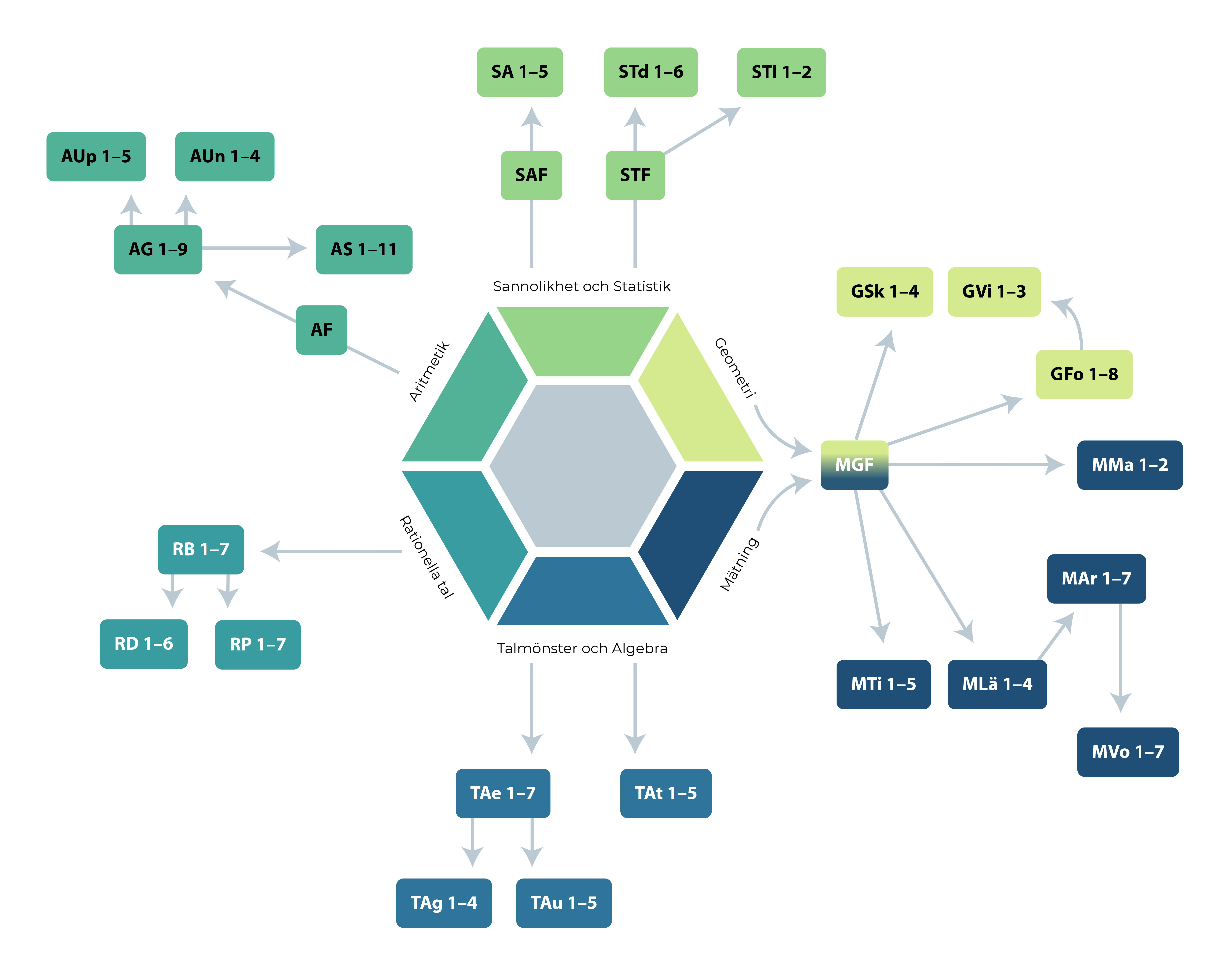
Varje område är i sin tur indelat i delområden. Som exempel finns inom området Mätning följande delområden:
- Mätning av tid
- Mätning av massa
- Mätning av längd
- Mätning av area
- Mätning av volym
Inom varje delområde finns ett antal diagnoser av varierande svårighetsgrad, vilka testar olika aspekter av för området centrala begrepp.
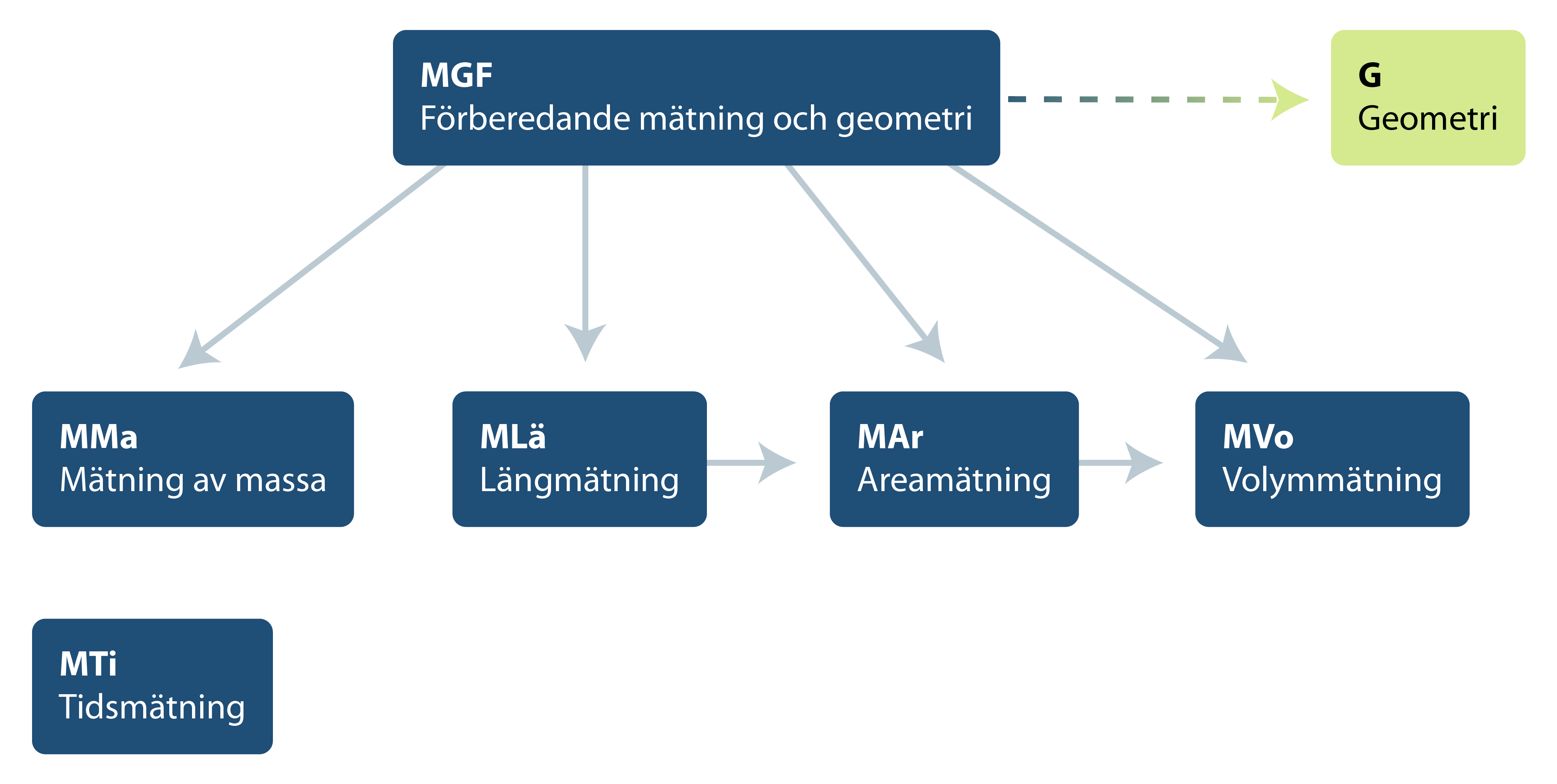
Matematiken är uppbyggd på ett logiskt sätt och har en egen struktur. Varje moment kräver därför sina speciella förkunskaper. Med hjälp av strukturscheman (schematiska skisser som visar relationen mellan olika delområden/diagnoser) kan du se om, och i så fall hur, varje delområde/diagnos är kopplat till ett eller flera andra delområden/diagnoser.
Av strukturschemat ovan, som gäller för Mätning, framgår att Mätning av längd bör föregå Mätning av area men att Mätning av längd och Mätning av tid inte är beroende av varandra. Det kan även finnas kopplingar mellan olika områden. Viss aritmetik kan till exempel vara förkunskap till uppgifter som finns inom mätning. Ett exempel på detta är att förståelse av decimaltal är en förkunskap till enhetsbyten. Som framgår av det här strukturschemat är diagnos MGF, Förberedande mätning och geometri, även förkunskap till området Geometri.
Tack vare strukturschemat finner du diagnoser som kanske täcker ett innehåll som du inte brukar ta upp den årskurs som du undervisar. Dessa diagnoser kan emellertid vara lämpliga att använda för elever som kommit långt i sin kunskapsutveckling. På samma sätt finner du diagnoser som eleven borde klarat under tidigare årskurser men som kan vara lämpliga att använda i senare årskurser för de elever som ännu inte nått relevanta kunskapskrav. Vi vill emellertid poängtera att alla elever bör ges möjlighet att få sina kunskaper i matematik kartlagda, var och en på sin kunskapsnivå och att detta även gäller elever som kommit långt i sin matematikutveckling.
Till varje område/delområde hör ett avsnitt kallat Didaktiska kommentarer där det ges en beskrivning av det didaktiska ämnesinnehåll som diagnoserna bygger på. Dessa kommentarer är relativt komprimerade eftersom en översiktlig beskrivning av viktiga didaktiska aspekter av områdets innehåll ska beskrivas och täcka in utveckling och progression av innehållet från förskoleklass till årskurs 9. Om du undervisar i de tidigaste årskurserna behöver du inte i detalj vara insatt i hela matematikinnehållet upp till årskurs 9. Olika delar av kommentarerna blir intressanta för olika lärare beroende på i vilka skolår man undervisar. Men ett viktigt syfte med kommentarerna är att visa på hur all matematikinlärning hänger ihop och på vilket sätt redan den tidiga matematikförståelsen blir en viktig utgångspunkt för det fortsatta lärandet. I det avseendet är kommentarerna av vikt för alla lärare.
Till varje diagnos finns även en Beskrivning av de ingående uppgifterna, om diagnosens Genomförande, tankar om vad en Uppföljning kan innehålla och ett Facit.
Under rubriken Genomförande beskrivs om det är något speciellt du bör tänka på då diagnosen genomförs. Där anges till exempel om det behövs något hjälpmedel såsom linjal eller gradskiva och hur lång tid det brukar ta att genomföra diagnosen. Vidare finns en Resultatblankett till varje diagnos. Resultatblanketten har till syfte att ge dig en snabb överblick över diagnosresultatet på såväl individsom gruppnivå. Dessutom finns ett Utvecklingsschema där du på individnivå kan sammanställa en elevs diagnosresultat och dina observationer om elevens utveckling i matematik.
Med hjälp av resultatblanketten som du kan fylla i efter varje diagnos ser du om det är något moment som en stor del av gruppen ännu inte behärskar eller om det enbart gäller enstaka elever. Diagnosresultaten ger dig således underlag för att planera din undervisning såväl för den enskilda eleven som för hela gruppen. Till varje diagnos hör också ett avsnitt rubricerat Uppföljning. Där ges en kort beskrivning av vad som kan vara orsak till vissa typer av fel och förslag på hur du genom undervisning kan komma till rätta med de vanligaste problemen.
Utgående från en skriftlig diagnos kan du avgöra om en elev har vissa svårigheter men inte alltid orsakerna till dem. Enstaka elevers diagnosresultat bör därför följas upp med intervjuer eller kompletterande övningar där eleven ges tillfälle att närmare redovisa sina räknestrategier eller tankar.
Muntliga fördiagnoser
Till områdena Aritmetik, Mätning och Geometri samt Sannolikhet och Statistik finns muntliga fördiagnoser. Med hjälp av dessa kan du exempelvis vid skolstart (när du ska starta med det aktuella området) se hur långt olika elever kommit i sin matematikutveckling. Den muntliga fördiagnosen i grundläggande aritmetik har visat sig lämplig att genomföra i slutet av förskoleklassen.
Kontinuitet och generalisering
Vid formativ bedömning i matematik är kontinuitet och generalisering centrala begrepp. Kursplaner består ju inte av ett antal isolerade moment utan de olika momenten är sammanflätade i ett förkunskapsmönster. Som exempel är goda färdigheter i grundläggande subtraktion inte ett mål i sig. Den här färdigheten ska i själva verket återanvändas i en rad andra situationer, t.ex. vid huvudräkning och skriftlig räkning. Den är också en integrerad del i en god taluppfattning. Såväl förståelsen av olika subtraktionsstrategier som färdigheten att använda dem måste därför ha en sådan kvalitet att den kan generaliseras till nya områden och därmed ge kontinuitet i inlärningen.
I en god taluppfattning ingår ett antal grundläggande strategier för huvudräkning såsom att 72 − 39 kan beräknas genom lika tillägg av 1. Detta ger den betydligt enklare subtraktionen 73 − 40. På motsvarande sätt kan 28 · 25, med användning av den associativa räknelagen beräknas som 7 · 4 · 25 och divisionen 35/7 uppfattas både som delningsdivision och som innehållsdivision. I det första fallet delas 35 upp i 7 delar och i det andra fallet undersöks hur många gånger 7 ryms i 35.
Strategier av det här slaget ska inte bara fungera för naturliga tal. När eleven kommer till decimaltalen ska de vara så säkra på den här typen av strategier att de med kontinuitet kan generaliseras till rationella tal. När eleven t.ex. ska beräkna 7,2 − 3,9 ska eleven direkt kunna använda någon av följande strategier. Antingen genom att utföra beräkningen i enheten tiondel, vilket ger 72 − 39 = 73 − 40 = 33 tiondelar, alltså 3,3 eller att göra ett lika tillägg av 0,1 vilket ger 7,2 − 3,9 = 7,3 − 4,0 = 3,3. Vid en multiplikation som 0,7 · 50 kan man använda sig av den associativa räknelagen, vilket ger 0,7 · (10 · 5) = ( 0.7 · 10) · 5 = 7 · 5 = 35. Divisioner som 3,5 / 0,7 behöver heller inte vålla några problem. Här kan man antingen räkna i enheten tiondel vilket ger divisionen 35 / 7 eller använda sig av innehållsdivision vilket leder till frågan hur många gånger
0,7 ryms i 3,5.
Vid planering av undervisningen är det angeläget att du som undervisar i tidigare årskurser är medveten om hur det innehåll du arbetar med kommer att generaliseras under senare årskurser. På motsvarande sätt är det angeläget att du som undervisar i senare årskurser är medvetna om vilka kunskaper eleverna har med sig från tidigare och på vilket sätt man med kontinuitet kan generalisera dessa kunskaper. Det är detta som är den bärande idén i en strukturerad planering. För att underlätta arbetet med en strukturerad planering finns det i Diamant strukturscheman på olika nivåer. Genom att följa pilarna i dessa strukturscheman får man ett underlag, dels för en strukturerad planering, dels om vilka kunskaper som krävs inför ett nytt innehåll.
Aktiv och passiv kunskap
För att till en viss del se kvalitet i elevens kunskaper har vi vid uppgiftskonstruktionen valt att skilja mellan aktiv och passiv kunskap. Detta kan säkert vara till hjälp vid bedömning av elevens kunskaper inom ett moment i området. Ett exempel på detta är diagnosen RB1. På den första uppgiften är andelarna redan skuggade och eleverna behöver bara avläsa andelen, en typ av passiv kunskap.
1
Hur stor del av figuren är skuggad?
a) __________
b) __________
c) __________
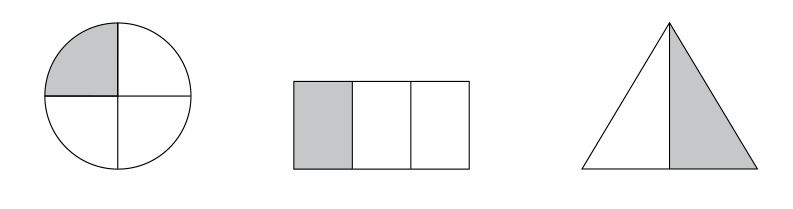
På den tredje uppgiften finns det ett rutnät i figurerna och eleverna får själva skugga andelen. Här visar eleven ett mer aktivt kunnande.
3
a) Skugga en sjättedel av figuren
b) Skugga en fjärdedel av figuren
c) Skugga en tredjedel av figuren

- Conceptual understanding – förståelse av begrepp, operationer och samband.
- Procedural fluency – förmåga att utföra beräkningar med variation, effektivt och korrekt.
- Strategic competence – förmåga att formulera, representera och lösa matematiska problem.
- Adaptive reasoning – förmåga till logiskt tänkande och reflektioner samt att kunna förklara och motivera.
- Productive disposition – att se matematik som viktig, användbar och värd att studera kopplat till tron på sin egen förmåga.
- Täckningsgraden beskriver de olika aspekter som kompetensen täcker. När det t.ex. gäller argumentationskompetens, så har kompetensen hos den som kan föra en argumentation högre täckningsgrad än hos den som bara kan följa argumentationen.
- Aktionsradien beskriver de olika situationer och områden av matematiken som kompetensen omfattar. Det kan handla om att lösa problem algebraiskt, geometriskt eller grafiskt.
- Den tekniska nivån beskriver hur tekniskt avancerade situationer kompetensen omfattar, alltså vilka matematiska modeller en person förmår använda vid problemlösning.
Vad diagnoserna inte innehåller
De ovan beskrivna förmågorna i kursplanens syftestext låter sig inte prövas i enskilda diagnoser och omfattas därför inte av diamantdiagnoserna. Eftersom intresse och tilltro till sin förmåga hänger intimt samma med hur en elev lyckas utveckla sina kunskaper inom kursplanens centrala innehåll, kommer diamantdiagnoserna ändå att spela en stor roll även när det gäller elevers intresse och förmåga. Med hjälp av diagnoserna testas om eleverna har det begreppsförråd och det verktygsförråd som krävs för att utveckla sitt matematikkunnande vidare. Det ger en trygghet och ökad motivation för eleven att veta vad hon kan och vad hon behöver träna mera på liksom för läraren att veta vad undervisningen bör innehålla framöver.
Att diagnostisera problemlösning och kommunikativ förmåga låter sig inte göras med denna typ av diagnosinstrument. En orsak till detta är att såväl problemlösning som kommunikation förutsätter en given kontext (sammanhang). För att en sådan kontext ska bli realistisk måste den anpassas till varje klass, grupp och elev. En annan orsak är att en viktig aspekt av problemlösning är att kunna resonera, argumentera och välja olika lösningsstrategier. Det är således inte problemets lösning i sig som är intressant utan förmågan att se olika lösningar och att kunna generalisera dem till nya obekanta situationer. Som en konsekvens av detta, kartläggs elevers kunskaper i problemlösning bäst i en annan form såsom till exempel i muntliga situationer. Detsamma gäller för huvudräkning. Även detta innehåll bör behandlas i dialog med eleverna där just reflektionen över valda strategier blir viktig liksom att diskutera strategierna och värdera dess för och nackdelar i olika situationer. För att kunna vara effektiv problemlösare, argumentera och diskutera samt använda effektiva huvudräkningsstrategier krävs dock redskap i form av automatiserad talfakta, begreppsförståelse och terminologi. Syftet med diagnoserna i Diamant är att säkerställa att eleverna har tillgång till dessa verktyg som i sin tur är en förutsättning för att kunna genomföra en problemlösning eller huvudräkning. Vissa uppgifter som till exempel i diagnos AG4, där generaliserade tabellkunskaper testas, är givetvis en typ av huvudräkningsuppgifter och uppgifter på diagnoser inom geometrin som GFo7, har karaktären av problemlösning eftersom det är ett sätt att testa om eleven kan använda relevanta begrepp.
En vanlig fråga om Diamant gäller i vilken årskurs eleverna ska behärska de olika diagnoserna. Eftersom olika skolor och klasser har stor frihet att lägga upp sin undervisning och planering på sitt eget sätt, kan man inte ange i vilken årskurs, en viss diagnos skall göras. Detta betor helt på din planering och i vilken ordning du valt att arbeta med olika innehåll. Däremot kan du med hjälp av diagnosmaterialet Diamant skaffa dig en god uppfattning om elevernas aktuella kunskaper i avsikt att på sikt öka elevens kunskapsutveckling i ämnet matematik.
Vetenskapliga reflektioner och överväganden
Syftet med den här texten är att beskriva hur innehållet i diagnosmaterialet Diamant förhåller sig till aktuell forskning och kunskapssyn. Här beskrivs även den teorigrund på vilken materialet vilar, hur det är uppbyggt och hur det kan användas.
Synen på skolämnet matematik
För att ge en bakgrund till diagnosernas uppbyggnad ger vi här vår syn på skolämnet matematik och vad det innebär att lära matematik. Abstraktion är en väsentlig del av kunskapsutvecklingen i matematik. Det innebär att eleverna ska lära sig att använda ett antal grundläggande matematiska modeller mentalt, alltså utan stöd av konkretirserande material. Dessa modeller ska senare på ett flexibelt sätt kunna användas för att kommunicera, generalisera och lära mera matematik, för att tolka omvärlden och för att studera andra skolämnen. Med hjälp av diagnoserna ska man kunna se vilka kunskaper som eleven behärskar och i vilken utsträckning eleverna lyckats abstrahera det ämnesinnehåll som beskrivs i kursplanen i matematik.
Enligt Nationalencyklopedin är matematik en ”…abstrakt och generell vetenskap för problemlösning och metodutveckling /…/ den har frigjort sig från det konkreta ursprunget hos problemen vilket är en förutsättning för att den ska vara generell, dvs. tillämpbar i en mångfald situationer”. Även skolans matematik syftar till abstraktion vilket är en förutsättning för att komma vidare i kunskapsutvecklingen. Sven-Erik Liedman (2001) påpekar att ”Redan påståendet att två plus två är lika med fyra utgör en svindlande abstraktion i förhållande till den konkreta verkligheten: två äpplen eller två tankar gör ingen skillnad” (s. 102).
I skolan går ofta vägen till abstraktion via konkretisering. För att göra skolans matematik generell och funktionell måste eleven emellertid lämna konkretiseringen bakom sig och abstrahera. Konkretiseringen får således inte bli ett mål utan det krävs att eleven lär sig abstrahera redan i de tidigare årskurserna. Detta har varit en utgångspunkt vid konstruktionen av diagnosmaterialet Diamant.
För att lösa ett matematiskt problem räcker det inte med att förstå problemet och att ha en lösningsmetod. Det krävs dessutom så goda räknefärdigheter att eleven också kan utföra de beräkningar som krävs för att få ett korrekt svar. Behärskar inte eleven sådana färdigheter blir lösningen oftast felaktig, eller kräver så mycket tankekraft, att eleven får svårigheter med att bearbeta den primära uppgiften. Man kan uttrycka detta som att eleven då saknar flyt i sitt räknande på samma sätt som en del elever kan sakna flyt i sitt läsande. Det är angeläget att diagnoserna inte enbart kartlägger begreppsförståelse, utan också att eleverna har så goda färdigheter att de får flyt i sitt räknande och sin kommunikation. Detta har under senare år allt mer betonats i internationell didaktisk forskning (Loewenberg Ball, FerriniMundy, Kilpatrick, Milgram, Schmid & Schaar, 2005).
Skolmatematiken i internationell forskning
Efter internationella jämförelser ansåg sig USA behöva öka elevernas kunskaper i matematik. Man tillsatte av det skälet en grupp bestående av framstående matematikdidaktiker och matematiker för att utarbeta en gemensam grundsyn på skolans matematikinnehåll, Common ground (Loewenberg Ball m.fl., 2005). Centrala punkter som man kom överens om var:
- Automatical recall of basic facts. Man menade att vissa procedurer och algoritmer inom matematiken är så grundläggande och är så generellt tillämpbara att de måste behärskas med automatik.
- Calculators. Miniräknare bör användas även i de lägre årskurserna, men, påpekar man, de måste användas med stor försiktighet så att man inte äventyrar inlärningen av basala kunskaper.
- Learning algorithms. Eleverna ska med säkerhet kunna använda algoritmerna för de fyra räknesätten. Samtidigt är det viktigt att de förstår hur algoritmerna är uppbyggda och fungerar. Ett skäl för detta är att algoritmerna bygger på strukturen i vårt talsystem med basen 10 och därmed förstärker elevernas taluppfattning.
- Fractions. Förståelsenavbråkärviktigeftersomdet är omöjligt att på djupet förstå förhållande, proportionalitet och procent utan att behärska bråk. Bråk är också en nödvändig förkunskap för algebran.
- Teacher knowledge. En effektiv undervisning förutsätter att läraren förstår den matematik som det undervisade innehållet bygger på. Det räcker alltså inte med att behärska det just aktuella innehållet utan läraren måste dessutom kunna se detta innehåll i ett större perspektiv och förstå de underliggande matematiska idéerna.
Man kan konstatera att forskare i USA har tagit klar ställning i dessa frågor och vi som arbetat med diagnosmaterialet Diamant delar i stort den syn på skolans matematikinnehåll som redovisas i Common Ground (Loewenberg Ball m.fl., 2005).
Individens uppfattning om matematiska begrepp
Skolans matematikundervisning syftar till att eleven ska behärska ett antal centrala matematiska begrepp. Det är dessa begrepp som sedan, på ett flexibelt sätt, ska kunna användas i en rad olika situationer. Dessa begrepp är emellertid inte statiska utan de utvecklas och förfinas efter hand. Ett nödvändigt villkor är därför att de begrepp som erbjuds eleverna i undervisningen ska vara utvecklingsbara för att främja ett fortsatt lärande. Ett diagnosinstrument måste därför bygga på teorier för hur skolans matematikinnehåll kan struktureras på ett logiskt sätt och vilka förkunskaper som krävs för att utveckla olika begrepp till en högre begreppsnivå (Ma, 1999; Löwing, 2002). Det är detta som beskrivs till vänster i nedanstående figur, där ringarna representerar de nya förkunskaper (F) som krävs för att utveckla begreppet A vidare från en nivå till nästa. Även om begrepp kan byggas upp på olika sätt, kan man inte gå hur som helst mellan olika begrepp och begreppsnivåer. Matematiken har en inneboende struktur som är hierarkisk men inte linjär.
Vad figuren ovan visar är inte bara kopplingen mellan olika begreppsnivåer och i vilken utsträckning eleven har uppfattat begreppen. Däremellan ligger undervisningsprocessen som omfattar planering, presentation av innehåll, arbetsformer, arbetssätt m.m. Även om detta är viktiga inslag i undervisningen, så kan allt detta inte kartläggas med hjälp av ett nationellt diagnosmaterial. Vad Diamant fokuserar på är elevernas uppfattningar av olika begrepp. Mindre bra resultat på en diagnos kan emellertid ofta härledas till brister i undervisningsprocessen. När det gäller teorier för ämnesinnehållet, alltså det vi kallar didaktisk ämnesteori, så har denna beskrivits i Marton (1986), Schulman (1986, 1987), Kilborn (1989, 2005a,b), Ball och Bass (2000) samt i Löwing (2002, 2004, 2008, 2011). En viktig del av denna teori omfattar analyser av vilka förkunskaper som krävs och vilka strategier som kan användas inom olika områden av skolmatematiken. Denna teori har tidigare använts för att bygga upp andra diagnosinstrument (Johansson & Kilborn, 1982). Detta överensstämmer väl med det omfattande ramverk för formativ bedömning som Wiliam och Thompson (2007) beskriver och som omfattar tre centrala processer: nämligen att fastställa var eleven befinner sig i sin kunskapsutveckling, vilka målen är och vilket innehåll eleven behöver förstå för att nå målen.Eleverna lyckas i vår studie inte med att hålla isär de olika resonemangskedjorna. Eleverna reder inte ut hur logiken ser ut och vilka argument som är giltiga i ett givet ögonblick. Istället anförs skäl, belägg eller information hörande till olika matematiska modeller utan att man frågar sig om just den aktuella modellen kan ta hänsyn till detta. (s. 227)
Krav på en funktionell diagnos
Redan i samband med PUMP-projektet (Kilborn, 1979) gjordes ett grundläggande arbete som omfattar såväl en teori för diagnosers innehåll som en teori för urvalet av uppgifter och synen på validitet och reliabilitet. Det är detta arbete vi utgått från och vidareutvecklat i diagnosmaterialet Diamant. En förutsättning för att ett diagnosinstrument ska fungera är att det har god validitet som anger i vilken utsträckning ett mätinstrument mäter vad det avser att mäta och reliabilitet som mäter förekomsten av tolkningsfel. När det gäller validiteten så är tre faktorer viktiga:- Diagnosinstrumentet ska hjälpa läraren att få reda på kvalitet och omfattning av de begrepp och metoder som eleven har tillägnat sig utifrån en didaktisk förkunskapsstruktur.
- Uppgifternaiendiagnosbörbaradiagnostiseraett avgränsat innehåll i sänder. Om uppgifterna blir komplexa och berör flera olika innehåll samtidigt är risken stor att man inte kan avgöra vari elevens eventuella kunskapsluckor består. Detta påverkar i sin tur diagnosens reliabilitet.
- Uppgifternas konstruktion och antal måste vara sådant att man med stor säkerhet kan kartlägga elevens svårigheter. I annat fall får man inte utrett, och därmed inte möjligheter att åtgärda dessa, vilket kan komma att utgöra hinder vid elevens fortsatta matematikinlärning.
Diagnosernas uppbyggnad
Diagnoserna bygger på väl kända och allmänt accepterade forskningsresultat om hur barn tillägnar sig matematik. Det är t.ex. känt att det inom områden såsom Aritmetik, Mätning/geometri och Statistik krävs en förförståelse för att komma vidare. Till dessa områden finns därför muntliga diagnoser för att kartlägga elevernas förförståelse av grundläggande begrepp och termer. Diagnoserna i Grundläggande aritmetik skiljer sig från övriga diagnoser. Det beror på att subtraktioner som 7 – 5 och 14 – 8 eller multiplikationer som 7 · 8 bör vara så väl automatiserade att eleverna med flyt, alltså utan att extra tankekraft, ska kunna använda dessa som delberäkningar vid såväl skriftlig räkning och huvudräkning som vid problemlösning. Sådana uppgifter förekommer därför i homogena grupper omfattande sex uppgifter. Målet är att eleverna ska behärska dessa uppgifter på ett sådant sätt att alla uppgifterna blir rätt inom ett begränsat tidsintervall. Uppgifterna på de övriga diagnoserna är av en annan karaktär och bygger i stället på en sekvensering där komplexitetsnivån successivt höjs och olika aspekter av begreppet prövas. Det betyder att man som lärare kan avgöra vilken nivå och vilka aspekter respektive elev behärskar och vad som fattas för att eleven ska komma vidare. Inom det här området finns det en mångårig erfarenhet vid Göteborgs universitet, Institutionen för didaktik och pedagogisk profession, vilket framgår av referenslistan. De gjorda erfarenheterna bygger i sin tur på en omfattande internationell forskning som bedrivits av bl.a. Gelman & Galistel (1983), Schulman (1986, 1987), Carpenter & Moser (1984), Fennema, E., Carpenter, Franke, Jacobs & Empson, (1996), Ma (1999), Ball (2000), Ball & Bass (2000) och Clarke (2001) samt Kilpatrick m.fl. ( 2001). Materialet är uppbyggt på liknande sätt som Wiliam (2007) lyfter fram så att det kan användas som ett verktyg för olika ändamål:- för att kartlägga och följa upp den enskilde elevens kunskapsutveckling.
- för att kartlägga och följa upp gruppens eller klassens kunskapsutveckling
- för att analysera måluppfyllelsen i skolan eller kommunen och synliggöra eventuella behov av kompetensutveckling.
Litteratur och källor
Ball, D. (2000). Working on the Inside: Using One’s Own Practice as a Site for Studying Teaching and Learning. In A. Kelly & R. Lesh (Eds.), Research Design in Mathematics and Sciene Education (pp. 365–402). Mahwah, NJ: Laurence Erlbaum.
Ball, D., & Bass, H. (2000). Interweaving Content and Pedagogy in Teaching and Learning to Teach: Knowing and Using Mathematics. In J. Boaler (Ed.), Multiple Perspectives on Mathematics Teaching (pp.83–104). Westport: Ablex Publishing.
Carpenter, T., & Moser, J. (1984). The aquisition of addition and subtraction concepts in grades one through three. Journal for Research in Mathematics Education, 15(3), 179–202.
Clark, D. (2001). Complementary Accounts Methodology. In D. Clark (Ed.), Perspectives on Practice and Meaning in Mathematics and Science Classrooms (pp. 13–32). Dordrecht: Kluwer Academic Publishers.
Fennema, E., Carpenter, T. P., Franke, M. L., Jacobs, V. R., & Empson, S. B. (1996). A Longitudinal Study of Lerning to Use Children ́s Thinking in Mathematics Instruction. Journal for research in Mathematics Education, 27:403–434.
Gelman, R., & Galistel, C. R. (1983). The child’s understanding of number. In M. Donaldson, R. Grieve, & C. Pratt (Eds.), Early childhood development and education. Oxford: Basil Blackwell.
Johansson, B., & Kilborn, W. (1982). Räkning. Stockholm: Utbildningsförlaget.
Häggström, J. (2008). Teaching systems of linear equations i Sweden and China. (Göteborg Studies in Educational Sciences 262) Göteborg: Acta Universitatis Gothoburgensis.
Kilborn, W. (1979a). PUMP-projektet. Bakgrund och erfarenheter. (Utbildningsforskning, FoU rapport 37). Stockholm: Skolöverstyrelsen.
*Kilborn, W. (1979b). Ämnesmetodiska processanalyser i matematik inom KomVux. Stockholm: Högskolan för lärarutbildning.
Kilborn, W. (1989). Didaktisk ämnesteori i matematik. Del 1: Grundläggande aritmetik. Stockholm: Utbildningsförlaget.
*Kilborn, W. (1996), On national assessment. A study about goals and results in grade 5. Maputo, Mocambique: National Institute for Educational Development (INDE).
Kilborn, W. (2005a). Manual de didactica de matamática. Volum 1 e volum 2. Cardernos de Pesquisa n016. Maputo: Instituto Nacional do Desenvolvimento da Educação (INDE ).
Kilborn, W. (2005b). O primeiro ano com um novo curriculo. Maputo: Instituto Nacional do Desenvolvimento da Educação (INDE ).
*Kilborn,W., Dhliwayo, N., Gudza, E.& Ngaru, M., (1996). A Study of State of Mathematics Education in the Zimbabwean Primary Schools. Göteborg: Göteborgs Universitet, Institutionen för ämnesdidaktik. Harare Zimbabwe: CDU Ministry of Education.
Kilpatrick, J., Swafford, J., & Findell, B. (Eds.). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press.
Liedman, S-E. (2001). Ett oändligt äventyr. Om människans kunskaper. Stockholm: Bonnier.
Loewenberg Ball, D., FerrineMundy, J., Kilpatrick, J., Milgram, R.J., Schmid, W. & Schaar, R. (2005) Reaching for Common Ground in K-12 Mathematics Education.
Löwing, M. (2002). Ämnesdidaktisk teori för Matematikundervisning. Ämneskunskapens relation till individ och omvärld. (IPD-rapport nr 2002:11) Göteborg: Göteborgs Universitet, Institutionen för pedagogik och didaktik.
Löwing, M. (2004). Matematikundervisningens konkreta gestaltning. En studie av kommunikationen lärare–elev och matematikens didaktiska ramar. (Göteborg Studies in Educational Sciences 208) Göteborg: Acta Universitatis Gothoburgensis.
Löwing, M. (2008). Grundläggande Aritmetik – Matematikdidaktik för lärare. Studentlitteratur: Lund.
Löwing, M. (2011). Grundläggande geometri – Matematikdidaktik för lärare. Studentlitteratur: Lund.
*Löwing, M. & Kilborn, W. (2000). Mathematics in Foundation Phase. Department of Education in the Nothern Cape Province and SIDA (Swedish International Development Authority). Kimberley, Sydafrika
*Löwing, M., & Kilborn W. (2002) Baskunskaper i Matematik, för skola, hem och samhälle. Studentlitteratur. Lund
*Löwing, M., & Kilborn, W. (2003) Huvudräkning. En inkörsport till matematiken. Studentlitteratur Lund.
Löwing, M., & Kilborn, W. (2008) Språk, kultur och matematikundervisning. Studentlitteratur Lund.
Ma, L. (1999). Knowing and teaching elementary mathematics. Mahwah NJ: Lawrence Erlbaum.
Marton, F. (Red.). (1986). Fackdidaktik volym III. (s. 87–101). Lund: Studentlitteratur.
Nationalencyklopedin (1989–1996). Höganäs: Bra Böcker.
*Nilsson, G. (2005). Att äga π. Praxisnära studier av lärarstudenters arbete med geometrilektioner. (Göteborg Studies In Educational Sciences 228) Göteborg: Acta Universitatis Gothoburgensis.
Niss, M., & Højgaard Jensen, T. (2002). Kompetencer og matematiklæring. Ideer og inspiration til udvikling af matematikundervisning i Danmark. Köpenhamn: Uddannelseministeriet.
Riesbeck, E. (2008). På tal om matematik. Linköping: Institutionen för beteendevetenskap och lärande.
Schulman, L. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4–14.
Schulman, L. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57 (1), 1–22.
Wiliam, D. (2007). Keeping learning on track. In F. Lester, (Ed.) Second Handbook of Research on Mathematics Teaching and Learning. Charlotte, NC: NCTM
Wiliam, D., & Thompson, M. (2007). Integrating Assessment with Instruction: What Will It Take to Make It Work. In C.A. Dwyer, (Ed.) The Future of Assessment: Shaping Teaching and Learning. Mahwah N.J.: Lawrence Erlbaum Associates.
* Betecknar litteratur som inte är direkt nämnd i denna sammanställning, men som har sitt ursprung i, och belyser den forskning inom matematikdidaktik och diagnostisering, som bedrivits vid Göteborgs universitet och som utgör en viktig kunskapsbas för detta diagnosmaterial.