- Lösningar har kommit från:
Olof L och Kiana R på Futuraskolan
Matilda H i 5A samt Hilda B och Sandra B i 5C på Kastellgårdsskolan, Kungälv (lärare: Joanna Aho)
Wilhelm S och Wiggo A i 4–6 Korn och 4–6 Råg, Vedums skola
klass 1A och 1B på Långsättersskolan, Nyköping (lärare: Josefin Thorsten)
Linn och Engla, åk 6, Idenorsskola, Hudiksvall
Klass 3–4 Lila på Grossbolskolan, Forshaga (lärare: Mari Lindström)
Vera P i 6E, Vasa Real, Stockholm
Lösning på problem 1
Svar: Julie måste ta bort 2 mynt.
Det får bara finnas två mynt i varje rad och i varje kolumn och det finns bara fyra rader och fyra kolumner i diagrammet, så det ska finnas 8 mynt i diagrammet. Två mynt måste bort. Och det går, nedan visas två sätt att göra det på.
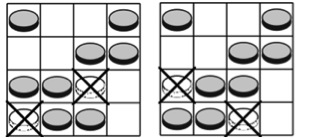
Även elever i klass 1 klarade problemet.
Så beskriver Josefin Thorsten en lektion:
”Detta löste vi genom att testa – kolla om det stämmer – testa igen. Eleverna arbetade i par och diskuterade sig fram till vilka cirklar som skulle bort, och ibland vilka som de inte kunde ta bort. När de löst problemet fick de testa att lösa det igen fast man inte fick ta bort samma mynt. Hade de löst det första gången var det betydligt enklare att lösa det igen.”
Lösning på problem 2
Svar: 4 av 8, 6 av 15 och 3 av 20.
8 stenar i högen:
Andreas tar 4 stenar för att hindra Elias att ta resten. 4 stenar är kvar. Om Elias tar nu 2 tar Andreas en sten och vinner, om Elias tar 1 eller 3 (av 4) tar Andreas resten och vinner i alla fall.
15 stenar i högen:
Andreas tar 6 stenar och lämnar 9 kvar vilket är ett hopplöst läge för Elias eftersom om han nu tar en sten så blir det 8 kvar och Andreas vinner genom att ta 4 som i fallet ovan. Tar Elias fler an en sten så blir det inte fler än 7 kvar och Andreas kan ta resten på en gång och vinna.
20 stenar i högen:
Andreas tar 3 stenar och lämnar Elias med 17, ett hopplöst läge för Elias igen. Om Elias tar 1, 2, 3, 5, 6 eller 7 stenar så kan Andreas se till att nästa gång blir 9 stenar kvar för Elias. Tar Elias 4 så blir det 13 kvar och Andreas tar 2 (11 kvar), Elias 1 (10 kvar), Andreas 5 (5 kvar) och vinner.
Börjar Andreas på ett annat sätt så kan han förlora. Tänk, hur du i Elias ställe skulle spela och vinna om Andreas tog ett annat antal stenar än 4 av 8 eller annat än 6 av 15 eller annat än 3 av 20.
Lösning på problem 3
Svar: 16.
I omgång två adderar man 1 till alla tal vilkas ordningsnummer i raden är en multipel av 2 och allmänt: i omgång nr k ökas med 1 alla tal vilkas ordningsnummer i raden är en multipel av k. Talet som står på plats 120 ökar med 1 i varje omgång med nummer som är delare till 120. Efter 200 omgångar blir talet nr 120 (som från början var 0) lika stor som antalet positiva heltalsdelare till 120.
Kan man beräkna hur många (positiva heltals-) delare har talet 120 så har man löst problemet. Att testa alla tal från 1 till 200, vilka som är delare till 120 kan vara jobbigt. Det finns smartare metoder.
Metod 1: Om produkten av två naturliga tal är 120 så är ett av talen mindre än 11 och ett, större än 11, så det räcker med att lista alla delare till 120 som är mindre än 11. De är: 1, 2, 3, 4, 5, 6, 8 och 10. Åtta delare. De som är större än 11 är lika många, så sammanlagt är de 16.
120=1∙120=2∙60=3∙40=4∙30=5∙24=6∙20=8∙15=10∙12
Metod 2: Primtalsfaktoruppdela 120 (Vera gjorde det med hjälp av ett primtalsträd.) 120=2∙2∙2∙3∙5.
Varje delare till 120 kan enbart vara en multipel till något eller några av de tre primtal som är delare till 120, alltså: 2, 3 och 5 och inga andra. Tvåan kan förekomma högst i tredje potens i en delare till 120, trean och femman bara i första potens eller inte alls, alltså 0 till 3 tvåor, en eller ingen trea och en eller ingen femma, 4∙2∙2 möjligheter. Här listas de alla:

Det första talet i listan är 1 som kan sägas vara en produkt av inga faktorer alls, det sista är 120.
Innehåll: LR
