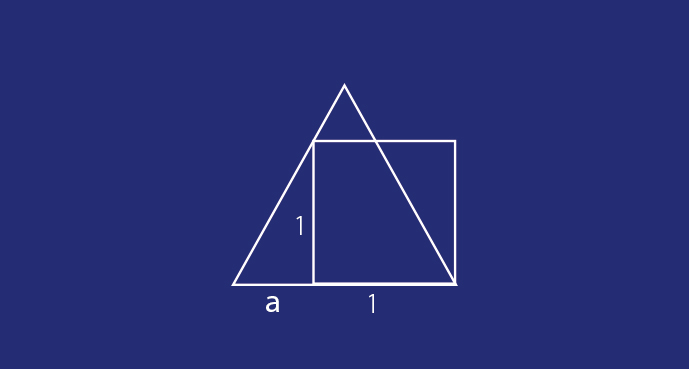
Svar: Den liksidiga triangeln är störst, omkretsen är \(3 + \sqrt{3}\).
Lösning: Använd laborativt material för att lösa problemet men då blir det såklart inget exakt svar på hur stor triangelns omkrets är jämfört med kvadraten.
För exakt lösning: Kvadraten avskär en halv liksidig triangel. Eftersom kvadratens sida är 1 så är den ena katetens längd 1. Låt den andra kateten ha längden a. Då är \(\tan 60^\circ = \frac{1}{a}\) med lösning \(a = \frac{1}{\sqrt{3}}\). Den liksidiga triangelns omkrets är \(3(1+a)=3\left(1+\frac{1}{\sqrt{3}}\right)=3+\sqrt{3}\) . En lösning utan att använda trigonometri bygger på den välkända relationen mellan sidorna i en halverad liksidig triangel.

Tillbaka till adventskalendern.