- I maj kommenterade Samia Talbi på Lernia en föregångare till problem 3.
Under oktober månad svarade följande på månadens problem.
Mattegruppen på Käppala skola, Lidingö: Jesper, Jonatan, Sarah, Edvin, Lukas, Felix, Oscar, Matilda, Alexandra, Emma, Saga (lärare: Jessica John)
Grönkullaskolans årskurs 4, Alvesta (Lärare: Viktoria Lundström)
Malin L och Anna S, Filip B, Linus T och Filip S – 13-åringar som läser spetsmatte i Stenungskolan i Stenungsund
och i samma skola Rasmus, Viktoria, Jack och Isak – spetsmatte i årskurs 9.
Patrik och andra i 3-4 Lila i Grossbolsskolan i Forshaga kommun (lärare: Mari Lindström )
Viktor, Sebastian, Filip P samt Isabelle E, Dalia G, Eric S, Elin P, Mohammed H, och Amanda K i klass 9B och två som glömde skriva sina namn i Dala Södra (högstadieskola), Bromölla. (lärare: Katrin)
Max i Vallkärra skola i Lund
David M (med sin mamma), elev i 3A i Långmosseskolan, Angered
En elev i årskurs 7 i Korsholms högstadium, Finland (lärare: Emma Sjöström)

Lösning på problem 1
Svar: 7 (eller kanske -7, ”minus sju”)
Flera nämner baklängesmetoden. ”Man får räkna motsatta räknesätt än vad som står i texten. T ex så avslutar man med att multiplicera med 5 och får 2015. Då börjar vi istället med att dividera 2015 med 5.” – skriver Käppalaskolans elever.
2015/5 = 403
403–3 = 400
400/8= 50
50–1=49
√49 = 7
David ställer upp en ekvation:
((x ∙ x + 1) ∙ 8 + 3) ∙ 5 = 2015
och löser den steg för steg baklänges dvs från höger till vänster:
((x ∙ x + 1) ∙ 8 + 3) ∙ 5 = 2015
dela med 5
(x ∙ x + 1) ∙ 8 + 3 = 403
minska med 3
(x ∙ x + 1) ∙ 8 = 400
dela med 8
x ∙ x + 1 = 50
minska med 1
x ∙ x = 49
Talet som vi hade från början var 7 eftersom 7 ∙ 7 = 49
Även de som inte förklarade räknade på samma sätt och kom fram till 7.
(Vi, som har lärt oss om negativa tal, vet att även (-7) ∙ (-7) = 49, så kanske började vi med 7, kanske med -7.)

Lösning på problem 2
Svar: Draken hade 29 huvuden när riddaren flydde.
Dalia i Dala Södra skriver:
”Draken hade från början 5 huvuden. Riddaren högg först av alla 5 av drakens huvud. För varje avhugget huvud växte det ut 5 st i dess ställe. Det blir 25. Riddaren hög nu av ett av dessa 25 huvud, då blev det 24. Men i dess ställe växte det ut 5 huvuden. Då blev det 29 huvuden totalt.”
Ungefär likadant beskriver 13-åringarna i Stenungsund händelsen. Beräkningen blir alltså 5 + 5 + 5 + 5 + 5 – 1 + 5 = 29.
(Med så många huvuden skulle draken kunna lösa alla problem samtidigt i en kängurutävling.)
De flesta verkar ha utgått ifrån att riddaren högg av drakens fem ursprungliga huvuden först innan han tog sig an de nya. Men det står att nya huvuden växte ut omedelbart, så han kunde göra på olika sätt. Det spelar ingen roll vilka av drakens huvuden ridaren högg av eller i vilken ordning. För den som inte tycker att det är så självklart förklarar vi så här:
För varje avhuggning ökade antalet huvuden på draken med 4. Draken hade 5 huvuden i början, så efter 6 avhuggningar hade den 5 + 6 ∙ 4 = 29 huvuden. Niorna i Stenungsund räknar på detta sätt. De har skrivit en generell formel: 5 + 4N. Nu kan riddaren huga av hur många huvuden som helst, man sätter in antalet avhuggna huvuden för N i formeln och får som resultat antalet huvuden som draken har kvar.
Till slut en detalj ur Malin och Annas lösning: en ledsen drake med ett enda huvud.


Lösning på problem 3
Svar: 36 (De utvalda talen var 15 och 21.)
Triangeltal
Det första steget till att lösa problemet måste rimligen vara, att beräkna summan 1 + 2 + 3 + … + 26.
David kopplar 1 med 26, 2 med 25, 3 med 24 osv och får tretton talpar med summan 27 i varje. Så summan av alla är 13 ∙ 27 = 351. Summa av heltal från 1 till n kallas triangeltal och betecknas Tn alltså T26 = 351 och den allmänna formeln är Tn = n ∙ (n + 1) / 2.
Testmetoden
Elever som klarade det första steget fortsatte nog med att testa olika talpar och kom alldeles riktigt fram till att talen, som man valde ut (låt oss kalla dem a och b med a > b) var 15 och 21.
Testar man planlöst kan det behövas många tester innan man hittar just dessa två tal.
Innan Amanda börjar testa, subtraherar hon de två största talen (25 och 26) från 351 och visar att produkten a ∙ b måste vara minst 300. Då vet man att det minsta av dessa två tal måste vara större än 11 därför att 11 ∙ 26 < 300.
Om a = 12 så är 12 ∙ b + 12 + b = 351 alltså 13 ∙ b + 12 = 351 alltså 13 ∙ b = 339 men 339 är inte jämt delbart med 13.
Om a = 13 så är 13 ∙ b + 13 + b = 351 alltså 14 ∙ b + 13 = 351 alltså 13 ∙ b = 338 men 338 är inte jämt delbart med 14.
Samma sak med a = 14 men med a = 15 funkar det: (15 + 1) ∙ b = 336 ger b = 21 och a + b = 36. EUREKA!!
För att förvissa oss om att det inte finns fler lösningar testar vi även för a = 16. Ju större a desto mindre b och när vi testar för a = 17 ser vi att b inte länge kan vara större än a.
Faktoruppdelning
En lösning som Samia Talbi på Lernia skickade till oss i maj.
Vi utgår från att summan av alla 26 tal är 351 och eftersom produkten av a och b är lika med summan av alla andra får vi då att a + b + a ∙ b = 351.
Vidare:
b (1+a)+a=351
Jag började prova med ett värde för a och se vad b blir. Snart insåg jag att eftersom b måste vara ett heltal så skulle det hjälpa vidare att uttrycka b som funktion av a och använda delbarhet.
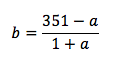
Hittills är det dock svårt att använda delbarheten då a dyker upp i täljaren och nämnaren. Men om man ser till att neutralisera a i täljaren har vi bara en enda a-term kvar att resonera på.
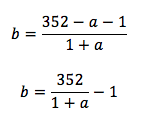
Nu återstår att leta efter ett a som gör att a + 1 blir en delare av 352 = 25 ∙ 11
a + 1 = 11 ger ett b över 26, men nästa möjlighet a + 1 = 2 ∙ 11 = 22 ger den acceptabla lösningen b = 15. Andra a går ej då blir de större än 26.
Alltså blir summan 21 + 15 = 36
En lösning till, som använder faktoruppdelning av 352.
a ∙ b = 351 – a – b
a ∙ b + a + b = 351
a ∙ b + a + b + 1 = 352
(a + 1) ∙ (b + 1) = 352
Vi vet att a och b ligger inom intervaller 1 … 26 alltså a + 1 och b + 1 ligger inom 2 … 27 och den enda uppdelningen av 352 i två faktorer som uppfyller villkoret är, som Samia har visat, 16 ∙ 22. Alltså a + 1 = 16 och b + 1 = 22 och därmeda = 15, b = 21 och a + b = 36.
Finns det någon regel?
Elin och Erik i 9B i Dalaskolan Södra försökte upptäcka en bakomliggande princip i de svar som de fick fram. Ett samband som vi redan har bevisat är (a + 1) ∙ (b + 1) = 352 och nu kan vi enkelt bevisa att om vi i problemet ersätter 26 med ett annat naturligt tal n och a och b är lösningen, så gäller (a + 1) ∙ (b + 1) =Tn+1.
Elin upptäckte att i talraden 1 till 26 fanns lika många tal mellan 15 och 21 som efter 21.
Erik märkte att de flesta inblandade tal (351, 21, 15, 315) är delbara med 3.
En tredje märklighet är att talen 351, 21, 15, 36 (som är 21 + 15) och 6 (som är 21 – 15), alla är triangeltal: 351 = 1 + 2 + … + 26, 21 = 1 + 2 + 3 + 4 + 5 + 6, 15 = 1 + 2 + 3 + 4 + 5, 36 = 1 + 2 + … + 8, 6 = 1 + 2 + 3.
Kan det vara slumpen eller ligger det något i det? Eller kanske problemkonstruktören valde talet 26 just därför att det var så speciellt?
Ersätter man 26 med andra naturliga tal, så visar det sig att ibland finns det en lösning, ibland ingen, ibland flera. Men 26 = 52 + 1. Försök att ersätta 26 med andra tal av formen k2 + 1: 10, 17, 37, 50, 65, … och lösa de nya problemen. Hittar ni svaren? Följer de några regler?
Innehåll: LR
