- Lösningar har kommit från:
Några elever ur en 7-9:a i Magelungens skola i Södertälje (lärare: Lena Jönsson)
Avi, Marcus, Oskar, Jonathan, Daniel, Olle, Alice, Saga, Elsa, Mira och Laura i 6K och 6L på Junkaremålsskolan i Tranås (lärare: Jessica Pihl)
Emil J i klass 3B i Östermalmskolan, Stockholm
Albana M i Korallensfriskola
Thelma H och Vilma M i 7:an på Åsenskolan
Amil M i klass 3A på Krokslättsskolan i Mölndal
Lösning på problem 1
Svar: För den ursprungliga bilden gällde B som det rätta svaret men det visade sig vara svårt att behålla korrekta proportioner på vår webbsida och att få bilden att se likadan ut på alla datorer. ”Skalan blev fel” – skriver Daniel och Olle i Junkaremålsskolan. Bilden blev mera långsmal eller mera kortbred än originalet.
De flesta har svarat B, andra har föreslagit bitar som föreföll passa bäst eller minst dåligt på deras bildskärmar eller pappersutskrifter.
Så här behandlade problemet Lena Jönsson och hennes elever i Magelungens skola:
Vi resonerade oss fram till att biten måste ha fyra hörn varav ett har en rät vinkel. Motstående hörn till hörnet med räta vinkeln ska ha en spetsig vinkel.
Den enda figur med dessa egenskaper är figur B. Men klipper man ut figur B och sätter in den i spegeln, så passar den inte. Så det rätta svaret borde vara att ingen bit passar in.
Men om det är tänkt att biten inte behöver täcka hela hålet så passar bit A in.
Svar: A eller ingen.
Lösning på problem 2
Svar: 10 cm
Emils lösning:
Om något varken är större eller mindre än x så är det x
alltså: kubens volym = rätblockens volym
alltså: rätblock etts volym är samma som rätblock två och tres volym
Om jag räknar ut rätblock etts volym så har jag rätblock två och tres volym med:
1 cm ∙ 10 cm ∙ 100 cm = 1000 cm3
kubens volym = 1000 cm3
3√(1000 cm3) = 10 cm
Kantlängd: 10 cm
Helt korrekt! Varje rätblock har volym lika stor som kubens volym, så det räcker att beräkna volym av ett av dem. Men det var inte heller fel att beräkna alla tre rätblockens volymer, som de flesta andra gjorde, för att försäkra sig om att det stämde.
Lösning på problem 3
Svar: 641
Alba skriver bara: 625 + 16 = 641 Varifrån kommer det?
Mira och Laura provade att dela 10000 med olika tal på miniräknaren och fick 10000/16 = 625.
Då har vi en förklarning till Albas svar. 641 är alltså en möjlig summa av a och b.
Men om vi undrar om det finns fler lösningar, hur ska vi gå till väga för att undersöka detta? Att dela 10000 med alla tal upp till 9999 är alltför jobbigt. Det minsta av talen a och b kan inte vara större än 100, så det räcker med att dela 10000 med alla positiva heltaltal upp till 100. Tar vi bort de som är jämnt delbara med 10 så återstår bara 90 divisioner. Fortfarande ganska jobbigt.
Elever i Magelungensskola faktoriserade 10000 i ett primtalsträd:
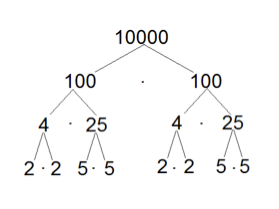
och det visade sig att 10000 är produkten av fyra tvåor och fyra femmor, 10000 = 2∙2∙2∙2∙5∙5∙5∙5.
Primfaktorerna 2 och 5 kan sägas vara de minimala faktorerna till 10000 eftersom ingen av dem är en produkt av två ännu mindre faktorer. Man kan gå till väga på olika sätt när man faktoriserar ett tal, t ex 10000 = 10∙10∙10∙10 = 2∙5∙2∙5∙2∙5∙2∙5 = 2∙2∙2∙2∙5∙5∙5∙5
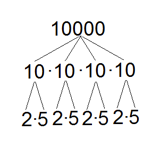
men aritmetikens fundamentalsats säger att ett tal alltid ger samma uppsättning av primtal på slutet. Av detta följer av att talen a och b som är faktorer till 10000, måste vara ettor eller produkter av tvåor och femmor, fyra tvåor sammanlagt och fyra femmor. Vill man inte att något av talen a och b ska vara delbart med 10 så det enda sättet är att fördela primtalsfaktorerna så, att alla tvåor hamnar i ett tal och alla femmor i det andra, (Det spelar ingen roll vilket av talen heter a och vilket heter b.)
2∙2∙2∙2 + 5∙5∙5∙5 = 16 + 625 = 641 är den enda möjliga lösningen.
Innehåll: LR
