- Lösningar har kommit från:
Josefine L. i 7:an på Framtidskompassen, V. Ingelstad.
Jonathan E. Wilma P., Alina S., Wilma T. och Fredrik i 6A, Rasmus K., Nora L.M. och Alexander N. i 6B samt Isa W. och Estelle F. i 6D på Hemmestaskolan.
Amitis och Elliot i klass 3B på Töjnaskolan, Sollentuna.
Hampus M. och Hussein A. i årskurs 9, Rasmus N. i 8a samt Simon Ö., Albin N., Celina O. och Elin H. i 7a på Hästveda skola, Hässleholms kommun (lärare Caroline Hansson).
Klass 3-4 lila på Grossbolsskolan, Forshaga.
Vera P. i 6H på Vasa Real, Stockholm.
Eleverna i klass 1 på Björbo skola (lärare Sara Lindfeldt).
Lösning på problem 1
Svar: Anna står närmast Bob.
Sara L.: Eleverna kom snabbt fram till att det var Jan eller Anna som var närmast. Sedan började de att prova sig fram för att bestämma vilken. De ritade, streck och ringar. En elev gjorde ”ringar”(cirklar) för att se hur många det fick plats. Kompisen kom då ganska snabbt på att det inte gick att göra så eftersom ringarna blev olika stora. De använde sedan fingrar, sudd, pennor och annat material för att försöka mäta. Slutligen insåg de att de behövde en linjal att mäta med.

Kanske mätte eleverna avstånden mellan utskrifter av namn i stället för mellan kryssen som markerar positioner?
Även äldre elever mätte med linjal, andra förstod att med ”ring” menas det som inom geometrin kallas ”cirkel” och dess ”mitt” är cirkelns medelpunkt. Josefine, Vera, Fredrik, Simon och Albin förklarar att Anna står närmast Bob därför att det är bara hon, förutom Bob själv, som står inne i cirkeln/ringen.
Bob står i cirkelns medelpunkt. Varje cirkel har en radie, som man brukar beteckna med bokstaven r. Alla punkter på en cirkel befinner sig på avståndet r från cirkelns medelpunkt. Jan och Mia står på själva cirkeln, de står på avståndet r från Bob. Siv och Per står utanför cirkeln, de står på avstånd större än r. Anna inne i cirkeln har avståndet mindre än r till medelpunkten och Bob.
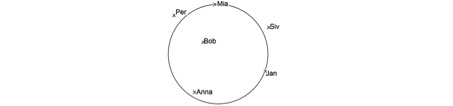
Skulle inte Bob stå mitt i ringen, så skulle det inte vara säkert att Anna skulle stå närmast Bob, i figuren ovan är det Per som står närmast Bob.
Lösning på problem 2
Svar: Ja det är möjligt och då ska kortet med bokstaven ”R” ligga kvar i låda 2.
Det finns två sätt att tänka:
Metod 1: Peter får bara plocka bort korten från lådorna, han får inte lägga in nya. Men i varje låda ska ett kort finnas kvar. När kortet ”V” ligger ensamt i låda 4, vet vi att det är detta kort som ska finnas kvar där till slutet. Vi vet också att det ska bli olika bokstäver i olika lådor, så något kort med ”V” får inte ligga i någon av de övriga lådorna när Peter är klar. Vi plockar bort dem.
Har vi bara en bild i stället för riktiga lådor och kort, så kryssar vi över korten.
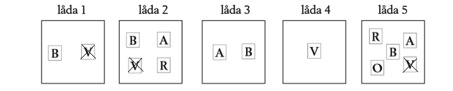
Nu finns B ensamt i låda 1, då stryker vi bort alla ”B” i de övriga lådorna. Vi fortsätter på samma sätt: ”A” ensam i låda 3 och när An stryks blir ”R” ensam i låda 2 och till slut har vi ett kort kvar i varje låda, varje med en annan bokstav.
Metod 2: Det finns fem bokstäver och fem lådor och i varje låda ska det finnas en annan bokstav kvar. Då måste alla fem bokstäver vara med. ”O” finns bara i låda 5, då måste det vara kvar där och de övriga kort från låda 5 ska plockas bort. Vi stryker dem.

Nu finns ”R” endast i låda 2. Vi stryker de övriga kort (”B”, ”A” och ”V”) i låda 2. Då finns ”A” endast i låda 3. Fortsätter vi så, så strax finns det bara ett kort kvar i varje låda. Varje kort med en annan bokstav. Det blir samma kort som i metod 1, det finns nämligen bara en möjlig uppsättning.
Josefine, Vera, Klass 3-4 lila på Grossbolsskolan, elever i Hemmestaskolan m.fl. löste problemet med metod 1. Rasmus i Hästvedaskola började som i metod 2 och sedan fortsatte som i metod 1:
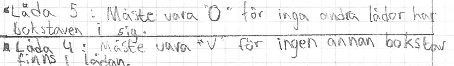
o.s.v. – även det fungerade bra. I lite svårare problem, som t.ex. när man löser sudoku, måste man kombinera flera metoder för att nå lösningen.
Sara L. : Jag hade gjort i ordning 5 ”lådor” som eleverna fick plocka med. När de kom på tänket var det snabbt löst. De var mycket stolta över sin förmåga att lösa problemen och märkte att de kunde mycket mer än de först trodde.

Många har märkt att bokstäver som blir kvar bildar ordet ”BRAVO”.
BRAVO till alla som klarade problemet!
Lösning på problem 2
Flera svarande använde 6 linjer, några behövde fler men Josefine och Vera klarade det med bara 5 linjer. Här ser vi deras bilder, alla vinklar markerade på Josefins bild:
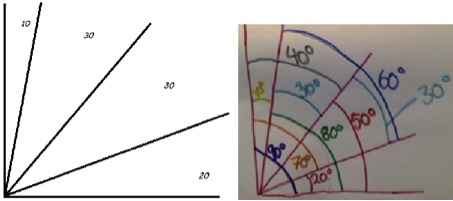
Vera påpeckar att det finns fler ”lösningar”. Ja, här kommer några.
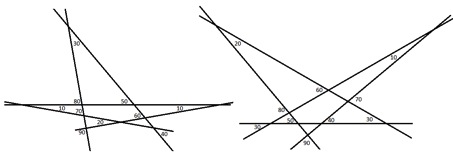
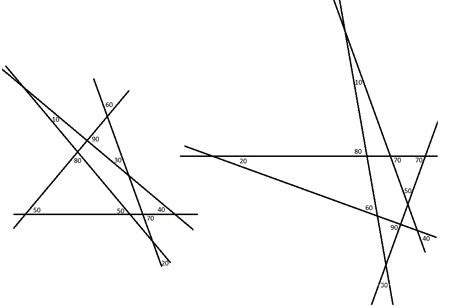
I Josefins och Veras figurer korsas alla linjer i en punkt, vi har valt att göra tvärtom, varje par av linjer har en egen skärningspunkt. Linjerna i varje av figurer ovan korsar varandra i tio punkter. En av de begärda vinklarna förekommer vid två korsninspunkter övriga vid en. Figuren uppe, till höger, vissar inte ett riktigt nytt system av linjer, man får den genom att vrida 50° medurs och parallellförflytta varje linje i Veras eller Josefins figur. Det finns faktiskt ytterliggare fyra väsentligen olika system av fem linjer.
Problemets fråga var ”Hur många linjer minst måste man rita?”. Vera och Josefin har vissat att fem linjer räcker. ”Fem” är ett rätt svar om fem är det minsta möjliga antalet, dvs, att det inte går att göra så med fyra eller färre än fyra linjer. Så här kan vi bevisa det:
När två linjer korsas så bildas det fyra vinklar, antingen fyra räta vinklar eller två lika stora spetsiga och två lika stora trubbiga. Så ett par linjer bidrar med bara en vinkelstorlek som är mindre eller lika med 90°. Bland fyra linjer finns sex par, alltså de kan bilda som mest sex olika stora vinklar som är mindre eller lika med 90°. I problemet krävs det nio olika sådana viklar, alltså fyra linjer räcker inte. Med ännu färre linjer blir det naturligvis inte fler vinklar.
Innehåll: LR
