Det har kommit svar och kommentarer från:
- Linnea D. Linnéa B. och Arvid W., elever på Mosstorpskolan Skärblacka, årskurs 8.
- Vera P.4a, Lilla Adolf Fredrik Stockholm
- Madelene H. m.fl. i klass 9c i Centralskolan Töreboda (läraren: Markku Julin)
- Myra H. och Jacob T., Höglandsskolan klass 6B (Lärare: Marie Bevegård)
- Karl Emil W. och Alexander B. klass 4c, Fastebolskolan (Lärare: Ylva-Li Feuk Kalldin)
- William S., Melvin J. Isabelle S., Ida P. och Alma F— matematikälskarna i Västra Alstad (lärare: Sofie Palm)
- Elever i skolår 3 på Hallenskolan i Kållered löser månadens problem på sin klassblogg (lärare: Fredrik Melleroth)
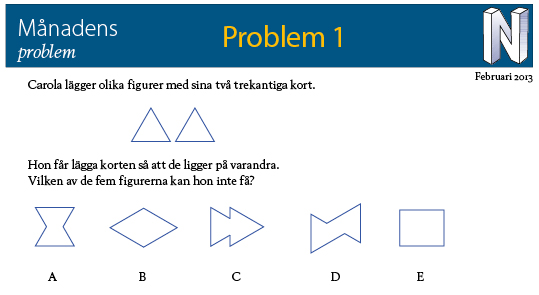
Svar: E. Hon kan inte lägga rektangeln.
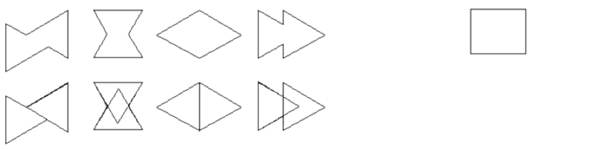
Det är enkelt att få de första fyra figurerna men rektangeln är omöjlig.
Två sidor i en rektangel är antingen parallella eller vinkelrätta mot varandra men ingen av Carolas kort har parallella eller vinkelrätta kanter, så rektangelns fyra sidor måste göras av kanter från fyra olika kort. Två räcker inte.

Här ser vi ett försök att bygga en rektangel av två kort. Det blev bara två sidor. Sedan kommer en kvadrat av fyra kort och sist en mera avlång rektangel av sex kort.

Svar: De startar med 3. Peter adderar 2 så det blir 5. John multiplicerar med 3 och får 15. När sedan Niklas subtraherar med 1 så hamnar resultatet på 14.
Uträkningen kan skrivas så: (3+2)*3 – 1= 14
Det är parentesen som säger, att 2 ska adderas först och därefter ska summan multipliceras med 3. Den är nödvändig trots att plus står före gånger.
14 är det största möjliga resultatet. Skulle pojkarna agera i omvänd ordning så skulle de få det minsta möjliga resultatet: (3-1)*3+2= 8.
Testa med andra tal. Hur får man det största och hur det minsta resultatet?

Svar: Det går inte med 16 stickor men en triangel med sidorna av 4, 5 och 6 stickor (15 sammanlagt) är spetsvinklig och inte likbent. 15 är också det minsta antalet stickor för vilket det går.
Problemet handlar om stickor men är egentligen inte i första hand ett problem för barn. I en gymnasiebok skulle man kanske fråga: Finns det en spetsvinklig men inte likbent triangel med omkrets 16 i vilken alla sidolängder är heltal? Vilken är det minsta möjliga tal n för vilket det finns en spetsvinklig men inte likbent triangel vars sidolängder är heltal och omkrets är n?
Är detta för svårt så hoppa över till avsnittet ”Andra metoder”.
När en triangel med sidolängder a, b och c inte är likbent så är a, b och c tre olika tal som uppfyller triangelolikheter a < b + c, b < a + c och c < a + b. (Vet man att c är störst, så räcker att testa c < a + b.)
Men vår triangel ska också vara spetsvinklig och det har ingen av svarande klarat. Några visste vilka trianglar som var rättvinkliga och då var ni hälften på vägen till att klara det.
Pythagoras sats kan uttryckas så: Om a, b och c är längder av triangelsidor och vinkeln mittemot sidan med längden c är en rät vinkel, så a²+b²=c². Även det omvända gäller: om a²+b²=c² så är vinkeln mittemot sidan c en rät vinkel.
Ju kortare en sida i en triangel är desto mindre vinkeln mittemot så länge de övriga sidolängder inte ändras och ju mindre c desto mindre c² för c>0. Därför gäller i en spetsvinklig triangel: a²+b²>c². Alltså man kan säga att kvadrater av sidolängder i en spetsvinklig triangel uppfyller triangelolikheter.
Vi betraktar trianglar med heltalssidor och omkretsar upp till 16. På grund av triangelolikheten kan ingen sida i en sådan triangel vara större än 7. Möjliga sidolängder är alltså 1, 2, 3, 4, 5, 6 och 7 och deras kvadrater är 1 4 9 16 25 36 49. För att få en spetsvinklig triangel behöver vi ur den sista listan tre tal som uppfyller triangelolikheten. För att triangeln dessutom inte ska vara likbent måste de vara tre olika sådana. Det finns bara 3 möjligheter: 16, 25 och 36, 16, 36 och 49, eller 25 36 och 49. Det betyder att triangeln har sidolängder 4,5 och 6 eller 5, 6 och 7. Den första har omkretsen 15, de andra mera än 16. Alltså 15, som är den ända upp till 16, är den minsta möjliga omkretsen och en triangel medomkretsen 16 som uppfyller villkor finns inte.
Andra metoder att se om en triangel är spetsvinklig
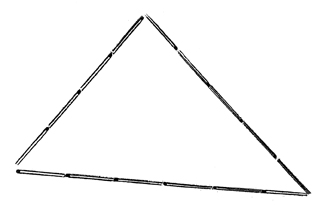
Flera svarande trodde att triangeln med sidorna 2, 3 och 4 uppfyllde villkoren.

Lägger man 9 lika långa stickor så här på bordet så ser man direkt, att den inte är spetsvinklig.
För trianglar med sidolängder 4, 5 och 6 är det lite svårare att avgöra.
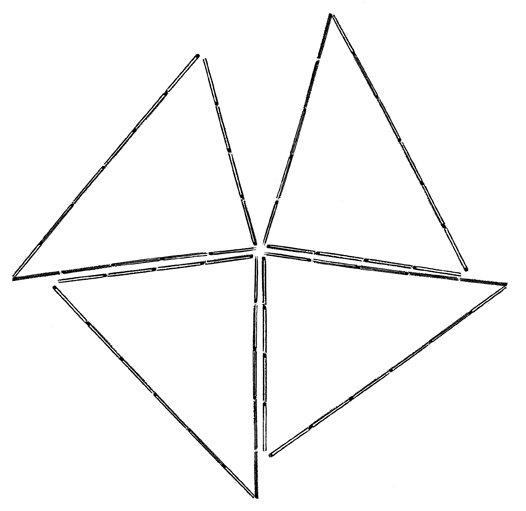
Men om vi lägger fyra sådana trianglar med de största vinklarna intill varandra, så ser vi att fyra sådana vinklar tillsammans är lite mindre än 360° alltså är den största vinkeln spetsig. Ja, det var den sökta triangeln.
Vet du själv flera metoder?
Triangeln med sidolängder 3, 6 och 7 testar vi på ett annat sätt:

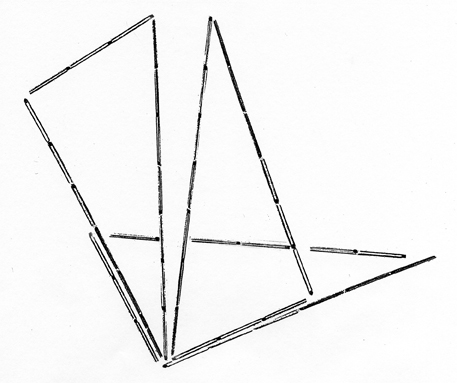
Två stickor i den längsta sidan i en av trianglarna är borttagna för att ge plats åt de två övriga trianglarna
En vinkel i triangeln är större än de två övriga tillsammans. Då måste den största vinkeln vara trubbig.
Nu en metod som använder randvinkelsatsen:
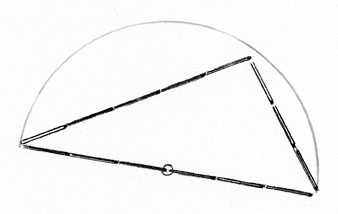
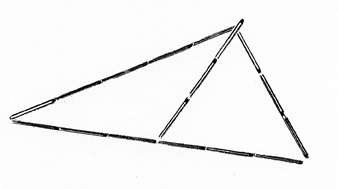
Man ritar en halvcirkel med triangelns längsta sida som diameter. Skulle motstående hörnet ligga på randen, så skulle vinkeln vara rätt. Skulle den ligga utanför cirkeln så skulle vinkeln vara spetsig. Men nu ligger den innanför, alltså är den trubbig. I stället för att rita halvcirkeln kan vi göra en extra radie av tre stickor. Sticker den ut genom hörnet, så är triangeln trubbvinklig.
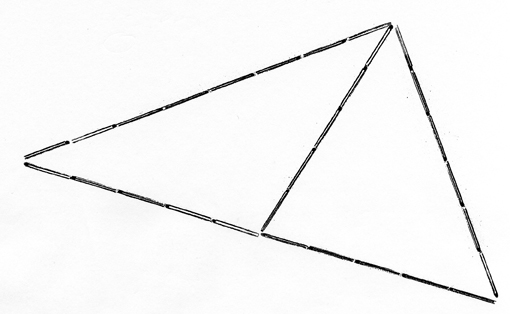
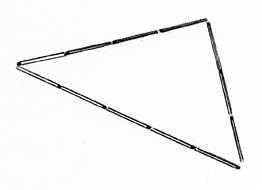
I triangeln med sidolängder 6, 8 och 10 är radien av den omskrivna cirkeln 5 och den når precis till motstående hörn. Alltså är triangeln rättvinklig. Triangeln med sidorna 3, 4 och 5 behöver vi inte testa, den har alla sidor hälften så stora som den förra, så vinklarna måste vara lika stora.
Till slut en extra fråga att fundera på tills svaren på marsproblem kommer:
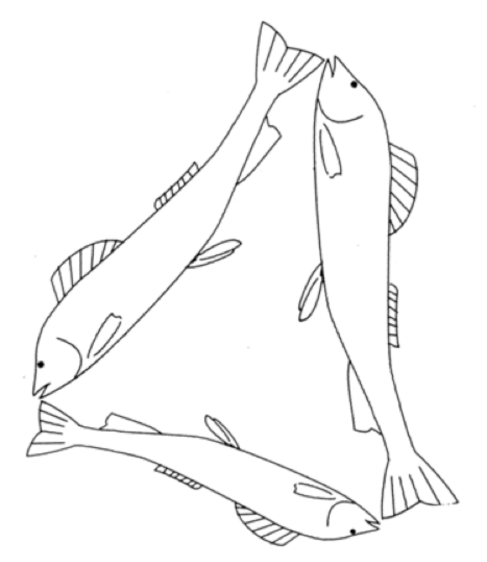
Tre likformiga fiskar bildar en spetsvinklig triangel. Vilken area är störst – den största fiskens eller de övriga två andras tillsammans?
/Leo
Innehåll: LR
