Vi hade två ganska lätta problem i oktober och som väntat kom många bra svar. Problem nr 3 brukar vara det svåraste. Den här gången var det ett problem som inte bara krävde att man tänkte själv utan också att man satte sig in i hur andra tänker. Många gav rätta svar även på det sista problemet och flera förklarade hur de resonerade.
Det har kommit svar och lösningar från:
Joel och David B., Tom A. och Amanda L., Amanda H. och Lisa, Sara D., Alexandra D., Valter G. Hulda J. samt Gustav N. och Daniel L. i spetsklasen i Roggeskolan
Joakim S. och Magnus L., Maryam M. samt Anna H. och Jacob T. i Kunskapsskolan i Örebro
Rasmus E. och andra i klass 4c på Mosseleskolan i Värnamo
Emma S. i 7b i Framtidskompassen AB i Västra Ingelstad
Edvin J. i kl. 7b; Jonathan K. i klass 7B på Almby Skola i Örebro
Julia och Linnea samt Viktor K. från Alfred Dalinskolan i Huskvarna
Pontus K., Arvid W., Linnea B., Linnea D. och en anonymmus i Mosstorpsskolan i Skärblacka
8-åriga Caroline J. som gav rätta svar på alla 3 problem
Victor L. i Enehagens skola i Värnamo
Vera P. i 4a i Lilla Adolf Fredrik Skola i Stockholm
Rasmus N. i klass 6a, Hästveda skola
Lovisa J. och Gaia I., Simon T. och Klas S., Erik H. och Maciek W. samt Kevin H., Philip G. och David H. i årskurs 8 och 9 i Storavallaskolan i Degerfors
MArcin W i klass 7, Helenaskolan i Skövde.

Svar: 48 cm
Lösningsmetod 1
Den vanligaste metoden var att beräkna kvadratens sida, 8cm/4=2cm, rita rektangeln med sidorna 15cm och 9cm, rita in kvadraterna i rektangelns alla hörn och beräkna längder på alla sidor i den figur (en tolvhörning) som bildas när man skär bort kvadraterna.
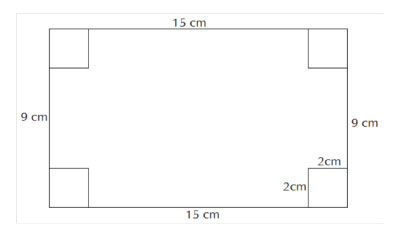
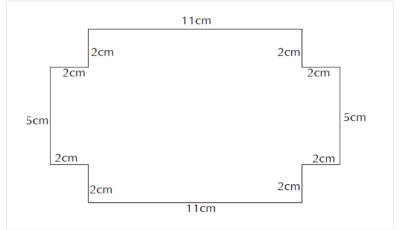
Därefter beräknar man figurens omkrets genom att summera alla dessa sidor, 2*11cm + 2*5cm + 8*2cm=48cm.
Lösningsmetod 2
Många påpekade att omkretsen inte förändras när man skär bort kvadrater från rektangelns hörn, så det skulle räcka med att bara beräkna den ursprungliga rektangelns omkrets. Men de tyckte kanske att det var jobbigt att förklara varför det är så och valde att göra alla beräkningar som i metod 1.
Emma S. satsade på en bra förklaring (här något ändrat): ”Sidan på kvadraterna som tas bort är 2 cm, men det påverkar inte figurens omkrets då ”yttersidorna” (de röda i figuren nedan) på kvadraterna som tas bort från omkretsen har samma längd som ”innersidorna” (de gröna) som nu blir en del av omkretsen istället.”
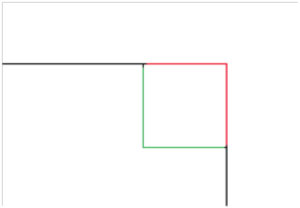
Mera allmänt:
Vera P. påpekar att ”Omkretsen blir likadan oavsett hur stora kvadraterna man tar bort ifrån hörnen är.” – Det är riktigt. Vi skulle kunna lösa problemet även om vi inte visste kvadraternas omkretsar och svaret skulle bli detsamma. Några intressanta frågor som dyker upp: Hur kan man ändra formen på en geometrisk figur utan att omkretsen förändras? … utan att arean förändras? … eller så att varken omkretsen eller arean förändras? Kan man göra så med vilken figur som helst?

Svar: 22
Lösningsmetod 1
Så här presenterar Julia och Linnea sin lösning.
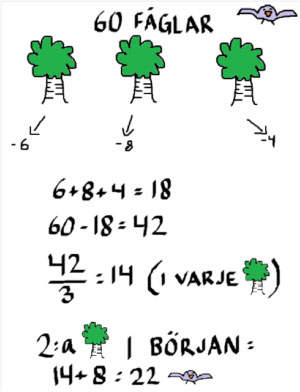
Emma återger samma tankegång med ord:
Det flög bort totalt 18 fåglar. Kvar är då 42 fåglar. I varje träd satt då 42 / 3 = 14 fåglar (lika många i varje träd).
Nu räknar vi baklänges:
Träd 1: 14 + 6 = 20
Träd 2: 14 + 8 = 22
Träd 3: 14 + 4 = 18
Kontroll: 20 + 22 + 18 = 60
Lösningsmetod 2
Gustav N. och Daniel L. tänkte annorlunda.
” – Jag jämnade ut det för att 8 är 4 större än 4 så tog jag 22-8=14 och 18-4= 14 och på samma sätt tog jag 20-6 = 14”. Tankegången bakom ”Jag jämnade ut det” var nog densamma som i följande lösning:
Det flög 6 fåglar i snitt från varje träd, två fler än snittet från det andra och 2 färre från det tredje och det blev lika många kvar på varje träd. Det betyder att det från början satt två fler fåglar på det andra trädet än det snittet som gällde då, och eftersom snittet var i början 60/3= 20, så satt det 20+2=22 fåglar på det andra trädet.
För den som kan statistiska begrepp och vill räkna i huvudet är detta nog den smartaste metoden. Tänk på att ”6 fåglar i snitt från varje träd” betyder inte ”6 fåglar från varje träd”, utan att medelvärdet av fåglar från dessa tre träd var 6.

Svar: på onsdag
Några tyckte att det saknades uppgifter i problemtexten och därför gick det inte att lösa. Ha, ha! Det var meningen att man skulle tro det, nyckeln till lösningen finns men är väl dold. Det gäller att tänka på, hur Kent och Lina tänker.
Lösning
Skulle Lina eller Kent spela på måndag eller på fredag så skulle den som fick reda på sin speltid veta när den andre skulle spela, på tisdag respektive torsdag. Ingen av dem visste det, alltså ska matcherna spelas antingen på tisdag/onsdag eller på onsdag/torsdag. Skulle Lina spela på onsdag så skulle hon, även efter Kents svar, fortfarande inte veta om han skulle spela på tisdag eller på torsdag. Tydligen spelar Lina själv på tisdag eller på torsdag. Då vet hon att Kent ska spela på onsdag.
Observera att en fullständig lösning förklarar både hur Lina kunde lista ut Kents speldag och varför endast onsdag kunde vara det.
Fullständiga lösningar skickade: Joakim och Magnus; Vera; Gustav och Daniel samt Edvin J.
Här kommer ett intressant försök av Jonatan K.:
”Svar: På onsdagen. Eftersom Lina inte vet när Kent ska spela så kan hon inte spela på måndagen eller på fredagen. Av samma anledning kan Kent inte spela på måndagen eller på fredagen. Eftersom det bara finns tre möjliga dagar för Lina att spela på så hade han vetat när Lina skulle spela om han hade spelat på tisdagen eller torsdagen.”
Resonemanget håller inte riktigt ända fram. Vi vet att Lina undrar när Kent ska spela, och vi drar slutsatsen att Lina inte spelar på måndag eller på fredag. Men Kent visste inte det. När Lina frågar: ”Kent, vet du när du ska spela?” anar han kanske att Lina själv undrar det, men det framgår egentligen inte av Linas fråga. Kanske bekymrar hon sig bara om Kent fick och läste sitt meddelande.
Innehåll: LR
