Det har kommit svar och lösningar från Torpaskolan Vänersborg, elevens val, ma-avancerad,John O. som går i 5:e klass,
Sabine de R. i klass 7A på Nygårdsskolan i Göteborg,
Carl S. i 6C på Kullaviksskolan,
Oskar och Ida i 5f Fryxellskaskolan, Västerås samt från
förskollärare som deltagit i kursen ”Små barns matematik” i S:t Jörgens skola i Helsingborg ledd av Catrin Stensson.
På slutet har det även kommit lösningar från Christina, Elina, Samuel och Christoffer; Emma, Hanna, Charlie, Martin
och Melvin; Robin, C. H., Julia och Tobbe; Julia, Engla, Jesper och Jason; William, Anton, Victor och Elias samt Sara, Wilma, Hanna, Ariam och Johan, alla elever i klass 4-6 AB på Treälvsskolan i Lit, Östersund, Jämtland med läraren Mariah Sandström.

Svar: Mi
När Elin nuddade det sista trappsteget med en fot och sjöng: – Do, stod hon med andra foten ett trappsteg under. Sedan tog hon ett kliv bakåt och satte foten på trappsteget under det, alltså två trappsteg under det som hon nuddade. Samtidigt sjöng hon Do – igen. Sedan tog hon nästa kliv bakåt och sjöng – Ti – igen samtidigt som hon satte sin fot två trappsteg under det där hon sjöng – Ti – på vägen upp och så fortsatte hon. När hon sjöng – Mi – trampade hon trappsteget två trappsteg under det där hon sjöng – Mi – på vägen uppåt, alltså det knarrande trappsteget.
Elever i Torpaskolan i Vänersborg kom till samma svar:
”På tillbaka vägen blir det tonen MI som hamnar på det knarrande trappsteget.”
John O. och många andra svarar att ”Hon sjunger tonen: RE på det knarrande trappsteget på vägen ner.” och John förklarar det så här: ” När Elin kommer till det översta trappsteget sjunger hon den sista tonen. Sen tar hon ett steg bak, vilket innebär att hon börjar på det näst sista trappsteget.”
OK. Det finns olika sätt att gå, särskilt när man går baklänges nerför trappor men troligen beror dessa svar på att man har svårt att föreställa sig, hur det funkar när man går. Några använde bilder på trappan sedd från sidan, för att förklara hur de tänkte. Man ska komma ihåg att man använder två ben när man går. Det säkraste sättet att lösa problemet är nog att gå uppför och nerför en trappa och sjunga, men då är det viktigt att ha några vänner med som kan hjälpa på olika sätt. Ett annat sätt kan vara att rita trappan sedd framifrån och ”gå” på den med två fingrar.
Det finns många möjliga rätta svar på den andra frågan.
Elever i Torpaskolan föreslår:
”När man ska komma på DO på det knarrande, har vi kommit fram till att man går upp som vanligt och touchar bara översta trappsteget, backar ned två trappsteg, går upp ett trappsteg och sedan backar ned som vanligt.”
John skriver däremot: ” För att hon ska sjunga rätt ton på det sista trappsteget måste hon börja sjunga på det trappsteg hon slutade sjunga på!”
Och likadant tycker Sabine: ”Om hon säger ”Do” två gånger på det högsta trappsteget, kommer ”Do” på det knarrande steget.” (Alltså kliva på det sista trappsteget och börja skalan ner genom att ställa andra foten bredvid och sjunga Do och fortsätta ner med Ti La So Fa Mi Re Do.)
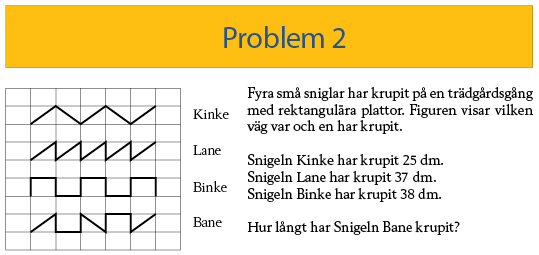
Svar: 35dm.
Här följer Torpaskolans lösning:
Snigel Kinkes sträcka består av diagonallinjer med en total längd på 25 dm. Så varje diagonal borde motsvara 25/5=5 dm.
Med den kunskapen går vi vidare till Lane vars sträcka består av 5 diagonala linjer och 4 lodräta linjer med en total längd av 37 dm. Då de diagonala linjerna motsvarar 25 dm borde de 4 lodräta linjerna bestå av den längd som återstår vilket är 37-25=12. 12/4=3 ger att en lodrät linje motsvarar en sträcka bestående av 3 dm.
Binkes sträcka består av 6 lodräta linjer och 5 vågräta med en total sträcka av 38 dm. Då de lodräta linjerna var för sig är 3dm så blir alla 6 tillsammans 3*6=18 dm och den sträcka som då återstår är 38-18=20 dm. Så en vågrät linje är 20/5=4 dm.
Banes sträcka består av 3 diagonaler till ett värde av 15 (3*5=15). 4 lodräta linjer till ett värde av 12 (4*3=12). 2 stycken vågräta till ett värde av 8 (4*2). Total längd är 15+12+8=35, så svaret är att Banes sträcka är 35 dm lång.

Svar: 8
Sabine har ritat det så här:
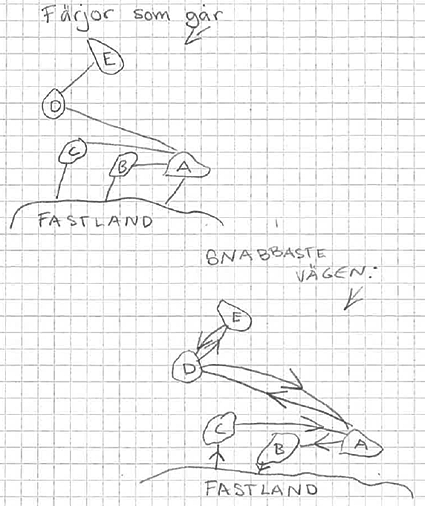
Helst ska man kolla kartan (och tidtabeller) när man planerar en resa men en turlista räcker för att lösa det här problemet.
Turlistan (trafikerade sträckor):
Fastlandet <--> A,
Fastlandet <--> B,
Fastlandet <--> C,
A <--> B,
A <--> C,
A <--> D,
D <--> E.
Då tar vi i tur och ordning:
Fastlandet ->B, B -> A, A -> D, D -> E, E -> D, D -> A, A -> C och C -> Fastlandet.
Man kan undra om det var nödvändigt med 8 överfarter. Skulle det inte gå med färre än så? Vi kan bevisa att det inte skulle gå.
Varje väg mellan E och fastlandet går via A och D, därför måste vi ta en färja till A och en färja till D minst 2 gånger: en gång på vägen till E och en gång på vägen tillbaka (4 överfarter). Dessutom måste vi åka minst en gång till B, C och E eftersom vi ska besöka dessa öar (3 överfarter) och minst en gång till fastlandet för att kunna komma hem (en överfart). Det blir minst 4+3+1=8 överfarter sammanlagt.
| problemen … Array |
lösningarna … Array |
Innehåll: LR
