
Svar: 8
Det har kommit in lösningar med två lite olika metoder:
Metod 1
Att match för match, beräkna antalet röda och antalet blåa kulor och summera röda och blåa efter sista matchen.
Sixten har 5 blåa och 5 röda. I första matchen förlorar han 2 röda och vinner 4 blåa. Då har han 3 röda och 9 blåa kvar. I andra matchen förlorar han 3 blåa och 1 röd. Då har han kvar 2 röda och 6 blåa kvar.
2+6=8 Svar: Han har 8 st kvar.
Inskickat av Carl i 6C på Kullaviksskolan.
Metod 2
Att först beräkna bara antalet röda kulor efter både matcherna, sedan göra samma sak med de blåa kulorna och sist summera antalet röda och blåa kulor.
röd: 5-2=3 3-1= 2
blå: 5+4= 9 9-3= 6
röd och blå: 2+6= 8
Inskickad av: Filippa M.
Metod 3
Man kan tänka sig också ett tredje sätt: Att match för match, se hur det sammanlagda antalet förändras.
första matchen: 10-2+4= 12 andra matchen: 12-3-1= 8.
Vi ses igen i adventskalendern!
Sixten
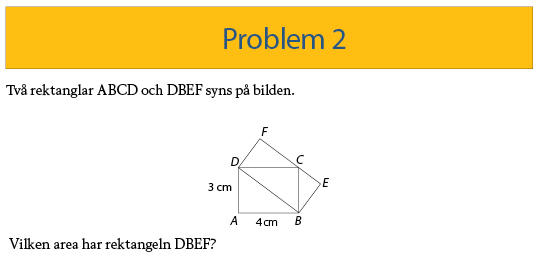
Svar: 12cm²
Problemet blev svårare än det var tänkt eftersom vi tappade måttet på sträckan AB vid hantering av figuren. Oskar och Ida på Fryxellskaskolan i Västerås klarade det ändå, jo nästan, genom att mäta sträckan AD i figuren, beräkna skalan och sedan mäta rektangeln DBEF och beräkna dess area.
Här kommer två lösningar till problemet så som det var tänkt:
Lösning 1
Pytagoras sats ger BD= 5. De rätvinkliga trianglarna BCD och DFC är likformiga. Det räcker att visa att ett par av de spetsiga vinklarna är lika i både trianglarna. Det gör vinklarna CBD och FDC, båda är lika med 90 – BDC. Då har vi proportionalitet DF/BC = CD/BD=4/5 och eftersom BC=3 så DF= 3 * 4/5 = 12/5.
Rektangeln DBEF har arean BD * DF = 5 * 12/5 = 12.
( Man kan, i stället för att beräkna DF visa likformighet mellan BCD och ECB och beräkna BE ).
Lösning 2
Att rektangeln ABCD har area 12cm² är lätt att se. Triangeln BCD är hälften så stor 6cm². Rektangeln DBEF har samma bas, BD, som triangeln BCD och samma höjd (mot basen BD) alltså dubbelt så stor area som triangeln, 12cm².
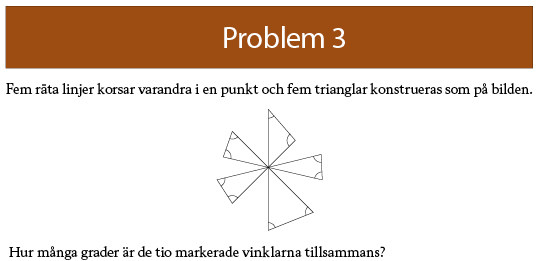
Svar: 720
Lösning 1
De 5 linjerna som korsar varandra i en punkt delar planet i 10 vinklar med sammanlagt storlek 360. 5 av dessa vinklar är trianglarnas omarkerade vinklar, övriga 5 är vertikalvinklar till de förra. Eftersom vertikalvinklar är lika stora så är också deras summor lika stora. Alltså summan av trianglarnas omarkerade vinklar och summan av deras vertikalvinklar (utanför trianglarna) är 180 var. Summan av alla trianglarnas alla vinklar är 5*180= 900. Summan av de markerade vinklarna är 900-180= 720.
Lösning 2
Tänk en myra som följer figurens linjer! När den kommer fram till en hörna med markerad vinkel svänger den. När den kommer fram till korsningspunkten fortsätter den rakt igenom.
När myran har gått alla de 15 sträckor, svängt i alla de 10 hörn och passerat korsningspunkten 10 gånger så passerar den startpunkten igen. Hur många varv runt sin egen axel har den svängt då? Låt den gå samma väg igen och se hur mycket den svänger! Det blir 3 varv eller i grader räknat 3*360= 1080 grader.
Låt oss nu se på detta från annan sida! När myran svänger i en hörna så svänger den 180 grader minus hörnans (markerade) vinkel. Sammanlagt i 10 hörn svänger den 1800 grader minus summan av de markerade vinklarna. Men vi vet ju redan att den svänger 1080 grader, alltså summan av de markerade vinklarna är 1800-1080=720 grader.
Lösning 3
Problem 3 är nu löst, på två sätt till och med. Kanske någon som vågar sig på en svårare variant?
De fem linjerna i figuren nedan korsar varandra inte i en utan i tio olika punkter, vad behöver man veta för att kunna bestämma summan av de markerade vinklarna?
Problemet kan behandlas i en praktisk övning. Elever ritar figuren på ett (av lokalvården godkänt) golv eller på asfalten eller markerar den med pålar och ett långt rep ute i naturen. En elev agerar myra, ett par mäter(*) de markerade vinklarna i myrans väg, en räknar och antecknar hur mycket myran svänger. Man summerar de markerade vinklarna, summerar myrans svängar och diskuterar hur de två summorna hänger ihop och varför.
(*) Har man inte tillgång till en precisionsvinkelmätare, så kan man använda ett långt och exakt måttband och en räknedosa med formelminne och en formel som bygger på cosinussatsen. Här följer en rutin för TI-30XIIB:
vinkelns korta ben [cm] STO A (uppdateras för varannan vinkel)
vinkelns långa ben [cm] STO B (uppdateras för varannan vinkel)
Avstånd mellan benens ändpunkter [cm] [ENTER]
cos^-1((A²+B²-Ans²)/2/A/B) [ENTER] (formeln återanvänds m h a uppåtpilen)
Innehåll: LR
