Svar och lösningar, okt 2010

Denna månad har vi fått lösningar från Dijana Avdagic.

I rutnätet ska det stå ett tal i varje ruta. Om du lägger samman talen i den övre raden blir summan 3. I den nedre raden är summan 8. Summan av talen i den vänstra kolumnen är 4. Vilken är summan i den högra kolumnen?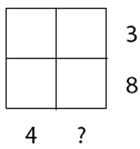

Lösning
7.
Vi försöker fylla i rutnätet. Vi skriver en etta och en tvåa i första raden så vi får summan 3. En trea under ettan ger summan 4 i första kolumnen och en femma sist ger summan 8 i andra raden. Då är summan av tal i andra kolumnen 2+5= 7. Nu vet vi att det går att fylla i rutnätet så att summorna stämmer och summan i andra kolumnen kan vara 7.
För att kunna säga om summan i andra kolumnen alltid är 7 eller om den ibland kan vara ett annat tal resonerar vi såhär:
Summan av talen i första raden ska vara 3, i andra raden 8, summan av alla tal i hela rutnätet 3+8= 11. Summan av talen i första kolumnen ska vara 4. I så fall måste summan av talen i den andra kolumnen vara 11-4 =7 om totalsumman är 11 i hela rutnätet.

Det tar 40 minuter för Mowgli att först gå till fots från sitt hem till havet och sedan direkt rida tillbaka hem på en elefant. Om han istället rider på elefanten till havet och direkt rider hem igen så tar det 32 minuter. Hur lång tid skulle det ta för honom att gå hela vägen till fots?

Lösning
48 min.
En lösning: Det tar 32 minuter att rida fram och tillbaka på en elefant, alltså 16 minuter i en riktning.
Att gå i en riktning och rida tillbaka tar 40 minuter, det betyder att det tar 40-16=24 minuter att gå
Att gå till havet och tillbaka tar 2*24=48 minuter.

En annan lösning: Mowgli sparar 8 minuter på att rida på en elefant hemifrån till havet jämfört med att gå till fots samma väg. Vi kan gissa att han sparar lika mycket på att rida elefant från havet hem jämfört med att gå, ungefär i alla fall, det är ju samma väg. Går han till fots både till havet och tillbaka så tar det 8 minuter längre än i det första fallet, alltså 48 minuter. Om Mowgli och hans elefanter finns i verkligheten så är detta sätt att tänka mera trovärdigt.
Man antar stillatigande att man rider respektive går i en riktning lika fort som i den andra, vilket brukar gälla i matematikproblemens idealiserade värld.

Vilket är det största möjliga antalet siffror i ett tal om varje par av siffror som står intill varandra ska bilda ett kvadrattal?

Lösning
5.
Om den första siffran är 1 så måste den andra vara 6 eftersom den enda tvåsiffriga kvadrat som börjar på 1 är 16. Är den andra siffran 6 så måste den tredje vara 4 eftersom den enda tvåsiffriga kvadrat som börjar på 6 är 64. Den fjärde siffran måste i så fall vara 9 och nu måste det vara slut eftersom det inte finns en tvåsiffrig kvadrat som börjar på 9. Det längsta talet som börjar på 1 och uppfyller problemets premiss är 1649. Alltså 4 siffror.
Testar vi tal som börjar på 2 på samma sätt så blir det två siffror som mest ”25”. Ingen tvåsiffrig kvadrat börjar på 5.
Fortsätter vi på samma sätt med tal som börjar med 3, 4, 5, 6, 7, 8 och 9 så får vi: 3649, 49, 5, 649, 7, 81649 och 9. Det längsta möjliga är alltså det femsiffriga 81649.
Ibland börjar vi skriva ett tal med 0, särskilt ett decimaltal. De kan vara hur långa som helst, tex
0.0000000000000000000000000000000000000000000000000016.